BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

I – BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bất phương trình bậc nhất hai ẩn $x,\,\,y$ có dạng tổng quát là

          $ax+by\le c\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)$                            

         $\left( ax+by<c;\,\,\,ax+by\ge c;\,\,\,ax+by>c \right)$

trong đó $a,\,\,b,\,\,c$ là những số thực đã cho, $a$ và $b$ không đồng thời bằng $0,\,\,x$ và $y$ là các ẩn số.

II – BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ $Oxy,$ tập hợp các điểm có tọa độ là nghiệm của bất phương trình $\left( 1 \right)$ được gọi là miền nghiệm của nó.

Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình $ax+by\le c$ như sau (tương tự cho bất phương trình $ax+by\ge c$)

Bước 1. Trên mặt phẳng tọa độ $Oxy,$ vẽ đường thẳng $\Delta $: $ax+by=c.$

Bước 2. Lấy một điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}} \right)$ không thuộc $\Delta $ (ta thường lấy gốc tọa độ $O$)

Bước 3. Tính $a{{x}_{0}}+b{{y}_{0}}$ và so sánh $a{{x}_{0}}+b{{y}_{0}}$ với $c.$

Bước 4. Kết luận

Nếu $a{{x}_{0}}+b{{y}_{0}}<c$ thì nửa mặt phẳng bờ $\Delta $ chứa ${{M}_{0}}$ là miền nghiệm của $a{{x}_{0}}+b{{y}_{0}}\le c.$

Nếu $a{{x}_{0}}+b{{y}_{0}}>c$ thì nửa mặt phẳng bờ $\Delta $ không chứa ${{M}_{0}}$ là miền nghiệm của $a{{x}_{0}}+b{{y}_{0}}\le c.$

Chú ý:

Miền nghiệm của bất phương trình $a{{x}_{0}}+b{{y}_{0}}\le c$ bỏ đi đường thẳng $ax+by=c$ là miền nghiệm của bất phương trình $a{{x}_{0}}+b{{y}_{0}}<c.$

Ví dụ.

Biểu diễn hình học tập nghiệm của bất phương trình $2x+y\le 3$

Giải

Vẽ đường thẳng $\Delta :2x+y=3.$

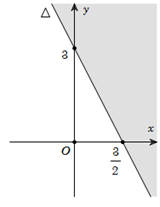
Lấy gốc tọa độ $O\left( 0;0 \right),$ ta thấy $O\notin \Delta $ và có $2.0+0<3$ nên nửa mặt phẳng bờ $\Delta $ chứa gốc tọa độ $O$ là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình).

III – HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Tương tự hệ bất phương trình một ẩn

Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn $x,\,\,y$ mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.

Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.

Ví dụ 1.

Biểu diễn hình học tập nghiệm của hệ bất phương trình:$\left\{ \begin{align}
& 3x+y\le 6 \\
& x+y\le 4 \\
& x\ge 0 \\
& y\ge 0 \\
\end{align} \right.$

Giải.

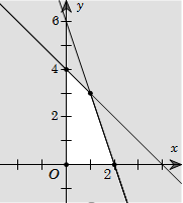
Vẽ các đường thẳng

$\begin{align}
& {{d}_{1}}:3x+y=6 \\
& {{d}_{2}}:x+y=4 \\
& {{d}_{2}}:x=0\,\,\,\,\,\,\left( Oy \right) \\
& {{d}_{2}}:y=0\,\,\,\,\,\,\left( Ox \right) \\
\end{align}$

Vì điểm ${{M}_{0}}\left( 1;1 \right)$ có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tô đậm các nửa mặt phẳng bờ $\left( {{d}_{1}} \right),$ $\left( {{d}_{2}} \right),$ $\left( {{d}_{3}} \right),$ $\left( {{d}_{4}} \right)$ không chứa điểm ${{M}_{0}}.$ Miền không bị tô đậm (hình tứ giác $OCIA$ kể cả bốn cạnh $AI,\,\,IC,\,\,CO,\,\,OA$) trong hình vẽ là miền nghiệm của hệ đã cho.

IV. VÍ DỤ MINH HỌA

Vấn đề 1. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1.

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

A. $2{{x}^{2}}+3y>0.$                       B. ${{x}^{2}}+{{y}^{2}}<2.$

C. $x+{{y}^{2}}\ge 0.$    D. $x+y\ge 0.$

Câu 2.

Cho bất phương trình $2x+3y-6\le 0\,\,(1)$. Chọn khẳng định đúng trong các khẳng định sau:

A. Bất phương trình $\left( 1 \right)$ chỉ có một nghiệm duy nhất.

B. Bất phương trình $\left( 1 \right)$vô nghiệm.

C. Bất phương trình $\left( 1 \right)$ luôn có vô số nghiệm.

D. Bất phương trình $\left( 1 \right)$có tập nghiệm là $\mathbb{R}$.

Câu 3.

Miền nghiệm của bất phương trình: $3x+2\left( y+3 \right)>4\left( x+1 \right)-y+3$ là nửa mặt phẳng chứa điểm:

A. $\left( 3;0 \right).$               B. $\left( 3;1 \right).$

C. $\left( 2;1 \right).$     D. $\left( 0;0 \right).$

Câu 4.

Miền nghiệm của bất phương trình: $3\left( x-1 \right)+4\left( \text{ }y-2 \right)<5x-3$ là nửa mặt phẳng chứa điểm:

A. $\left( 0;0 \right).$                         B. $\left( -4;2 \right).$

C. $\left( -2;2 \right).$ D. $\left( -5;3 \right).$

Câu 5.

Miền nghiệm của bất phương trình $-x+2+2\left( y-2 \right)<2\left( 1-x \right)$ là nửa mặt phẳng không chứa điểm nào trong các điểm sau?

A. $\left( 0;0 \right).$                         B. $\left( 1;1 \right).$

C. $\left( 4;2 \right).$     D. $\left( 1;-1 \right).$

Vấn đề 2. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1.

Cho hệ bất phương trình: $\left\{ \begin{align}
& x+3y-2\ge 0 \\
& 2x+y+1\le 0 \\
\end{align} \right.$.

Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

A. $M\left( 0;1 \right).$                       B. $N\left( 1;1 \right).$

C. $P\left( 1;3 \right).$ D. $Q\left( 1;0 \right).$

Câu 2.

Cho hệ bất phương trình: $\left\{ \begin{matrix}
2x-5y-1>0 \\
2x+y+5>0 \\
x+y+1<0 \\ \end{matrix} \right.$.

Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

A. $O\left( 0;0 \right).$                        B. $M\left( 1;0 \right).$

C. $N\left( 0;-2 \right).$            D. $P\left( 0;2 \right).$

Câu 3.

Miền nghiệm của hệ bất phương trình: $\left\{ \begin{align}
& \frac{x}{2}+\frac{y}{3}-1\ge 0 \\
& x\ge 0 \\
& x+\frac{1}{2}-\frac{3y}{2}\le 2 \\
\end{align} \right.$

chứa điểm nào trong các điểm sau đây?

A. $O\left( 0;0 \right).$                        B. $M\left( 2;1 \right).$

C. $N\left( 1;1 \right).$             D. $P\left( 5;1 \right).$

Câu 4.

Miền nghiệm của hệ bất phương trình: $\left\{ \begin{align}
& 3x+y\ge 9 \\
& x\ge y-3 \\
& 2y\ge 8-x \\
& y\le 6 \\
\end{align} \right.$

chứa điểm nào trong các điểm sau đây?

A. $O\left( 0;0 \right).$                        B. $M\left( 1;2 \right).$

C. $N\left( 2;1 \right).$             D. $P\left( 8;4 \right).$

Câu 5.

Điểm $M\left( 0;-3 \right)$ thuộc miền nghiệm của hệ bất phương trình nào sau đây?

A. $\left\{ \begin{align}
& 2x-y\le 3 \\
& 2x+5y\le 12x+8 \\
\end{align} \right..$

B. $\left\{ \begin{align}
& 2x-y>3 \\
& 2x+5y\le 12x+8 \\
\end{align} \right..$

C. $\left\{ \begin{align}
& 2x-y>-3 \\
& 2x+5y\le 12x+8 \\
\end{align} \right..$

D. $\left\{ \begin{align}
& 2x-y\le -3 \\
& 2x+5y\ge 12x+8 \\
\end{align} \right..$

Vấn đề 3. TÌM GTLN – GTNN CỦA BIỂU THỨC F(x,y) VỚI ĐIỀU KIỆN LÀ MỘT HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu 1.

Giá trị nhỏ nhất của biết thức $F=y-x$ trên miền xác định bởi hệ:

$\left\{ \begin{matrix}
y-2x\le 2 \\
2y-x\ge 4 \\
x+y\le 5 \\
\end{matrix} \right.$ là.

A. $\text{min }F=1$ khi $x=2,y=3$.                 

B. $\text{min }F=2$ khi $x=0,\text{ }y=2$.

C. $\text{min }F=3$ khi $x=1,y=4$.                 

D. $\text{min }F=0$ khi $x=0,\text{ }y=0$.

Câu 2.

Giá trị nhỏ nhất của biết thức $F=y-x$ trên miền xác định bởi hệ:

$\left\{ \begin{matrix}
2x+y\le 2 \\
x-y\le 2 \\
5x+y\ge -4 \\
\end{matrix} \right.$ là

A. $\text{min }F=-3$ khi $x=1,y=-2$.               

B. $\text{min}\,F=0$ khi$x=0,y=0$.

C. $\text{min }F=-2$ khi $x=\frac{4}{3},y=-\frac{2}{3}$.                  

D. $\text{min }F=8$ khi $x=-2,y=6$.

Câu 3

Cho hệ bất phương trình: $\left\{ \begin{align}
& x-y\le 2 \\
& 3x+5y\le 15 \\
& x\ge 0 \\
& y\ge 0 \\
\end{align} \right.$.

Khẳng định nào sau đây là khẳng định sai ?

A.Trên mặt phẳng tọa độ $Oxy$, biểu diễn miền nghiệm của hệbất phương trình đã cho là miền tứ giác $ABCO$ kể cả các cạnh với $A\left( 0;3 \right)$, $B\left( \frac{25}{8};\frac{9}{8} \right)$, $C\left( 2;0 \right)$ và $O\left( 0;0 \right)$.

B.Đường thẳng $\Delta :x+y=m$ có giao điểm với tứ giác $ABCO$ kể cả khi $-1\le m\le \frac{17}{4}$.

C.Giá trị lớn nhất của biểu thức $x+y$ , với $x$ và $y$ thỏa mãn hệ bất phương trình đã cho là $\frac{17}{4}$.

D.Giá trị nhỏ nhất của biểu thức $x+y$ , với $x$ và $y$ thõa mãn hệ bất phương trình đã cho là 0.

Câu 4.

Giá trị lớn nhất của biết thức $F\left( x;y \right)=x+2y$ với điều kiện: $\left\{ \begin{matrix}
0\le y\le 4 \\
x\ge 0 \\
x-y-1\le 0 \\
x+2y-10\le 0 \\
\end{matrix} \right.$ là

A. $6$.                            B. $8$.                          C. $10$.                        D. $12$.

Câu 5.

Giá trị nhỏ nhất của biết thức $F\left( x;y \right)=x-2y$ với điều kiện: $\left\{ \begin{matrix}
0\le y\le 5 \\
x\ge 0 \\
x+y-2\ge 0 \\
x-y-2\le 0 \\
\end{matrix} \right.$ là

A. $-10$.                         B. $12$.                        C. $-8$.                         D. $-6$.

Vấn đề 4. BÀI TOÁN KINH TẾ, BÀI TOÁN TỐI ƯU

Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức $T\left( x,y \right)=ax+by$ với $\left( x;y \right)$ nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước.

Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm $S$ là đa giác.

Bước 2: Tính giá trị của $F$ tương ứng với $\left( x;y \right)$ là tọa độ của các đỉnh của đa giác.

Bước 3: Kết luận:

$\bullet $ Giá trị lớn nhất của $F$ là số lớn nhất trong các giá trị tìm được.

$\bullet $ Giá trị nhỏ nhất của $F$ là số nhỏ nhất trong các giá trị tìm được.

Câu 1.

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo.

● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;

● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.

Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

A. $5$ lít nước cam và $4$ lít nước táo.                              B. $6$ lít nước cam và $5$ lít nước táo.    

C. $4$ lít nước cam và $5$ lít nước táo.                              D. $4$ lít nước cam và $6$ lít nước táo.    

Câu 2.

Một xưởng sản xuất hai loại sản phẩm

● Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;

● Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 nghìn.

Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?

A. $30$kg loại I và $40$ kg loại II.     B. $20$kg loại I và $40$ kg loại II.         

C. $30$kg loại I và $20$ kg loại II.     D. $25$kg loại I và $45$ kg loại II.        

Câu 3.

Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin $A$ và $B$ đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả $A$ lẫn $B$ và có thể tiếp nhận không quá 600 đơn vị vitamin $A$và không quá 500 đơn vị vitamin $B$. Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin $B$ không ít hơn một nửa số đơn vị vitamin $A$ và không nhiều hơn ba lần số đơn vị vitamin $A$. Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin $A$ có giá 9 đồng và mỗi đơn vị vitamin $B$ có giá 7,5 đồng.

A. $600$ đơn vị Vitamin $A$, $400$ đơn vị Vitamin $B.$

B. $600$ đơn vị Vitamin $A$, $300$ đơn vị Vitamin $B.$

C. $500$ đơn vị Vitamin $A$, $500$ đơn vị Vitamin $B.$

D. $100$ đơn vị Vitamin $A$, $300$ đơn vị Vitamin $B.$

Câu 4.

Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B₁, đựng cao Sao vàng và đựng “Quy sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.

$\bullet $ Cách thứ nhất cắt được 3 hộp B₁, một hộp cao Sao vàng và 6 hộp Quy sâm.

$\bullet $ Cách thứ hai cắt được 2 hộp B₁, 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B₁ tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?

A. Cắt theo cách một \[x-2<0\] tấm, cắt theo cách hai $300$ tấm.

B. Cắt theo cách một $150$ tấm, cắt theo cách hai $100$ tấm.

C. Cắt theo cách một $50$ tấm, cắt theo cách hai $300$ tấm.                             

D. Cắt theo cách một $100$ tấm, cắt theo cách hai $200$ tấm.

Câu 5.

Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm $A$ và sản phẩm $B$ trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm $A$ lãi $4$ triệu đồng người ta sử dụng máy $I$ trong $1$ giờ, máy $II$ trong $2$ giờ và máy $III$ trong $3$ giờ. Để sản xuất ra một tấn sản phẩm $B$ lãi được $3$ triệu đồng người ta sử dụng máy $I$ trong $6$ giờ, máy $II$ trong $3$ giờ và máy $III$ trong $2$ giờ. Biết rằng máy $I$ chỉ hoạt động không quá $36$ giờ, máy hai hoạt động không quá $23$ giờ và máy $III$ hoạt động không quá $27$ giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.

A. Sản xuất $9$ tấn sản phẩm $A$ và không sản xuất sản phẩm $B.$

B. Sản xuất $7$ tấn sản phẩm $A$ và $3$ tấn sản phẩm $B.$

C. Sản xuất $\frac{10}{3}$ tấn sản phẩm $A$ và $\frac{49}{9}$ tấn sản phẩm $B.$  

D. Sản xuất $6$ tấn sản phẩm $B$ và không sản xuất sản phẩm $A.$