CÁC PHÉP TOÁN SỐ PHỨC
Hãy thử sức với bài kiểm tra sau!
CHÚC CÁC BẠN HỌC TỐT!
Hướng dẫn và lời giải
Câu 1. (Mã 104 – 2020 Lần 2) Cho hai số phức ${{z}_{1}}=3-2i$ và ${{z}_{2}}=2+i$. Số phức ${{z}_{1}}-{{z}_{2}}$ bằng
A. $-1+3i$.
B. $-1-3i$.
C. $1+3i$.
D. $1-3i$.
Lời giải
Chọn D
Ta có ${{z}_{1}}-{{z}_{2}}=3-2i-\left( 2+i \right)=1-3i$
Câu 2. (Mã 103 – 2019) Cho hai số phức ${{z}_{1}}=1+i$ và ${{z}_{2}}=2+i$. Trên mặt phẳng tọa độ $Oxy$, điểm biểu diễn số phức ${{z}_{1}}+2{{z}_{2}}$có tọa độ là
A. $(3;5)$.
B. $(5;2)$.
C. $(5;3)$.
D. $(2;5)$.
Lời giải
Chọn C
Ta có ${{z}_{1}}+2{{z}_{2}}=(1+i)+2(2+i)=5+3i$.
Do đó điểm biểu diễn số phức ${{z}_{1}}+2{{z}_{2}}$có tọa độ là $(5;3)$.
Câu 3. (Mã 123 2017) Cho 2 số phức ${{z}_{1}}=5-7i$ và ${{z}_{2}}=2+3i$. Tìm số phức $z={{z}_{1}}+{{z}_{2}}$.
A. $z=3-10i$
B. $14$
C. $z=7-4i$
D. $z=2+5i$
Lời giải
Chọn C
$z=5-7i+2+3i=7-4i$.
Câu 4. (Đề Minh Họa 2017) Cho hai số phức ${{z}_{1}}=1+i$ và ${{z}_{2}}=2-3i$. Tính môđun của số phức${{z}_{1}}+{{z}_{2}}.$
A. $\left| {{z}_{1}}+{{z}_{2}} \right|=5$.
B. $\left| {{z}_{1}}+{{z}_{2}} \right|=\sqrt{5}$.
C. $\left| {{z}_{1}}+{{z}_{2}} \right|=1$.
D. $\left| {{z}_{1}}+{{z}_{2}} \right|=\sqrt{13}$.
Lời giải
Chọn D
${{z}_{1}}+{{z}_{2}}=1+i+\left( 2-3i \right)=3-2i$ nên ta có: $\left| {{z}_{1}}+{{z}_{2}} \right|=\left| 3-2i \right|=\sqrt{{{3}^{2}}+{{\left( -2 \right)}^{2}}}=\sqrt{13}$.
Câu 5. (Mã 110 2017) Cho hai số phức ${{z}_{1}}=4-3i$ và ${{z}_{2}}=7+3i$. Tìm số phức $z={{z}_{1}}-{{z}_{2}}$.
A. $z=-3-6i$
B. $z=11$
C. $z=-1-10i$
D. $z=3+6i$
Lời giải
Chọn A
Ta có $z={{z}_{1}}-{{z}_{2}}$$=\left( 4-3i \right)-\left( 7+3i \right)$$=-3-6i$.
Câu 6. (Mã 104 2017) Cho số phức ${{z}_{1}}=1-2i$, ${{z}_{2}}=-3+i$. Tìm điểm biểu diễn của số phức $z={{z}_{1}}+{{z}_{2}}$ trên mặt phẳng tọa độ.
A. $M\left( 2;-5 \right)$
B. $P\left( -2;-1 \right)$
C. $Q\left( -1;7 \right)$
D. $N\left( 4;-3 \right)$
Lời giải
Chọn B
$z={{z}_{1}}+{{z}_{2}}=-2-i$.
Câu 7. (Mã 104 2017) Tìm số phức $z$ thỏa mãn $z+2-3i=3-2i$.
A. $z=5-5i$
B. $z=1-i$
C. $z=1-5i$
D. $z=1+i$
Lời giải
Chọn D
$z+2-3i=3-2i$$\Leftrightarrow z=3-2i-2+3i=1+i$.
Câu 8. (Mã 105 2017) Cho hai số phức ${{z}_{1}}=1-3i$ và ${{z}_{2}}=-2-5i$. Tìm phần ảo $b$ của số phức $z={{z}_{1}}-{{z}_{2}}$.
A. $b=-3$
B. $b=2$
C. $b=-2$
D. $b=3$
Lời giải
Chọn B
Ta có $z={{z}_{1}}-{{z}_{2}}=3+2i\Rightarrow b=2$.
Câu 9. (Chuyen Phan Bội Châu Nghệ An 2019) Cho hai số phức ${{{z}_{1}}=1+i}$ và ${{{z}_{2}}=2-3i}$. Tính môđun của số phức ${{{z}_{1}}+{{z}_{2}}}$.
A. $\left| {{z}_{1}}+{{z}_{2}} \right|=1$. B. $\left| {{z}_{1}}+{{z}_{2}} \right|=\sqrt{5}$. C. $\left| {{z}_{1}}+{{z}_{2}} \right|=\sqrt{13}$. D. $\left| {{z}_{1}}+{{z}_{2}} \right|=5$.
Lời giải
Ta có ${{z}_{1}}+{{z}_{2}}=1+i+2-3i=3-2i\Rightarrow \left| {{z}_{1}}+{{z}_{2}} \right|=\left| 3-2i \right|=\sqrt{13}$.
Câu 10. (Đề Tham Khảo 2020 Lần 2) Cho hai số phức ${{z}_{1}}=3-i$ và ${{z}_{2}}=-1+i$. Phần ảo của số phức ${{z}_{1}}{{z}_{2}}$ bằng
A. $4$.
B. $4i$.
C. $-1$.
D. $-i$.
Lời giải
Chọn A
Ta có: ${{z}_{1}}{{z}_{2}}=\left( 3-i \right)\left( -1+i \right)=-2+4i$.
Suy ra phần ảo của ${{z}_{1}}{{z}_{2}}$ bằng $4$.
Câu 11. (Mã 101 – 2020 Lần 1) Cho hai số phức $z=1+2i$ và $\text{w}=3+i$. Môđun của số phức $z.\overline{\text{w}}$ bằng
A. $5\sqrt{2}$.
B. $\sqrt{26}$.
C. $26$.
D. $50$.
Lời giải
Chọn A.
Ta có $\left| z.\overline{\text{w}} \right|=\left| z \right|.\left| \overline{\text{w}} \right|=\left| z \right|.\left| \text{w} \right|=\sqrt{1+{{2}^{2}}}.\sqrt{{{3}^{2}}+1}=5\sqrt{2}.$
Câu 12. (Mã 103 – 2020 Lần 1) Cho hai số phức $z=4+2i$ và $w=1+i$. Môđun của số phức $z.\bar{w}$ bằng
A. $2\sqrt{2}.$
B. $8.$
C. $2\sqrt{10}.$
D. $40.$
Lời giải
Chọn C
Ta có: $z.\bar{w}=\left( 4+2i \right)\left( 1-i \right)=6-2i.$ Suy ra $\left| z.\bar{w} \right|=\sqrt{40}=2\sqrt{10}.$
Câu 13. (Mã 104 – 2020 Lần 1) Cho hai số phức $z=1+3i$ và $w=1+i$. Môđun của số phức $z.\bar{w}$ bằng
A. $2\sqrt{5}$.
B. $2\sqrt{2}$.
C. $20$.
D. $8$.
Lời giải
Chọn A
Ta có: $w=1+i\Rightarrow \bar{w}=1-i$
$z.\bar{w}=\left( 1+3i \right)\left( 1-i \right)=4+2i$
Từ đây ta suy ra: $\left| z.\bar{w} \right|=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5}$.
Câu 14. (Mã 102 – 2020 Lần 2) Cho số phức $z=2-i$, số phức $\left( 2-3i \right)\bar{z}$ bằng
A. $-1+8i$.
B. $-7+4i$.
C. $7-4i$.
D. $1+8i$.
Lời giải
Chọn C
Ta có: $\left( 2-3i \right)\bar{z}=\left( 2-3i \right)\left( 2+i \right)=7-4i$.
Câu 15. (Mã 103 – 2020 Lần 2) Cho số phức $z=-2+3i$, số phức $\left( 1+i \right)\bar{z}$ bằng
A. $-5-i$.
B. $-1+5i$.
C. $1-5i$.
D. $5-i$.
Lời giải
Chọn C
Ta có $z=-2+3i$ $\Rightarrow $ $\bar{z}=-2-3i$. Do đó $\left( 1+i \right)\bar{z}=\left( 1+i \right).\left( -2-3i \right)=1-5i$.
Câu 16. (Mã 104 – 2020 Lần 2) Cho số phức $z=-3+2i$, số phức $\left( 1-i \right)\overline{z}$ bằng
A. $-1-5i$
B. $5-i$.
C. $1-5i$.
D. $-5+i$.
Lời giải
Chọn D.
Vì $\overline{z}=-3-2i$ nên ta có $\left( 1-i \right)\overline{z}=(1-i)(-3-2i)=-5+i$
Câu 17. (Đề Minh Họa 2017) Cho số phức $z=2+5i.$ Tìm số phức $w=iz+\overline{z}$
A. $w=-3-3i$.
B. $w=3+7i.$.
C. $w=-7-7i$
D. $w=7-3i$.
Lời giải
Chọn A
Ta có $w=iz+\overline{z}=i(2+5i)+(2-5i)=2i-5+2-5i=-3-3i$
Câu 18. (Đề Tham Khảo 2017) Tính môđun của số phức $z$ biết $\bar{z}=\left( 4-3i \right)\left( 1+i \right)$.
A. $\left| z \right|=5\sqrt{2}$
B. $\left| z \right|=\sqrt{2}$
C. $\left| z \right|=25\sqrt{2}$
D. $\left| z \right|=7\sqrt{2}$
Lời giải
Chọn A
$\bar{z}=\left( 4-3i \right)\left( 1+i \right)$$=7+i$$\Rightarrow z=7-i$$\Rightarrow \left| z \right|=5\sqrt{2}$
Câu 19. (Mã 110 2017) Cho số phức $z=1-i+{{i}^{3}}$. Tìm phần thực $a$ và phần ảo $b$ của $z$.
A. $a=1,\,b=0$
B. $a=0,\,b=1$
C. $a=1,\,b=-2$
D. $a=-2,\,b=1$
Lời giải
Chọn C
Ta có: $z=1-i+{{i}^{3}}=1-i+{{i}^{2}}.i=1-i-i=1-2i$ (vì ${{i}^{2}}=-1$)
Suy ra phần thực của $z$ là $a=1$, phần ảo của $z$ là $b=-2$.
Câu 20. (Mã 123 2017) Cho số phước $z=1-2i.$ Điểm nào dưới đây là điểm biểu diễn số phức $w=iz$ trên mặt phẳng tọa độ
A. $Q\left( 1;2 \right)$
B. $N\left( 2;1 \right)$
C. $P\left( -2;1 \right)$
D. $M\left( 1;-2 \right)$
Lời giải
Chọn B
$w=iz=i\left( 1-2i \right)=2+i$
Câu 21. (Mã 101 – 2019) Cho hai số phức ${{z}_{1}}=1-i$ và ${{z}_{2}}=1+2i$. Trên mặt phẳng tọa độ $Oxy$, điểm biểu diễn số phức $3{{z}_{1}}+{{z}_{2}}$ có tọa độ là:
A. $\left( 1;4 \right)$.
B. $\left( -1;4 \right)$.
C. $\left( 4;1 \right)$.
D. $\left( 4;-1 \right)$.
Lời giải
Chọn D
$3{{z}_{1}}+{{z}_{2}}=3\left( 1-i \right)+\left( 1+2i \right)=4-i$. Suy ra: Tọa độ điểm biểu diễn là:$\left( 4;-1 \right).$
Câu 22. (Mã 102 – 2019) Cho hai số phức ${{z}_{1}}=-2+i$ và ${{z}_{2}}=1+i.$ Trên mặt phẳng tọa độ $Oxy,$ điểm biểu diễn số phức $2{{z}_{1}}+{{z}_{2}}$ có tọa độ là
A. $\left( -3;3 \right)$.
B. $\left( -3;2 \right)$.
C. $\left( 3;-3 \right)$.
D. $\left( 2;-3 \right)$.
Lời giải
Chọn A
Ta có: $2{{z}_{1}}+{{z}_{2}}=-4+2i+1+i=-3+3i.$
Vậy điểm biểu diễn số phức $2{{z}_{1}}+{{z}_{2}}$ có tọa độ là $\left( -3;3 \right)$.
Câu 23. Tìm số phức liên hợp của số phức $z=i\left( 3i+1 \right)$.
A. $\bar{z}=3+i$.
B. $\bar{z}=-3-i$.
C. $\bar{z}=3-i$.
D. $\bar{z}=-3+i$.
Lời giải
Chọn B
$z=i\left( 3i+1 \right)=-3+i$nên suy ra $\overline{z}=-3-i$.
Câu 24. (THPT Cẩm Giàng 2 2019) Cho số phức $z$thỏa mãn $z\left( 1+2i \right)=4-3i$. Tìm số phức liên hợp $\bar{z}$ của $z$.
A. $\bar{z}=\frac{-2}{5}-\frac{11}{5}i$.
B. $\text{\bar{z}}=\frac{\text{2}}{\text{5}}-\frac{\text{11}}{\text{5}}\text{i}$.
C. $\text{\bar{z}}=\frac{-2}{5}+\frac{11}{5}i$.
D. $\text{\bar{z}}=\frac{2}{5}+\frac{11}{5}i$.
Lời giải
Vì $z\left( 1+2i \right)=4-3i$ nên $z=\frac{4-3i}{1+2i}$$=\frac{\left( 4-3i \right)\left( 1-2i \right)}{{{1}^{2}}+{{2}^{2}}}$$=\frac{-2-11i}{5}$$=\frac{-2}{5}-\frac{11}{5}i$.
Vậy nên $\text{\bar{z}}=\frac{-2}{5}+\frac{11}{5}i$.
Câu 25. Cho số phức $z$ thỏa mãn $z\left( 1+i \right)=3-5i$. Tính môđun của $z$
A. $\left| z \right|=\sqrt{17}$.
B. $\left| z \right|=16$.
C. $\left| z \right|=17$.
D. $\left| z \right|=4$.
Lời giải
$z\left( 1+i \right)=3-5i\Leftrightarrow z=\frac{3-5i}{1+i}=-1-4i$$\Rightarrow \left| z \right|=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{17}$.
Câu 26. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho số phức $z={{\left( 1-2i \right)}^{2}}$. Tính mô đun của số phức $\frac{1}{z}$.
A. $\frac{1}{5}$.
B. $\sqrt{5}$.
C. $\frac{1}{25}$.
D. $\frac{1}{\sqrt{5}}$.
Lời giải
Ta có $z={{\left( 1-2i \right)}^{2}}=1-4i+4{{i}^{2}}=-3-4i$ $\Rightarrow \frac{1}{z}=\frac{1}{-3-4i}=-\frac{3}{25}+\frac{4}{25}i$.
Do đó $\left| \frac{1}{z} \right|=\sqrt{{{\left( -\frac{3}{25} \right)}^{2}}+{{\left( \frac{4}{25} \right)}^{2}}}=\frac{1}{5}$.
Câu 27. (KTNL GV Lý Thái Tổ 2019) Cho số phức $z={{\left( 1-i \right)}^{2}}\left( 1+2i \right)$. Số phức $z$có phần ảo là:
A. $2$.
B. $-2$.
C. $4$.
D. $-2i$.
Lời giải
Chọn B
Ta có: $z={{\left( 1-i \right)}^{2}}\left( 1+2i \right)=\left( 1-2i+{{i}^{2}} \right)\left( 1+2i \right)=-2i\left( 1+2i \right)=-2i-4{{i}^{2}}=4-2i$.
Suy ra số phức $z$có phần ảo là: $-2$.
Câu 28. (KTNL GV Thuận Thành 2 Bắc Ninh 2019) Cho số phức $z=1-\frac{1}{3}i$. Tìm số phức $\text{w}=i\overline{z}+3z$.
A. $\text{w}=\frac{8}{3}$.
B. $\text{w}=\frac{8}{3}+i$.
C. $\text{w}=\frac{10}{3}$.
D. $\text{w}=\frac{10}{3}+i$.
Lời giải
Chọn A
Ta có $z=1-\frac{1}{3}i\Rightarrow \overline{z}=1+\frac{1}{3}i$
Khi đó: $\text{w}=i\overline{z}+3z=i(1+\frac{1}{3}i)+3(1-\frac{1}{3}i)=\frac{8}{3}$
Câu 29. (THPT Yên Phong Số 1 Bắc Ninh 2019) Cho số phức $z=-2+i$. Điểm nào dưới đây là biểu diễn của số phức $w=iz$ trên mặt phẳng toạ độ?
A. $M\left( -1;-2 \right).$
B. $P\left( -2;1 \right).$
C. $N\left( 2;1 \right).$
D. $Q\left( 1;2 \right).$
Lời giải
Chọn A
Ta có: $w=iz=i\left( -2+i \right)=-1-2i$.
Vậy điểm biểu diễn số phức $w=iz$ là điểm $M\left( -1;-2 \right).$
Câu 30. (Chuyên Bắc Giang 2019) Cho số phức$z=1+2i$. Tìm tổng phần thực và phần ảo của số phức $w=2z+\overline{z}$.
A. $3$
B. $5$
C. $1$
D. $2$
Lời giải
Chọn B
Ta có $z=1+2i\Rightarrow \bar{z}=1-2i$
$w=2z+\overline{z}=2(1+2i)+1-2i=3+2i$
Vậy tổng phần thực và phần ảo của số phức $w$ là $5$
Câu 31. (Chuyên KHTN 2019) Cho số phức $z$ khác $0$. Khẳng định nào sau đây là sai?
A. $\frac{z}{{\bar{z}}}$là số thuần ảo.
B. $z.\bar{z}$ là số thực.
C. $z+\bar{z}$ là số thực.
D. $z-\bar{z}$là số ảo.
Lời giải
Đặt $z=a+bi,\text{ }\left( {{a}_{1}},{{b}_{1}}\in \mathbb{R} \right)\Rightarrow \bar{z}=a-bi$.
$\frac{z}{{\bar{z}}}=\frac{a+bi}{a-bi}=\frac{{{\left( a+bi \right)}^{2}}}{\left( a-bi \right)\left( a+bi \right)}=\frac{\left( {{a}^{2}}-{{b}^{2}} \right)+2ab.i}{{{a}^{2}}+{{b}^{2}}}=\frac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}+\frac{2ab}{{{a}^{2}}+{{b}^{2}}}.i$ chỉ là số thuần ảo
$\Leftrightarrow a=\pm b$.
Câu 32. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hai số phức ${{z}_{1}}=1+2i$ và ${{z}_{2}}=3-4i$. Số phức $2{{z}_{1}}+3{{z}_{2}}-{{z}_{1}}{{z}_{2}}$ là số phức nào sau đây?
A. $10i$.
B. $-10i$.
C. $11+8i$.
D. $11-10i$.
Lời giải
Ta có $2{{z}_{1}}+3{{z}_{2}}-{{z}_{1}}{{z}_{2}}$$=2\left( 1+2i \right)+3\left( 3-4i \right)-\left( 1+2i \right)\left( 3-4i \right)$$=11-8i-\left( 11+2i \right)=-10i$.
Câu 33. (THPT Gia Lộc Hải Dương Năm 2019) Tìm tọa độ điểm $M$ là điểm biểu diễn số phức $z$ biết $z$ thỏa mãn phương trình $\left( 1+i \right)\overline{z}=3-5i$.
A. $M\left( -1\,;\,4 \right)$.
B. $M\left( -1\,;\,-4 \right)$.
C. $M\left( 1\,;\,4 \right)$.
D. $M\left( 1\,;\,-4 \right)$.
Lời giải
Ta có $\left( 1+i \right)\overline{z}=3-5i$$\Leftrightarrow \overline{z}=\frac{3-5i}{1+i}$$\Leftrightarrow \overline{z}=-1-4i$.
Suy ra $z=-1+4i$. Vậy $M\left( -1\,;\,4 \right)$.
Câu 34. (Chuyên Lương Thế Vinh Đồng Nai 2019) Cho số phức $z$ thỏa mãn $\left( 1+3i \right)z-5=7i.$ Mệnh đề nào sau đây đúng?
A. $\overline{z}=\frac{13}{5}-\frac{4}{5}i$.
B. $\overline{z}=-\frac{13}{5}+\frac{4}{5}i$.
C. $\overline{z}=-\frac{13}{5}-\frac{4}{5}i$.
D. $\overline{z}=\frac{13}{5}+\frac{4}{5}i$.
Lời giải
$\left( 1+3i \right)z-5=7i\Leftrightarrow z=\frac{5+7i}{1+3i}\Leftrightarrow z=\frac{13}{5}-\frac{4}{5}i\Rightarrow \overline{z}=\frac{13}{5}+\frac{4}{5}i.$
Câu 35. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho số phức $z=\frac{\left( 2-3i \right)\left( 4-i \right)}{3+2i}$. Tìm tọa độ điểm biểu diễn của số phức $z$ trên mặt phẳng $Oxy$.
A. $\left( 1;\,4 \right)$.
B. $\left( -1;\,4 \right)$.
C. $\left( -1;\,-4 \right)$.
D. $\left( 1;\,-4 \right)$.
Lời giải
Ta có $z=\frac{\left( 2-3i \right)\left( 4-i \right)}{3+2i}$$=\frac{\left( 8-3 \right)-\left( 2+12 \right)i}{3+2i}$$=\frac{5-14i}{3+2i}$$=\frac{\left( 5-14i \right)\left( 3-2i \right)}{\left( 3+2i \right)\left( 3-2i \right)}$
$=\frac{\left( 15-28 \right)-\left( 10+42 \right)i}{9+4}$$=\frac{-13-52i}{13}$$=-1-4i$.
Vậy điểm biểu diễn số phức $z$trên mặt phẳng $Oxy$ là $M\left( -1;\,-4 \right)$.
Câu 36. (Chuyên Hạ Long 2019)Cho ${{z}_{1}}\,=\,2\,+\,4i,\,\,{{z}_{2}}\,=\,3\,-\,5i$. Xác định phần thực của $w\,=\,{{z}_{1}}.{{\overline{{{z}_{2}}}}^{2}}$
A. $-120$.
B. $-32$.
C. $88$.
D. $-152$.
Lời giải
Ta có $\,\overline{{{z}_{2}}}\,=\,3\,+\,5i\Rightarrow \,\,{{\overline{{{z}_{2}}}}^{2}}\,=\,-16\,+\,30i$$\,\Rightarrow \,w\,=\,{{z}_{1}}.{{\overline{{{z}_{2}}}}^{2}}\,=\,\left( 2\,+\,4i \right)\left( -16\,+\,30i \right)=\,-152\,-\,4i\,$.
Vậy phần thực của $w\,$là $-152$.
Câu 37. (Chuyên Bắc Giang 2019) Cho số phức z thỏa mãn phương trình $(3+2i)z+{{(2-i)}^{2}}=4+i$. Tìm tọa độ điểm M biểu diễn số phức z.
A. $M\left( -1;1 \right)$
B. $M\left( -1;-1 \right)$
C. $M\left( 1;1 \right)$
D. $M\left( 1;-1 \right)$
Lời giải
Chọn C
Ta có $z=\frac{4+i-{{\left( 2-i \right)}^{2}}}{3+2i}=1+i$ nên $M\left( 1;1 \right)$.
Câu 38. (Chuyên Đại Học Vinh 2019) Cho số phức $z$ thỏa mãn ${{\left( 1-\sqrt{3}i \right)}^{2}}z=4-3i$. Môđun của $z$ bằng
A. $\frac{5}{4}$
B. $\frac{5}{2}$
C. $\frac{2}{5}$
D. $\frac{4}{5}$
Lời giải
Chọn A
Ta có $z=\frac{4-3i}{{{\left( 1-\sqrt{3}i \right)}^{2}}}$$\Rightarrow \left| z \right|=\frac{\left| 4-3i \right|}{{{\left| 1-\sqrt{3}i \right|}^{2}}}=\frac{5}{4}$.
Câu 39. (THPT Ngô Quyền – Quảng Ninh – 2018) Cho $z=\frac{3+i}{x+i}$. Tổng phần thực và phần ảo của $z$ là
A. $$ $\frac{2x-4}{2}$.
B. $\frac{4x+2}{2}$.
C. $\frac{4x-2}{{{x}^{2}}+1}$.
D. $\frac{2x+6}{{{x}^{2}}+1}$.
Lời giải
Ta có: $z=\frac{3+i}{x+i}=\frac{\left( 3+i \right)\left( x-i \right)}{(x+i)(x-i)}=\frac{3x-3i+xi+1}{{{x}^{2}}+1}=\frac{3x+1}{{{x}^{2}}+1}+\frac{(x-3)i}{{{x}^{2}}+1}$.
Suy ra tổng phần thực và phần ảo của số phức $z$ là: $\frac{3x+1}{{{x}^{2}}+1}+\frac{x-3}{{{x}^{2}}+1}=\frac{4x-2}{{{x}^{2}}+1}$.
————————-
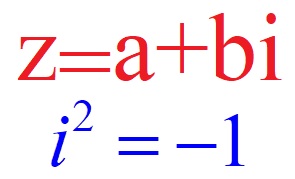


0 Bình luận