CÁC PHƯƠNG PHÁP GIẢI BẤT PHƯƠNG TRÌNH MŨ

BẤT PHƯƠNG TRÌNH MŨ

Dạng cơ bản

$\begin{array}{*{20}{c}} \bullet &{a > 1;{a^{u(x)}}} \end{array}\mathop \ge \limits_{\left( {\begin{array}{*{20}{c}} > \\ \le \\ < \end{array}} \right)} {a^{v(x)}} \Leftrightarrow u(x)\mathop \ge \limits_{\left( {\begin{array}{*{20}{c}} > \\ \le \\ < \end{array}} \right)} v(x)$

$\begin{array}{*{20}{c}} \bullet &{0 < a < 1;{a^{u(x)}}} \end{array}\mathop \ge \limits_{\left( {\begin{array}{*{20}{c}} > \\ \le \\ < \end{array}} \right)} {a^{v(x)}} \Leftrightarrow u(x)\mathop \le \limits_{\left( {\begin{array}{*{20}{c}} < \\ \ge \\ > \end{array}} \right)} v(x)$

Ví dụ:

Giải bpt: ${{2}^{{{x}^{2}}-2x}}\ge 8$

Hướng dẫn và lời giải

$BPT\Leftrightarrow {{2}^{{{x}^{2}}-2x}}\le {{2}^{3}}$$\Leftrightarrow {{x}^{2}}-2x\le 3$$\Leftrightarrow {{x}^{2}}-2x-3\le 0$$\Leftrightarrow -1\le x\le 3$

Ví dụ:

Giải bpt: ${{\left( \frac{2}{3} \right)}^{{{x}^{2}}-4x}}\ge \frac{8}{27}$

Hướng dẫn và lời giải

$BPT\Leftrightarrow {{\left( \frac{2}{3} \right)}^{{{x}^{2}}-4x}}\ge \frac{27}{8}={{\left( \frac{2}{3} \right)}^{-3}}$$\Leftrightarrow {{x}^{2}}-4x\le -3$$\Leftrightarrow {{x}^{2}}-4x+3\le 0$$\Leftrightarrow 1\le x\le 3$

B. Các phương pháp giải toán

1. Phương pháp biến đổi đưa về cùng cơ số

Ví dụ:

Giải bpt: ${{3}^{x}}-{{2}^{x+1}}\ge {{3}^{x+2}}-{{2}^{x+3}}$

Hướng dẫn và lời giải

$BPT\Leftrightarrow {{3}^{x}}+{{3}^{x+2}}\ge {{2}^{x+3}}+{{2}^{x+1}}$$\Leftrightarrow {{3}^{x}}+{{9.3}^{x}}\ge {{8.2}^{x}}+{{2.2}^{x}}$$\Leftrightarrow {{10.3}^{x}}\ge {{10.2}^{x}}$$\Leftrightarrow {{\left( \frac{3}{2} \right)}^{x}}\ge 1$$\Leftrightarrow {{\left( \frac{3}{2} \right)}^{x}}\ge 1={{\left( \frac{3}{2} \right)}^{0}}$$\Leftrightarrow x\ge 0.$

Bài tập

Giải các bất phương trình sau:

a) ${{3}^{x}}-{{5}^{x+1}}\ge {{3}^{x+2}}-{{5}^{x+3}}$

b) ${{3}^{{{x}^{2}}}}-{{2}^{{{x}^{2}}+1}}\ge {{3}^{{{x}^{2}}+2}}-{{2}^{{{x}^{2}}+3}}$

2. Phương pháp logarít hóa

Ví dụ:

Giải bpt: ${{2}^{{{x}^{2}}}}{{.3}^{x}}\ge 6.$

Hướng dẫn và lời giải

$BPT\Leftrightarrow \frac{{{2}^{{{x}^{2}}}}{{.3}^{x}}}{6}\ge 1$$\Leftrightarrow \frac{{{2}^{{{x}^{2}}}}{{.3}^{x}}}{2.3}\ge 1$$\Leftrightarrow {{2}^{{{x}^{2}}-1}}{{.3}^{x-1}}\ge 1$$\Leftrightarrow {{\log }_{2}}\left( {{2}^{{{x}^{2}}-1}}{{.3}^{x-1}} \right)\ge {{\log }_{2}}1$$\Leftrightarrow {{\log }_{2}}\left( {{2}^{{{x}^{2}}-1}} \right)+{{\log }_{2}}\left( {{3}^{x-1}} \right)\ge 0$$\Leftrightarrow {{x}^{2}}-1+\left( x-1 \right).{{\log }_{2}}3\ge 0$$\Leftrightarrow {{x}^{2}}+x.{{\log }_{2}}3-1-{{\log }_{2}}3\ge 0$

Do $a+b+c=1+{{\log }_{2}}3-1-{{\log }_{2}}3=0$.

$VT=0\Leftrightarrow x=1;x=-1-{{\log }_{2}}3$

Dấu vế trái

$x$	$-\infty $	$-1-{{\log }_{2}}3$		$-1$		$+\infty $
VT	+	0	–	0	+

Vậy BPT có nghiệm: $x\in \left( -\infty ;-1-{{\log }_{2}}3 \right]\cup \left[ 1;+\infty  \right).$

Bài tập

Giải các bất phương trình sau:

a) ${{3}^{{{x}^{2}}}}{{.4}^{x}}\ge 12.$

b) ${{3}^{{{x}^{2}}}}{{.5}^{x}}<1.$

c) ${{5}^{{{x}^{2}}}}{{.7}^{x}}\ge 245.$

3. Phương pháp đặt ẩn phụ loại 1.

Ví dụ:

Giải bpt: ${{4}^{x}}-{{5.2}^{x}}+4\le 0.$

Hướng dẫn và lời giải

$BPT\Leftrightarrow {{2}^{2x}}-{{5.2}^{x}}+4\ge 0.$

Đặt:$t={{2}^{x}}>0.$

 $BPT\Leftrightarrow {{t}^{2}}-5.t+4\le 0$$\Leftrightarrow 1\le t\le 4$$\Leftrightarrow 1\le {{2}^{x}}\le 4$$\Leftrightarrow 0\le x\le 2$

Bài tập

Giải bất phương trình sau:

a) ${{9}^{x}}-{{10.3}^{x}}+9\le 0.$

b) ${{2}^{2x+1}}-{{5.2}^{x}}+2>0.$

c) ${{6.9}^{x}}-{{13.6}^{x}}+{{6.4}^{x}}\le 0.$

4. Phương pháp đánh giá

Ví dụ 1:

Giải bất phương trình:${{4}^{x}}+{{5}^{x}}>9.(1)$

Hướng dẫn và lời giải

Ta có:

$\begin{array}{l} \begin{array}{*{20}{c}} \bullet &{\forall x > 1:\underline {\left\{ {\begin{array}{*{20}{c}} {{4^x} > {4^1} = 4}\\ {{5^x} > {5^1} = 5} \end{array}} \right.} } \end{array}\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}& \Rightarrow \end{array}}&{{4^x}} \end{array} + {5^x} > {4^1} + {5^1} = 9 \end{array}$

Suy ra $\forall x>1$ là một tập nghiệm của (1).

$\begin{array}{l} \begin{array}{*{20}{c}} \bullet &{\forall x \le 1:\underline {\left\{ {\begin{array}{*{20}{c}} {{4^x} \le {4^1} = 4}\\ {{5^x} \le {5^1} = 5} \end{array}} \right.} } \end{array}\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}& \Rightarrow \end{array}}&{{4^x}} \end{array} + {5^x} \le {4^1} + {5^1} = 9 \end{array}$

Suy ra $\forall x\le 1$ không là nghiệm của (1).

Vậy bất phương trình có tập nghiệm:$D=\left( 1;+\infty  \right)$.

Ví dụ 2:

Giải phương trình:${{3}^{x}}+{{4}^{x}}\le {{5}^{x}}.(2)$

Hướng dẫn và lời giải

Chia hai vế của phương trình cho ${{5}^{x}}>0.$Ta được: ${{\left( \frac{3}{5} \right)}^{x}}+{{\left( \frac{4}{5} \right)}^{x}}\le 1.$

Ta có:

$\begin{array}{l} \begin{array}{*{20}{c}} \bullet &{\forall x \ge 2:\underline {\left\{ {\begin{array}{*{20}{c}} {{{\left( {\frac{3}{5}} \right)}^x} \le {{\left( {\frac{3}{5}} \right)}^2} = \frac{9}{{25}}}\\ {{{\left( {\frac{4}{5}} \right)}^x} \le {{\left( {\frac{4}{5}} \right)}^2} = \frac{{16}}{{25}}} \end{array}} \right.} } \end{array}\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}& \Rightarrow \end{array}}&{{{\left( {\frac{3}{5}} \right)}^x} + {{\left( {\frac{4}{5}} \right)}^x} \le \frac{9}{{25}} + \frac{{16}}{{25}}} \end{array} = 1 \end{array}$

Suy ra $\forall x\ge 2$là một tập nghiệm của bấtphương trình (2).

$\begin{array}{l} \begin{array}{*{20}{c}} \bullet &{\forall x < 2:\underline {\left\{ {\begin{array}{*{20}{c}} {{{\left( {\frac{3}{5}} \right)}^x} > {{\left( {\frac{3}{5}} \right)}^2} = \frac{9}{{25}}}\\ {{{\left( {\frac{4}{5}} \right)}^x} > {{\left( {\frac{4}{5}} \right)}^2} = \frac{{16}}{{25}}} \end{array}} \right.} } \end{array}\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}& \Rightarrow \end{array}}&{{{\left( {\frac{3}{5}} \right)}^x} + {{\left( {\frac{4}{5}} \right)}^x} > \frac{9}{{25}} + \frac{{16}}{{25}}} \end{array} = 1 \end{array}$

Suy ra $\forall x<2$không là nghiệm của bấtphương trình (2).

Vậy bất phương trình đã cho có tập nghiệm: $x\ge 2.$

Bài tập

Giải các phương trình sau:

a)${{6}^{x}}+{{8}^{x}}<{{10}^{x}}$

b)${{5}^{x}}+{{12}^{x}}\ge {{13}^{x}}$

c)${{3}^{x+1}}+{{4}^{x+2}}>19$

d)${{2}^{x}}\le 3-x$

5. Phương pháp hàm

Loại 1. Giao của hai hàm số đơn điệu.

Các tính chất:

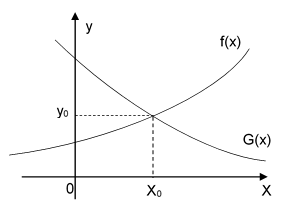
Tính chất 1: Nếu hàm $f\left( x \right)$tăng, $g\left( x \right)$giảm trên khoảng $\left( a;b \right)$ và$f\left( {{x}_{0}} \right)=g\left( {{x}_{0}} \right)$, ${{x}_{0}}\in \left( a;b \right)$thì phương trình $f\left( x \right)=g\left( x \right)$ có duy nhất nghiệm $x={{x}_{0}}$ và:

+ $f(x) \ge g(x) \Leftrightarrow x \ge {x_0}$

+ $f(x) < g(x) \Leftrightarrow x < {x_0}$

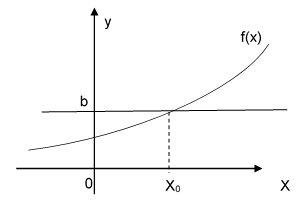
Hệ quả: Nếu $f'(x)>0$ với mọi $x\in K$ và tồn tại ${{x}_{0}}\in K$ sao cho: $f({{x}_{0}})=b$ thì phương trình $f(x)=b$ có nghiệm duy nhất ${{x}_{0}}$ thuộc $k$ và:

+ $f(x) \ge b \Leftrightarrow x \ge {x_0}$.

+ $f(x) < b \Leftrightarrow x < {x_0}$.

Dạng 1. Dạng $A.{{a}^{x}}+B.{{b}^{x}}\ge C.{{c}^{x}}$

Ví dụ 1:

Giải bất phương trình: ${{3}^{x}}+{{4}^{x}}\ge {{5}^{x}}$.

Hướng dẫn và lời giải

Chia hai vế cho ${{5}^{x}}>0$ta được: ${{\left( \frac{3}{5} \right)}^{x}}+{{\left( \frac{4}{5} \right)}^{x}}-1\ge 0$.

Đặt: $f(x)={{\left( \frac{3}{5} \right)}^{x}}+{{\left( \frac{4}{5} \right)}^{x}}-1$

Khi đó:$f'(x)={{\left( \frac{3}{5} \right)}^{x}}\ln \frac{3}{5}+{{\left( \frac{4}{5} \right)}^{x}}\ln \frac{4}{5}<0;\forall x\in \mathbb{R}$.

Suy ra hàm số $f(x)$luôn nghịch biến trên $\mathbb{R}$.

Mặt khác: $f(2)={{\left( \frac{3}{5} \right)}^{2}}+{{\left( \frac{4}{5} \right)}^{2}}-1=0.$

Do đó: Bất phương trình:$f(x)\ge 0\Leftrightarrow x\le 2.$

Vậy tập nghiệm của Bất phương trình đã cho là: $D=\left( -\infty ;2 \right]$.

Bài tập

Giải các bất phương trình sau:

a)${{6}^{x}}+{{8}^{x}}\le {{10}^{x}}$                   

b)${{5}^{x}}+{{12}^{x}}>{{13}^{x}}$                   

c) ${{4}^{x}}+3\ge {{7}^{x}}$

Dạng 2. Dạng $A.{{a}^{x}}\ge B.(b\text{x}+c)$

Ví dụ:

Giải bất phương trình: ${{3}^{x}}\ge 5-2x$.

Hướng dẫn và lời giải

Cách 1.

Đặt: $f(x)={{3}^{x}}=>f'(x)={{3}^{x}}\ln 3>0;\forall x\in \mathbb{R}.$

Hàm số $f(x)$đồng biến trên $\mathbb{R}$.

$g(x)=5-2\text{x}=>g'(x)=-2<0;\forall x\in \mathbb{R}.$

Hàm số $g(x)$nghịch biến trên $\mathbb{R}$.

Mặt khác: $f(1)=g(1)$.

Suy ra bất phương trình: $f(x)\ge g(x)\Leftrightarrow x\ge 1.$

Vậy tập nghiệm của BPT đã cho là: $D=\left[ 1;+\infty  \right)$.

Cách 2.

Bất Phương trình đã cho tương đương với:${{3}^{x}}+2\text{x}-5\ge 0.$

Đặt: $f(x)={{3}^{x}}+2\text{x}-5=>f'(x)={{3}^{x}}\ln 3+2>0;\forall x\in \mathbb{R}.$

Hàm số $f(x)$ đồng biến trên $\mathbb{R}$.

Mặt khác: $f(1)=0$.

Suy ra bất phương trình : $f(x)\ge 0\Leftrightarrow x\ge 1.$

Vậy tập nghiệm của BPT đã cho là: $D=\left[ 1;+\infty  \right)$.

Bài tập

Giải các phương trình sau:

a) ${{7}^{x-1}}\le 2-x$

b) ${{7}^{x}}>8-x$

2. Loại 2: Hàm đơn điệu.

Các tính chất

Tính chất 2: Nếu hàm $f~(x)$ tăng trên khoảng $\left( a;b \right)$ thì $\forall u,v\in \left( a,b \right)$ ta có:$f(u)\le f\left( v \right)\Leftrightarrow u\le v$.

Ví dụ 1.

Giải bất phương trình:$-{{2}^{{{x}^{2}}-x}}+{{2}^{x-1}}\ge {{(x-1)}^{2}}$.

Hướng dẫn và lời giải

Viết lại bất phương trình dưới dạng: ${{2}^{x-1}}+x-1\ge {{2}^{{{x}^{2}}-x}}+{{x}^{2}}-x$.

Xét hàm số: $f\left( t \right)={{2}^{t}}+t$

Có: $f\left( t \right)={{2}^{t}}\ln 2+1>0;\forall t$, Suy ra $f(t)$ là hàm đồng biến trên $\mathbb{R}.$

Do vậy: $f\left( x-1 \right)\ge f\left( {{x}^{2}}-x \right)\Leftrightarrow x-1\ge {{x}^{2}}-x$.

${{x}^{2}}-2x+1\le 0\Leftrightarrow x=1$.

Vậy bất phương trình có nghiệm duy nhất$x=1$.

6. Phương pháp nhóm nhân tử chung và kỹ thuật lập bảng

Các tính chất Nếu $a.b\ge 0\Leftrightarrow \left[ \begin{matrix} \left\{ \begin{matrix} a\ge 0 \\ b\ge 0 \\ \end{matrix} \right. \\ \left\{ \begin{matrix} a\le 0 \\ b\le 0 \\ \end{matrix} \right. \\ \end{matrix} \right.$

Ví dụ 1:

Giải phương trình: ${{2}^{{{x}^{2}}+x}}-{{4.2}^{{{x}^{2}}-x}}-{{2}^{2x}}+4\ge 0$

Lời giải

Ta có: ${{2}^{{{x}^{2}}+x}}-{{4.2}^{{{x}^{2}}-x}}-{{2}^{2x}}+4\ge 0$$\Leftrightarrow \left( {{2}^{{{x}^{2}}-x}}-1 \right).\left( {{2}^{2x}}-4 \right)\ge 0$

Cách 1.

$\begin{array}{l} VT = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{2^{{x^2} – x}} = 1}\\ {{2^{2{\rm{x}}}} = 4} \end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} – x = 0}\\ {2x = 2} \end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = 1} \end{array}} \right. \end{array}$

$x$	$-\infty $                0                                1                       $+\infty $
VT	–          0              +               0      +

Vậy bất phương trình đã cho có tập nghiệm: $D=\left[ 0;+\infty  \right)$.

Cách 2. Ta có:

Xét: ${{2}^{{{x}^{2}}-x}}-1>0\Leftrightarrow {{2}^{{{x}^{2}}-x}}>1\Leftrightarrow {{x}^{2}}-x>0\Leftrightarrow \left[ \begin{matrix} x>1 \\ x<0 \\ \end{matrix} \right.$.

Xét: ${{2}^{2\text{x}}}-4>0\Leftrightarrow {{2}^{2\text{x}}}>4\Leftrightarrow 2\text{x}2\Leftrightarrow x>1.$
Từ đó ta có bảng dấu vế trái như sau:

Từ đó ta có bảng dấu vế trái như sau:

$x$	$-\infty $                0                               1                       $+\infty $
${{2}^{{{x}^{2}}-x}}-1$	+        0             –                0         +
${{2}^{2\text{x}}}-4$	–         |              –               0         +
VT	–        0              +              0         +

Vậy bất phương trình đã cho có tập nghiệm: $D=\left[ 0;+\infty  \right)$.

Bài tập: Giải các phương trình sau

1. _{${{6}^{x}}-{{3}^{x}}-{{2}^{x+1}}-2\ge 0$}                                                                    

b)${{x}^{2}}{{.2}^{x}}+\text{ }4x+\text{ }8\text{ }\ge \text{ }4.{{x}^{2}}+x{{.2}^{x}}+\text{ }{{2}^{x}}^{+\text{ }1}$

c) ${{18}^{x}}-{{9}^{x}}-{{2.6}^{x}}+{{2.3}^{x}}-{{3.2}^{x}}+3\le 0$                                   

d) $8\text{ }-x{{.2}^{x}}+\text{ }{{2}^{3\text{ }-\text{ }x}}-\text{ }x\text{ }\ge \text{ }0$

7. Phương pháp đặt ẩn phụ loại 2

+ Đưa một phần biến cũ theo biến mới

+ Đặt ẩn phụ không hoàn toàn.

Ví dụ 1: 

Giải bất phương trình: ${{9}^{x}}+2(x-2){{3}^{x}}+2x-5\ge 0$.

Hướng dẫn và lời giải

Đặt $t=\text{ }{{3}^{x}}>0$(*), khi đó ta có: ${{t}^{2}}+2\left( x-2 \right)t+2x-5\ge 0$.(**)

Có $a-b+c=1-2\left( x-2 \right)+2x-5=0$

$VT=0\Leftrightarrow t=-1;t=5-2x$ Khi đó bất phương trình (**)

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {t > 0}\\ {\left[ {\begin{array}{*{20}{c}} {t \le – 1}\\ {t \ge 5 – 2{\rm{x}}} \end{array}} \right.} \end{array}} \right. \Leftrightarrow t \ge 5 – 2{\rm{x}} \Leftrightarrow {3^x} \ge 5 – 2{\rm{x}} \Leftrightarrow {3^x} + 2{\rm{x – 5}} \ge 0.$

Đặt $f(x)={{3}^{x}}+2\text{x-5}=>f'(x)={{3}^{x}}\ln 3+2>0;\forall x$

Suy ra $f(x)$đồng biến trên $\mathbb{R}$.

Mặt khác $f(1)=0$, nên bất phương trình $f(x)\ge 0\Leftrightarrow x\ge 1.$

Vậy BPT đã cho có nghiệm có tập nghiệm: $D=\left[ 1;+\infty  \right).$

Lưu ý: Phương pháp này chỉ sử dụng khi D là số chính phương.

Bài tập:

a) Giải bất phương trình: ${{4}^{x}}+\left( x-5 \right){{.2}^{x}}-2x+6\le 0$

b) Giải bất phương trình: ${{9}^{x}}+\left( 5x+2 \right){{.3}^{x}}+15x-3\ge 0.$

————————————–

Xem thêm: Phương trình mũ.

————————————–