Các phương pháp xác định và tính Góc giữa hai đường thẳng trong không gian.

A. Kiến thức cốt lõi

Phương pháp 1. Phương pháp sử dụng định nghĩa

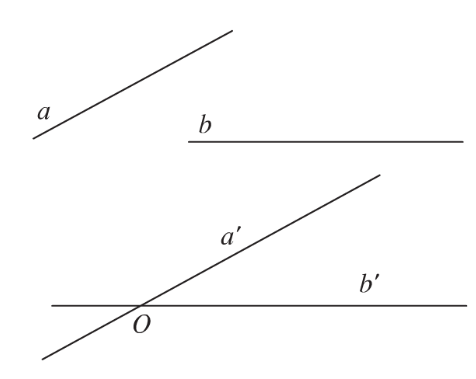
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm bất kì lần lượt song song với a và b.

Phương pháp 2. Phương pháp vec tơ

Cho  đường thẳng a có vec tơ chỉ phương ${\overrightarrow u }$; đường thẳng b có véc tơ chỉ phương ${\overrightarrow v }$ , khi đó:$\cos \left( {a,b} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow v } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow v } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}$

Phương pháp 3. Phương pháp tọa độ

Lập hệ trục tọa độ. Xác định góc giữa hai vec tơ bằng phương pháp tọa độ.

2. Ví dụ minh họa

Ví dụ 1. Cho tứ diện OABC, có OA, OB,OC đôi một vuông góc, OA=OB=OC=1. M là trung điểm của AB. Tính góc giữa OM và BC.

Giải

Cách 1. (Phương pháp định nghĩa).

Gọi D là trung điểm AC, suy ra MD//BC suy ra: $\widehat {\left( {OM,BC} \right)} = \widehat {(OM,MD)}.$ (1)

Xét tam giác OAB vuông cân tại O, cạnh OA=OB=1 nên $AB =AC=BC \sqrt 2 $ , mặt khác OM là trung tuyến nên $OM = \frac{1}{2}AB = \frac{{\sqrt 2 }}{2}$.

Tương tự $OD = \frac{1}{2}AC = \frac{{\sqrt 2 }}{2}$.

Tam giác ABC có MD là đường trung bình, nên $MD = \frac{1}{2}BC = \frac{{\sqrt 2 }}{2}$.

Xét tam giác OMD có $OM = OD = MD = \frac{{\sqrt 2 }}{2}$, nên tam giác OMD đều, suy ra góc $\widehat {OMD} = {60^0}$ (2).

Từ (1) và (2) Suy ra: $\widehat {\left( {OM,BC} \right)} = \widehat {(OM,MD)} = \widehat {OMD} = {60^0}$.

Cách 2. (Phương pháp vec tơ)

Ta có: $\cos \left( {OM,BC} \right) = \left| {\cos \left( {\overrightarrow {OM} ,\overrightarrow {BC} } \right)} \right| = \frac{{\left| {\overrightarrow {OM} .\overrightarrow {BC} } \right|}}{{\left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {BC} } \right|}}$

Dễ thấy: $\left\{ {\begin{array}{*{20}{c}} {OM = \frac{{\sqrt 2 }}{2}}\\ {BC = \sqrt 2 } \end{array}} \right.$

Suy ra: ${\left| {\overrightarrow {OM} } \right| = \frac{{\sqrt 2 }}{2}}$; ${\left| {\overrightarrow {BC} } \right| = \sqrt 2 }$.

Mặt khác: $\overrightarrow {OM} .\overrightarrow {BC} = \overrightarrow {OM} .\left( {\overrightarrow {BO} + \overrightarrow {OC} } \right)$ $ = \overrightarrow {OM} .\overrightarrow {BO} + \overrightarrow {OM} .\overrightarrow {OC} = \overrightarrow {OM} .\overrightarrow {BO} $ (Vì $OM \bot OC \Rightarrow \overrightarrow {OM} .\overrightarrow {OC} = 0$).

Ta lại có: $\overrightarrow {OM} .\overrightarrow {BO} = \left| {\overrightarrow {OM} } \right|\left| {\overrightarrow {BO} } \right|\cos \left( {\overrightarrow {OM} ,\overrightarrow {BO} } \right)$ $ = \frac{{\sqrt 2 }}{2}.1.\cos {135^0} = – \frac{1}{2}$

Vậy: $\cos \left( {OM,BC} \right) = \frac{1}{2}$ $ \Rightarrow \widehat {\left( {OM,BC} \right)} = {60^0}$.

Cách 3. Phương pháp tọa độ.

Lập hệ trục tọa độ (như hình vẽ).

Ta xác định được tọa độ của các điểm: $O(0;0;0);A(1;0;0);B(0;1;0);C(0;0;1).$

Do M là trung điểm AB Suy ra tọa độ điểm $M\left( {\frac{1}{2};\frac{1}{2};0} \right)$.

Có: $\overrightarrow {OM} = \left( {\frac{1}{2};\frac{1}{2};0} \right);\overrightarrow {BC} = \left( {0;1; – 1} \right)$ $ \Rightarrow \overrightarrow {OM} .\overrightarrow {BC} = \frac{1}{2}$

• $\left| {\overrightarrow {OM} } \right| = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2} + 0} = \frac{{\sqrt 2 }}{2}$
• $\left| {\overrightarrow {BC} } \right| = \sqrt {0 + {1^2} + {{( – 1)}^2}} = \sqrt 2 $

Ta có: $\cos \left( {OM,BC} \right) = \left| {\cos \left( {\overrightarrow {OM} ,\overrightarrow {BC} } \right)} \right| = \frac{{\left| {\overrightarrow {OM} .\overrightarrow {BC} } \right|}}{{\left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{1}{2}$

Vậy suy ra: $\left( {OM,BC} \right) = {60^0}$.

Ví dụ 2: Cho tứ diện $ABCD$ có $AB=2,AC=3,AD=BC=4,BD=2\sqrt{5},CD=5.$ Tính cosin góc giữa hai đường thẳng $AC$ và $BD.$

Lời giải: Ta có $\cos \left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {BD} }}{{AC.BD}}$ $ = \frac{{\overrightarrow {AC} \left( {\overrightarrow {AD} – \overrightarrow {AB} } \right)}}{{AC.BD}}$ $ = \frac{{\overrightarrow {AC} .\overrightarrow {AD} – \overrightarrow {AC} .\overrightarrow {AB} }}{{AC.BD}}$ $ = \frac{{\frac{{A{C^2} + A{D^2} – C{D^2}}}{2} – \frac{{A{C^2} + A{B^2} – B{C^2}}}{2}}}{{AC.BD}}$ $ = \frac{{A{D^2} + B{C^2} – C{D^2} – A{B^2}}}{{2AC.BD}}$ $ = \frac{{{4^2} + {4^2} – {5^2} – {2^2}}}{{2.3.2\sqrt 5 }} = \frac{1}{{4\sqrt 5 }}.$

Chọn đáp án A.

Ví dụ 3. Cho hình chóp S.ABC có $SA = SB = SC = AB = AC = a$, BC=$a\sqrt 2 $. Tính góc giữa hai đường thẳng AB và SC.

Giải

Ta có: $\cos \left( {AB,SC} \right) = \left| {\cos \left( {\overrightarrow {AB} ,\overrightarrow {SC} } \right)} \right| = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {SC} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {SC} } \right|}}$

Xét tam giác ABC có $A{C^2} + A{B^2} = 2{a^2} = B{C^2}$ $ \Rightarrow \Delta ABC$ vuông tại A.

Mặt khác: $\overrightarrow {AB} .\overrightarrow {SC} = \overrightarrow {AB} \left( {\overrightarrow {SA} + \overrightarrow {AC} } \right)$ $ = \overrightarrow {AB} .\overrightarrow {SA} + \overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} .\overrightarrow {SA} $

(Vì $\overrightarrow {AB} \bot \overrightarrow {AC} \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0$).

$ = \left| {\overrightarrow {AB} } \right|\left| {\overrightarrow {SA} } \right|\cos \left( {\overrightarrow {AB} ,\overrightarrow {SA} } \right) = a.a.\cos {60^0}$ $ = \frac{{{a^2}}}{2}$ (do tam giác SAB đều).

do đó: $\cos \left( {AB,SC} \right) = \left| {\cos \left( {\overrightarrow {AB} ,\overrightarrow {SC} } \right)} \right|$ $ = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {SC} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {SC} } \right|}} = \frac{{\frac{{{a^2}}}{2}}}{{a.a}} = \frac{1}{2}$

suy ra: $\left( {AB,SC} \right) = {60^0}$

Vậy chọn đáp án B.

3. Bài tập vận dụng

Bài 1. Cho hình chóp $S.ABCD$ có tất cả các cạnh đều bằng$~a$ . Gọi $I$ và $J$ lần lượt là trung điểm của $SC$ và $BC$. Số đo của góc $\left( \text{ }IJ,\text{ }CD \right)$ bằng:

A. $90{}^\circ $.           B. $45{}^\circ $.                     C. $30{}^\circ $.            D. $60{}^\circ $.

Bài 2. Cho tứ diện $ABCD$ đều cạnh bằng $a$. Gọi $M$ là trung điểm $CD$, $\alpha $ là góc giữa $AC$ và $BM$. Chọn khẳng định đúng?

A. $\cos \alpha = \frac{{\sqrt 3 }}{4}$

B. $\cos \alpha = \frac{1}{{\sqrt 3 }}$

C. $\cos \alpha = \frac{{\sqrt 3 }}{6}$

D. $\cos \alpha = \frac{1}{2}$

Bài 3. Cho hình lập phương $ABCD.EFGH$. Hãy xác định góc giữa cặp vectơ $\overrightarrow{AF}$ và $\overrightarrow{EG}$?

A. $90{}^\circ $                B. $60{}^\circ $                C. $45{}^\circ $             D. $120{}^\circ $

Bài 4. Cho hình lập phương $ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$. Góc giữa $AC$ và $D{{A}_{1}}$ là

A. $45{}^\circ $.              B. $90{}^\circ $.            C. $60{}^\circ $.            D. $120{}^\circ $.

Bài 5. Cho tứ diện đều $ABCD$, $M$ là trung điểm của cạnh $BC$. Khi đó $\cos \left( AB,DM \right)$ bằng

A.$\frac{\sqrt{2}}{2}$.         B. $\frac{\sqrt{3}}{6}$.        C. $\frac{1}{2}$.        D. $\frac{\sqrt{3}}{2}$.

4. Tài liệu đính kèm

Xem thêm:

• Góc giữa hai đường thẳng.
• Tọa độ vec tơ trong không gian.