Bài viết mới Chủ đề 3. Giá trị lớn nhất, Nhỏ nhất của hàm số
389: Phương pháp giải toán trắc nghiệm GTLN-GTNN (Max-Min) của hàm số.
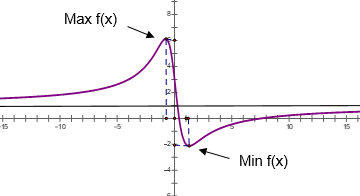
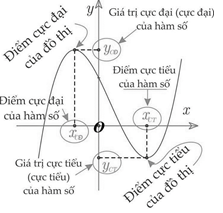
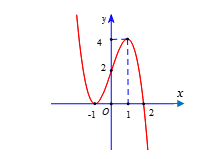
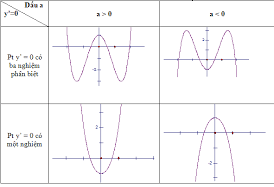
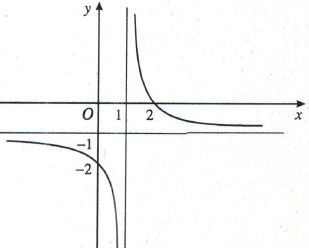
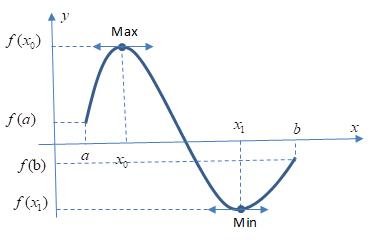
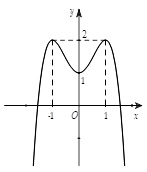
Phần 1. GTLN-GTNN của hàm số không tham số Dạng 1. Tìm Max-Min khi biết đồ thị hàm số Ví dụ 1. Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -1;3 \right]$ và có đồ thị như hình vẽ bên. Gọi $M$ và $m$ lần lượt là Đọc tiếp…