Đề 001-TN THPT QG

Đề 001-TN THPT QG

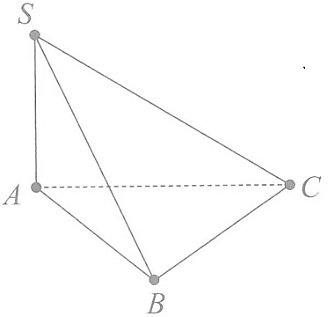
Câu 36. Cho hình chóp S.ABC có SA vuông góc với mặt phẳng $\left( ABC \right),$$SA=2a,$ tam giác ABC vuông tại B, $AB=a\sqrt{3}$ và $BC=a$(minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng $\left( ABC \right)$ bằng

A. $90{}^\circ .$           

B. $45{}^\circ .$

C. $30{}^\circ .$           

D. $60{}^\circ .$

Hướng dẫn giải

Đáp án B

Ta có $SA\bot \left( ABC \right)$ nên AC là hình chiếu của SC lên mặt phẳng $\left( ABC \right).$ Do đó $\left( SC,\left( ABC \right) \right)=\left( SC,AC \right)=\widehat{SCA}.$ Tam giác ABC vuông tại B, $AB=a\sqrt{3}$ và $BC=a$ nên $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{4{{a}^{2}}}=2a.$ Do đó tam giác SAC vuông cân tại A nên $\widehat{SCA}=45{}^\circ .$ Vậy $\left( SC,\left( ABC \right) \right)=45{}^\circ .$

Trở lại đề thi