Đề 001-TN THPT QG

Đề 001-TN THPT QG

Câu 40. Cho hàm số $y=f\left( x \right)$ có đạo hàm ${f}’\left( x \right)$. Đồ thị của hàm số $y={f}’\left( x \right)$ như hình vẽ.

Giá trị lớn nhất của hàm số $g\left( x \right)=f\left( 3x \right)+9x$ trên đoạn $\left[ -\frac{1}{3};\frac{1}{3} \right]$ là

A. $f\left( 1 \right)$       

B. $f\left( 1 \right)+2$

C. $f\left( \frac{1}{3} \right)$

D. $f\left( 0 \right)$

Hướng dẫn giải

Chọn D

Đặt $t=3x$ thì $t\in \left[ -1;1 \right]$ và ta đưa về xét $g\left( t \right)=f\left( t \right)+3t$

Ta có

$\begin{array}{l} g’\left( t \right) = f’\left( t \right) + 3 = 0\\ \Leftrightarrow f’\left( t \right) = – 3\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {{t_1} = – 1}\\ {{t_2} = 0}\\ {{t_3} = 1}\\ {{t_4} = 2} \end{array}} \right. \end{array}$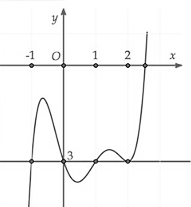

Vẽ BBT cho ${g}’\left( t \right)$ trên $\left[ -1;1 \right]$, ta thấy trong đoạn $\left[ -1;1 \right]$, hàm số ${g}’\left( t \right)$ đổi dấu từ $+$ sang $-$ qua ${{t}_{2}}=0$, vậy giá trị lớn nhất của hàm số là $g\left( 0 \right)=f\left( 0 \right)+0$.

Trở về đề thi