Đề 001-TN THPT QG

Đề 001-TN THPT QG

Câu 46. Cho số phức ${{z}_{1}}$, ${{z}_{2}}$ thỏa mãn $\left| {{z}_{1}} \right|=12$ và $\left| {{z}_{2}}-3-4\text{i} \right|=5$. Giá trị nhỏ nhất của $\left| {{z}_{1}}-{{z}_{2}} \right|$ là:

A. $0$.                            B. $2$                           C. $7$                           D. $17$

Hướng dẫn giải

Chọn B

Gọi ${{z}_{1}}={{x}_{1}}+{{y}_{1}}\text{i}$ và ${{z}_{2}}={{x}_{2}}+{{y}_{2}}\text{i}$, trong đó ${{x}_{1}}$, ${{y}_{1}}$, ${{x}_{2}}$, ${{y}_{2}}$$\in \mathbb{R}$; đồng thời ${{M}_{1}}\left( {{x}_{1}};{{y}_{1}} \right)$ và ${{M}_{2}}\left( {{x}_{2}};{{y}_{2}} \right)$ lần lượt là điểm biểu diễn các số phức ${{z}_{1}}$, ${{z}_{2}}$.

Theo giả thiết, ta có:

$\left\{ \begin{align} & x_{1}^{2}+y_{1}^{2}=144 \\ & {{\left( {{x}_{2}}-3 \right)}^{2}}+{{\left( {{y}_{2}}-4 \right)}^{2}}=25 \\ \end{align} \right.$.

Do đó ${{M}_{1}}$ thuộc đường tròn $\left( {{C}_{1}} \right)$ có tâm $O\left( 0;0 \right)$ và bán kính ${{R}_{1}}=12$, ${{M}_{2}}$ thuộc đường tròn $\left( {{C}_{2}} \right)$ có tâm $I\left( 3;4 \right)$ và bán kính ${{R}_{2}}=5$.

Mặt khác, ta có

$\left\{ \begin{align} & O\in \left( {{C}_{2}} \right) \\ & OI=5<7={{R}_{1}}-{{R}_{2}} \\ \end{align} \right.$

nên $\left( {{C}_{2}} \right)$ chứa trong $\left( {{C}_{1}} \right)$.

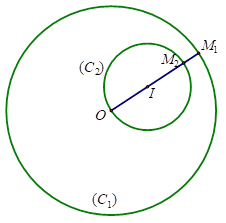
Khi đó $\left| {{z}_{1}}-{{z}_{2}} \right|$$={{M}_{1}}{{M}_{2}}$. Suy ra ${{\left| {{z}_{1}}-{{z}_{2}} \right|}_{\min }}\Leftrightarrow {{\left( {{M}_{1}}{{M}_{2}} \right)}_{\min }}$$\Leftrightarrow {{M}_{1}}{{M}_{2}}={{R}_{1}}-2{{R}_{2}}=2$.

Trở về đề thi