Câu 49. Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ có $f\left( 0 \right)=1$ và đồ thị hàm số $y=f’\left( x \right)$ như hình vẽ bên. Hàm số $y=\left| f\left( 3x \right)-9{{x}^{3}}-1 \right|$ đồng biến trên khoảng:
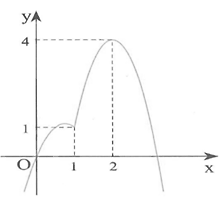
A. $\left( \frac{1}{3};+\infty \right)$
B. $\left( -\infty ;0 \right)$
C. $\left( 0;2 \right)$
D. $\left( 0;\frac{2}{3} \right)$
Hướng dẫn giải
Đáp án D
Đặt
$\begin{array}{l} g\left( x \right) = f\left( {3x} \right) – 9{x^3} – 1\\ \Rightarrow g’\left( x \right) = 3f’\left( {3x} \right) – 27{x^2}\\ g’\left( x \right) = 0 \Leftrightarrow f’\left( {3x} \right) = {\left( {3x} \right)^2}\left( * \right) \end{array}$Trên cùng một mặt phẳng tọa độ, ta vẽ đồ thị hàm số $y=f’\left( x \right)$ và $y={{x}^{2}}$ như hình vẽ.
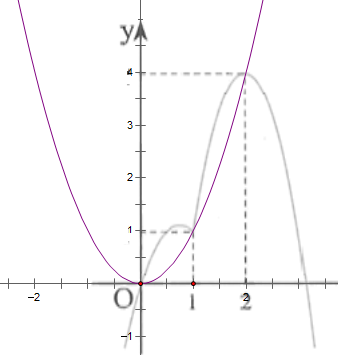
Từ đồ thị hàm số ta có:
$\left( * \right) \Leftrightarrow \left[ \begin{array}{l} 3x = 0\\ 3x = 1\\ 3x = 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \frac{1}{3}\\ x = \frac{2}{3} \end{array} \right.$Khi đó $g’\left( x \right)>0\Leftrightarrow f’\left( 3x \right)>{{\left( 3x \right)}^{2}}\Leftrightarrow 0<x<\frac{2}{3}$.
$\Rightarrow g’\left( x \right)<0$ trên $\left( -\infty ;0 \right);\left( \frac{2}{3};+\infty \right)$.
Ta có $g\left( 0 \right)=f\left( 0 \right)-{{9.0}^{3}}-1=0$.
Bảng biến thiên của hàm số $y=g\left( x \right)$.
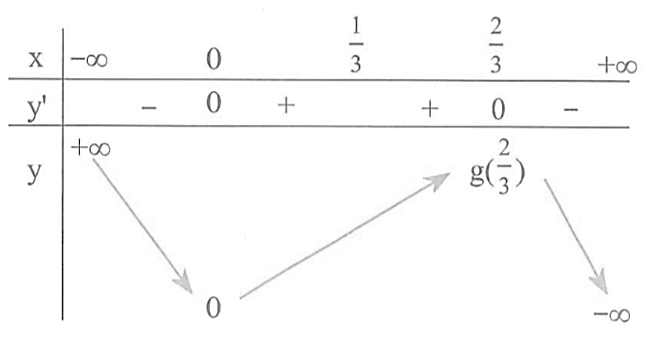
Từ bảng biến thiên ta có hàm số $y=\left| g\left( x \right) \right|$ đồng biến trên $\left( 0;\frac{2}{3} \right)$.




0 Bình luận