Đề 002-TN THPT QG

Đề 002-TN THPT QG

Câu 29. Cho hình chóp tứ giác $S.ABCD$ có $SA\bot \left( ABCD \right)$. ABCD là hình thang vuông tại A và B biết $AB=2a;AD=3BC=3a$. Tính thể tích khối chóp $S.ABCD$ theo a biết góc giữa mặt phẳng $\left( SCD \right)$ và $\left( ABCD \right)$ bằng $60{}^\circ $.

A. $2\sqrt{6}{{a}^{3}}$

B. $6\sqrt{6}{{a}^{3}}$

C. $2\sqrt{3}{{a}^{3}}$

D. $6\sqrt{3}{{a}^{3}}$.

Hướng dẫn và lời giải

Đáp án A

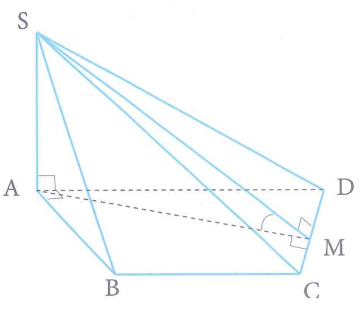
Dựng $AM\bot CD$ tại M. Ta có: $\widehat{SMA}=60{}^\circ $.

${{S}_{ABCD}}=\frac{AD+BC}{2}.AB=4{{a}^{2}}$.

$CD=\sqrt{{{\left( AD-BC \right)}^{2}}+A{{B}^{2}}}=2a\sqrt{2}$

${{S}_{ABC}}=\frac{1}{2}AB.BC={{a}^{2}}$.

${{S}_{ACD}}={{S}_{ABCD}}-{{S}_{ABC}}=3{{a}^{2}}.{{S}_{ACD}}=\frac{1}{2}AM.CD\Rightarrow AM=\frac{2{{S}_{ACD}}}{CD}=\frac{3\sqrt{2}}{2}a$

Ta có: $SA=AM.\tan \widehat{SMA}=\frac{3\sqrt{6}}{2}a\Rightarrow {{v}_{S.ABCD}}=\frac{1}{3}SA.{{S}_{ABCD}}=2\sqrt{6}{{a}^{3}}$.

Trở lại đề thi