Đề 002-TN THPT QG
Câu 34. Cho hình thang ABCD vuông tại A và D, $AB=AD=a,CD=2a$. Tính thể tích khối tròn xoay được tạo ra khi cho hình thang ABCD quay quanh trục AD.
A. $\frac{7\pi {{a}^{3}}}{3}$.
B. $\frac{4\pi {{a}^{3}}}{3}$.
C. $\frac{\pi {{a}^{3}}}{3}$.
D. $\frac{8\pi {{a}^{3}}}{3}$.
Hướng dẫn và lời giải
Đáp án A
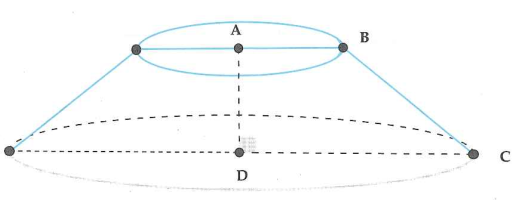
Khi cho hình thang ABCD quay quanh trục AD ta thu được khối nón cụt có đường cao AD, bán kính của đáy lớn là DC, bán kính đáy nhỏ là AB.
Áp dụng công thức tích thể tích khối nón cụt, ta có thể tích của khối tròn xoay tạo thành là:
$V=\frac{1}{3}h.\pi \left( {{R}_{1}}^{2}+{{R}_{2}}^{2}+{{R}_{1}}.{{R}_{2}} \right)$
$=\frac{1}{3}AD.\pi \left( A{{B}^{2}}+D{{C}^{2}}+AB.DC \right)=\frac{1}{3}a.\pi \left( {{a}^{2}}+4{{a}^{2}}+a.2a \right)=\frac{7\pi {{a}^{3}}}{3}$.
Vậy thể tích khối tròn xoay là $=\frac{7\pi {{a}^{3}}}{3}$.




0 Bình luận