Đề 002-TN THPT QG

Đề 002-TN THPT QG

Câu 36. Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên.

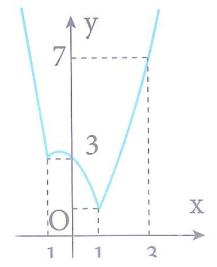
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $g\left( x \right)=f\left[ 2\left( {{\sin }^{4}}x+{{\cos }^{4}}x \right) \right]$. Tổng $M+m$ bằng

A. 3.                                 

B. 4.                                 

C. 5.                                 

D. 6.

Hướng dẫn và lời giải

Đáp án B

Vì ${{\sin }^{4}}x+{{\cos }^{4}}x=1-\frac{1}{2}{{\sin }^{2}}2x\in \left[ 1;2 \right].f\left( x \right)<\frac{3}{4},\forall x\in \left( 1;2 \right)$ Dựa vào đồ thị suy ra

$\left{ \begin{array}{l}
M = \max g\left( x \right) = f\left( 1 \right) = 3\
m = \min g\left( x \right) = f\left( 2 \right) = 1
\end{array} \right.$

Vậy $M+m=4$.

Trở lại đề thi