Đề 002-TN THPT QG

Đề 002-TN THPT QG

Câu 50. Cho tứ diện đều ABCD có cạnh bằng 3 cm. Gọi M là trung điểm của CD. Khoảng cách giữa AC và BM là

• A. $\frac{2\sqrt{11}}{11}cm$.

• B. $\frac{3\sqrt{22}}{11}cm$.

• C. $\frac{3\sqrt{2}}{11}cm$.

• D. $\frac{\sqrt{2}}{11}cm$.

Hướng dẫn và lời giải

Đáp án B

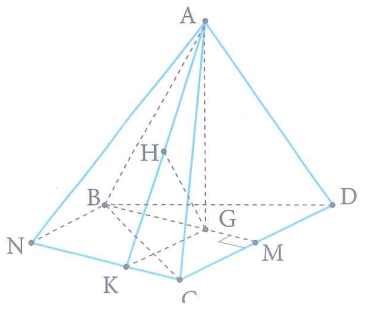
Gọi G là tâm tam giác đều BCD $\Rightarrow AG\bot \left( BCD \right)$.

Trong mặt phẳng $\left( BCD \right)$, dựng hình bình hành BMCN mà $BM\bot CM$ nên BMCN là hình chữ nhật.

Ta có $BM\text{//}\left( ACN \right)$

$\Rightarrow d\left( BM,AC \right)=d\left( BM,\left( ACN \right) \right)=d\left( G,\left( ACN \right) \right)$.

Kẻ $GK\bot NC\,\,\left( K\in NC \right)$ và $GH\bot AK\,\,\left( H\in AK \right)$

$\Rightarrow d\left( G,\left( ACN \right) \right)=GH$.

Ta có $AG=\sqrt{A{{B}^{2}}-B{{G}^{2}}}=\sqrt{9-{{\left( \frac{2}{3}.\frac{3\sqrt{3}}{2} \right)}^{2}}}=\sqrt{6}\,\,cm\,\,\,,GK=CM=\frac{3}{2}\,\,cm$. Vậy $GH=\frac{AG.GK}{\sqrt{A{{G}^{2}}+G{{K}^{2}}}}=\frac{\sqrt{6}.\frac{3}{2}}{\sqrt{6+\frac{9}{4}}}=\frac{3\sqrt{22}}{11}\,\,cm$.

Trở về đề thi