Đề 003-TN THPT QG

Đề 003-TN THPT QG

Câu 32.   Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB=a;AC=a\sqrt{3}$. Gọi $H$ là trung điểm $BC$ biết $SH$ vuông góc mặt phẳng $\left( ABC \right)$ và $SA$ tạo với đáy một góc ${{60}^{0}}$. Một hình nón có đỉnh $S$ và đáy là đường tròn ngoại tiếp tam giác $ABC$. Tính diện tích xung quanh của mặt nón đã cho.

A. $\frac{2\sqrt{3}\pi {{a}^{2}}}{3}$.                   

B. $4\pi {{a}^{2}}$.      

C. $2\sqrt{3}\pi {{a}^{2}}$.                                       

D. $2\pi {{a}^{2}}$.

Hướng dẫn và Lời giải

Chọn D

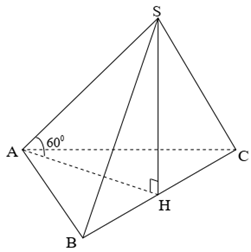
$BC=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a$;

$AH=\frac{1}{2}BC=a$

$\widehat{\left( SA,\left( ABC \right) \right)}=\widehat{SAH}={{60}^{0}}$

$SA=\frac{AH}{\cos {{60}^{0}}}=2a$

Mặt nón đã cho có $r=a;l=2a$

Nên ${{S}_{xp}}=\pi rl=2\pi {{a}^{2}}$.

Trở lại đề thi