Đề 003-TN THPT QG
Câu 46. Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau
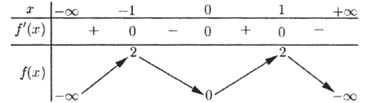
Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu diễn tập nghiệm của phương trình$f\left( f\left( \cos x \right) \right)=2$?
A. $2$.
B. $3$.
C. $6$.
D. $4$.
Hướng dẫn và Lời giải
Chọn D
Dựa vào bảng biến thiên ta có:
$f\left( {f\left( {\cos x} \right)} \right) = 2 \Leftrightarrow \left[ \begin{array}{l} f\left( {\cos x} \right) = – 1\\ f\left( {\cos x} \right) = 1 \end{array} \right.$ $+ f\left( {\cos x} \right) = – 1 \Leftrightarrow \left[ \begin{array}{l} \cos x = {t_1}\left( 1 \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \left( {{t_1} < - 1} \right)\\ \cos x = {t_2}\left( 2 \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \left( {{t_2} > 1} \right) \end{array} \right.$Dễ thấy phương trình $\left( 1 \right)$ và $\left( 2 \right)$ đều vô nghiệm.
$+ f\left( {\cos x} \right) = 1 \Leftrightarrow \left[ \begin{array}{l} \cos x = {t_3}\left( 3 \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \left( {{t_3} < - 1} \right)\\ \cos x = {t_4}\left( 4 \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \left( { - 1 < {t_4} < 0} \right)\\ \cos x = {t_5}\left( 5 \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \left( {0 < {t_5} < 1} \right)\\ \cos x = {t_6}\left( 6 \right){\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} \left( {{t_6} > 1} \right) \end{array} \right.$Ta thấy phương trình $\left( 3 \right)$ và $\left( 6 \right)$ đều vô nghiệm còn phương trình $\left( 4 \right)$ và $\left( 5 \right)$ mỗi phương trình tập nghiệm của nó đều được biểu diễn bởi hai điểm trên đường tròn lượng giác.
Vậy tập nghiệm của phương trình$f\left( f\left( \cos x \right) \right)=2$ được biểu diễn bởi bốn điểm trên đường tròn lượng giác.




0 Bình luận