Đề 004-TN THPT QG

Đề 004-TN THPT QG

Câu 40. Cho hình chóp $S.ABC$có đáy $ABC$là tam giác vuông cân, $AB=BC=2a.$ Tam giác $SAC$cân tại $S$và nằm trong mặt phẳng vuông góc với mặt phẳng $(ABC)$, $SA=a\sqrt{3}.$ Góc giữa hai mặt phẳng $(SAB)$ và $(SAC)$ bằng

A. ${{60}^{0}}$.            

B. ${{30}^{0}}$.          

C. ${{45}^{0}}$.          

D. ${{90}^{0}}.$

Hướng dẫn và Lời giải

Chọn đáp án A

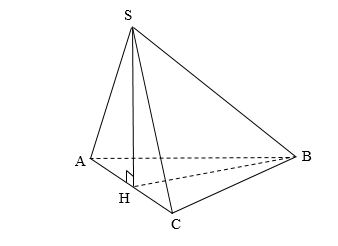
+ Gọi H là trung điểm của $AC$.

+ Do tam giác $ABC$ là tam giác vuông cân tại B nên $BH\bot AC\,\,\,\,\,(1).$

+ Do tam giác $SAC$cân tại $S$và nằm trong mặt phẳng vuông góc với mặt phẳng $(ABC)$ nên $SH\bot (ABC)\Rightarrow SH\bot BH\,\,\,\,(2).$

+ Từ (1) và (2) suy ra $BH\bot (SAC)$ hay hình chiếu của B trên $(SAC)$ là H, tức là hình chiếu của tam giác SAB trên $(SAC)$ là tam giác SAH.

+ Theo công thức diện tích hình chiếu ta có: ${{S}_{\Delta SAH}}={{S}_{\Delta SAB}}.\cos \varphi $, trong đó $\varphi $  là góc giữa hai mặt phẳng $(SAB)$ và $(SAC)$.

+ Xét tam giác$ABC$ vuông cân, $AB=BC=2a$$\Rightarrow AC=\sqrt{2}AB=2a\sqrt{2}\Rightarrow AH=\frac{AC}{2}=a\sqrt{2}.$

+ Xét tam giác SAH vuông tại H, có $SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=a.$

Suy ra ${{S}_{\Delta SAH}}=\frac{1}{2}SH.AH=\frac{{{a}^{2}}\sqrt{2}}{2}.$

+ Xét tam giác ABC vuông tại B suy ra $BH=\frac{AC}{2}=a\sqrt{2}.$

+ Xét tam giác SBH vuông tại H, có $SB=\sqrt{S{{H}^{2}}+B{{H}^{2}}}=a\sqrt{3}.$

Suy ra tam giác SAB cân tại S. Gọi I là trung điểm của AB thì $SI\bot AB$và $SI=\sqrt{S{{A}^{2}}-{{\left( \frac{AB}{2} \right)}^{2}}}=a\sqrt{2}.$

Nên ${{S}_{\Delta SAB}}=\frac{1}{2}SI.AB={{a}^{2}}\sqrt{2}\Rightarrow \cos \varphi =\frac{{{S}_{\Delta SAH}}}{{{S}_{\Delta SAB}}}=\frac{1}{2}\Rightarrow \varphi ={{60}^{0}}.$

Trở lại đề thi