Đề 004-TN THPT QG

Đề 004-TN THPT QG

Câu 43. [Mức độ 3] Có bao nhiêu số nguyên a để phương trình ${{6}^{x}}-{{2}^{x}}-{{3}^{x}}=\frac{a}{5}$ có hai nghiệm thực phân biệt?

A. $1$.                           

B. $5$.                         

C. $4$.                         

D. Vô số.

Hướng dẫn và Lời giải

Chọn đáp án C

Xét hàm số $f\left( x \right)={{6}^{x}}-{{2}^{x}}-{{3}^{x}},\,\forall x\in \mathbb{R}$.

Ta có ${f}’\left( x \right)=0\Leftrightarrow {{6}^{x}}\ln 6-{{2}^{x}}\ln 2-{{3}^{x}}\ln 3\Leftrightarrow {{6}^{x}}\ln 6={{2}^{x}}\ln 2+{{3}^{x}}\ln 3\Leftrightarrow x=0$

BBT hàm số $f\left( x \right)$

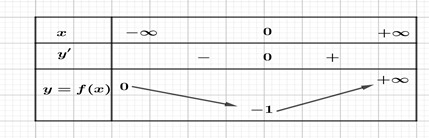
Vậy phương trình đã cho có 2 nghiệm thực khi và chỉ khi $-1<\frac{a}{5}<0\Leftrightarrow -5<a<0$.

Vì $a\in \mathbb{Z}$ nên $a=\left\{ -4\,;\,-3\,;\,-2\,;\,-1\, \right\}$. Suy ra có 4 giá trị a thỏa mãn yêu cầu bài toán.

Trở lại đề thi