Đề 004-TN THPT QG
Câu 48. [Mức độ 4] Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Mặt bên $SAB$ là tam giác đều cạnh $\sqrt{3}a$, $ABC$ là tam giác vuông tại $A$ có cạnh $AC=a$, góc giữa $AD$ và $(SAB)$ bằng $30{}^\circ $. Thể tích khối chóp $S.ABCD$ bằng
A. ${{a}^{3}}$.
B. $\frac{\sqrt{3}{{a}^{3}}}{6}$.
C. $\frac{\sqrt{3}{{a}^{3}}}{2}$.
D. $\frac{\sqrt{3}{{a}^{3}}}{4}$
Hướng dẫn và Lời giải
Chọn đáp án C
Cách 1:
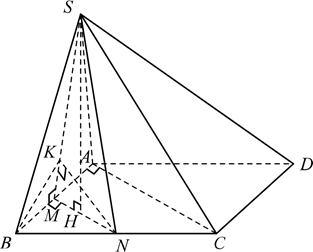
Ta có: $BC=AD=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=2a;SM=\frac{AB\sqrt{3}}{2}=\frac{3a}{2}$.
Gọi $M,N$ lần lượt là trung điểm $AB,BC$.
$\Rightarrow MN\text{//}AC\Rightarrow MN\bot AB$.
Do tam giác $SAB$ đều nên $SM\bot AB$
$\begin{array}{l} \Rightarrow AB \bot (SMN)\\ \Rightarrow \left\{ \begin{array}{l} (SMN) \bot (ABCD)\\ (SMN) \bot (SAB) \end{array} \right. \end{array}$Kẻ $SH\bot MN\Rightarrow SH\bot (ABC)$ do $(SMN)\bot (ABCD)$.
Kẻ $NK\bot SM\Rightarrow NK\bot (SAB)$ do $(SMN)\bot (SAB)$.
Do $BN\text{//}AD$ góc giữa $AD$ và $(SAB)$ bằng góc giữa $BN$ và $(SAB)$.
Do $NK\bot (SAB)$ nên góc giữa $BN$ và $(SAB)$ là góc $\widehat{NBK}=30{}^\circ $.
Xét tam giác vuông $NBK$ ta có: $\sin \widehat{NBK}=\frac{NK}{BN}\Leftrightarrow \frac{1}{2}=\frac{NK}{a}\Leftrightarrow NK=\frac{a}{2}$.
Mặt khác: $NK.SM=SH.MN\Leftrightarrow \frac{a}{2}.\frac{3a}{2}=SH.\frac{a}{2}\Leftrightarrow SH=\frac{3a}{2}$.
Vậy ${{V}_{SABCD}}=\frac{1}{3}.{{S}_{ABCD}}.SH=\frac{1}{3}.2{{S}_{ABC}}.SH=\frac{2}{3}.\frac{1}{2}AB.AC.SH=\frac{{{a}^{3}}\sqrt{3}}{2}$.
Cách 2:
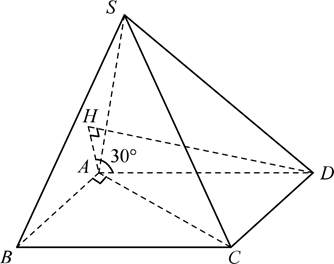
Gọi $D$ là hình chiếu vuông góc của $D$ trên $(SAB)$.
$\Rightarrow $Góc giữa $AD$ và $(SAB)$ là góc $\widehat{DAH}=30{}^\circ $.
Ta có: $AD=BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=2a$.
$\Rightarrow \sin \widehat{DAH}=\frac{DH}{DA}\Leftrightarrow \sin 30{}^\circ =\frac{DH}{2a}\Leftrightarrow DH=a$.
Ta có: ${{V}_{DSAB}}=\frac{1}{3}{{S}_{SAB}}.DH=\frac{1}{3}.\frac{{{\left( a\sqrt{3} \right)}^{2}}\sqrt{3}}{4}.a=\frac{{{a}^{3}}\sqrt{3}}{4}$.
Mặt khác do $ABCD$ là hình bình hành nên ${{V}_{SABCD}}=2{{V}_{SABD}}=2{{V}_{DSAB}}=\frac{{{a}^{3}}\sqrt{3}}{2}$.



0 Bình luận