Đề 004-TN THPT QG
Câu 50. [Mức độ 4] Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{{x}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z+3 \right)}^{2}}=24$ cắt mặt phẳng $\left( \alpha \right):x+y=0$ theo giao tuyến là đường tròn $\left( C \right)$. Tìm hoành độ của điểm $M$ thuộc đường tròn $\left( C \right)$ sao cho khoảng cách từ $M$ đến $A\left( 6;-10;3 \right)$ lớn nhất.
A. $-1$.
B. $-4$.
C. $2$.
D. $-5$.
Hướng dẫn và Lời giải
Chọn đáp án B
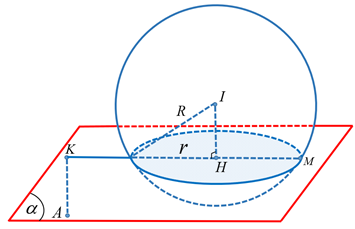
Mặt cầu có tâm $I\left( 0;2;-3 \right)$, bán kính$R=2\sqrt{6}$.
Gọi $H$ là tâm đường tròn giao tuyến.
Khi đó $H\left( t;2+t;-3 \right)\in \left( \alpha \right)\Leftrightarrow t=-1\Rightarrow H\left( -1;1;-3 \right)$.
Ta có $IH=\sqrt{2}\Rightarrow r=\sqrt{22}$.
Gọi $K$ là hình chiếu của $A$ lên $\left( \alpha \right)$.
Khi đó $K\left( 6+a;-10+a;3 \right)\in \left( \alpha \right)\Leftrightarrow a=2\Rightarrow K\left( 8;-8;3 \right)$.
Ta có $HK=3\sqrt{22}>r$.
$A{{M}^{2}}=\left( A{{K}^{2}}+K{{M}^{2}} \right)\max \Leftrightarrow KM\max \Leftrightarrow \overrightarrow{KH}=3\,\,\overrightarrow{HM}$
$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} 3\left( {x + 1} \right) = – 9\\ 3\left( {y – 1} \right) = 9\\ 3\left( {z + 3} \right) = – 6 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = – 4\\ y = 4\\ z = – 5 \end{array} \right.\\ \Leftrightarrow M\left( { – 4;4; – 5} \right) \end{array}$


0 Bình luận