Hai mặt phẳng song song
I.Định nghĩa.
1.1. Vị trí tương đối của hai mặt phẳng phân biệt
Cho 2 mp phân biệt (P), (Q).
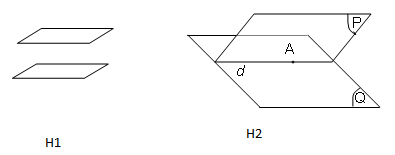
- $\left( P \right) \cap \left( Q \right){\rm{ }} = {\rm{ }}a$ $ \Leftrightarrow $ $\left( P \right)$ cắt $\left( Q \right)$.
- $\left( P \right) \cap \left( Q \right){\rm{ }} = \phi \Leftrightarrow \left( P \right){\rm{ }}//{\rm{ }}\left( Q \right)$
1.2. Định nghĩa
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung, kí hiệu $\left( \alpha \right)\parallel \left( \beta \right)$.
Vậy $\left( \alpha \right)\parallel \left( \beta \right)\Leftrightarrow \left( \alpha \right)\cap \left( \beta \right)=\varnothing $.
2. Định lý và tính chất.
2.1. Định lý 1.
| Nếu mặt phẳng $\left( \alpha \right)$ chứa hai đường thẳng cắt nhau $a,b$ và hai đường thẳng này cùng song song với mặt phẳng $\left( \beta \right)$ thì $\left( \alpha \right)\parallel \left( \beta \right)$. |
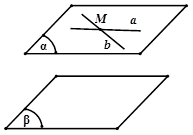
Vậy
$\left\{ \begin{array}{l}
a \subset \left( \alpha \right),b \subset \left( \alpha \right)\\
a \cap b = M\\
a\parallel \left( \beta \right),b\parallel \left( \beta \right)
\end{array} \right. \Rightarrow \left( \alpha \right)\parallel \left( \beta \right).$
2.2. Định lý 2.
Qua một điểm nằm ngoài mặt phẳng có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Hệ quả 1
Nếu $d\parallel \left( \alpha \right)$ thì trong $\left( \alpha \right)$ có một đường thẳng song song với $d$ và qua $d$ có duy nhất một mặt phẳng song song với $\left( \alpha \right)$.
Hệ quả 2
Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song.
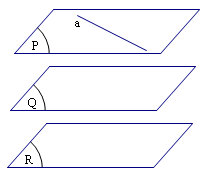
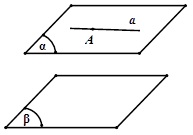
Hệ quả 3
Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$. Mọi đường thẳng đi qua $A$ và song song với $\left( \alpha \right)$ đều nằm trong mặt phẳng qua $A$ song song với $\left( \alpha \right)$.
Vậy
$\left\{ \begin{array}{l}
A \notin \left( \alpha \right),A \in \left( \beta \right)\\
A \in d\\
d\parallel \left( \alpha \right)\\
\left( \beta \right)\parallel \left( \alpha \right)
\end{array} \right. \Rightarrow d \subset \left( \beta \right).$
2.3. Định lý 3
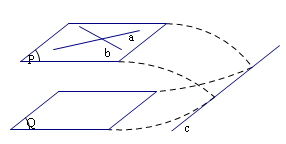
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến đó song song với nhau.
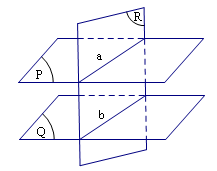
Vậy
$\left\{ \begin{array}{l}
\left( \alpha \right)\parallel \left( \beta \right)\\
\left( \delta \right) \cap \left( \alpha \right) = a
\end{array} \right. \Rightarrow \left( \delta \right) \cap \left( \beta \right) = b\parallel a.$
Hệ quả
Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn bằng nhau.
2.4. Định lí Ta-lét (Thales)
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
$\left\{ \begin{array}{l}
\left( \alpha \right)\parallel \left( \beta \right)\parallel \left( \chi \right)\\
{d_1} \cap \left( \alpha \right) = {A_1},{d_1} \cap \left( \beta \right) = {B_1},{d_1} \cap \left( \chi \right) = {C_1}\\
{d_2} \cap \left( \alpha \right) = {A_2},{d_2} \cap \left( \beta \right) = {B_2},{d_2} \cap \left( \chi \right) = {C_2}
\end{array} \right.$
$ \Rightarrow \frac{{{A_1}{B_1}}}{{{B_1}{C_1}}} = \frac{{{A_2}{B_2}}}{{{B_2}{C_2}}}.$
2.5. Định lí Ta-lét( Thales) đảo
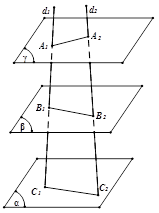
Cho hai đường thẳng ${{d}_{1}},{{d}_{2}}$ chéo nhau và các điểm ${{A}_{1}},{{B}_{1}},{{C}_{1}}$ trên ${{d}_{1}}$, các điểm ${{A}_{2}},{{B}_{2}},{{C}_{2}}$ trên ${{d}_{2}}$ sao cho $\frac{{{A}_{1}}{{B}_{1}}}{{{B}_{1}}{{C}_{1}}}=\frac{{{A}_{2}}{{B}_{2}}}{{{B}_{2}}{{C}_{2}}}$. Lúc đó các đường thẳng ${{A}_{1}}{{A}_{2}},{{B}_{1}}{{B}_{2}},{{C}_{1}}{{C}_{2}}$ cùng song song với một mặt phẳng.
2.6. Định lý Menelaus
2.6.1. Định lý
Gọi $M,N,P,Q$ theo thứ tự là các điểm trên các đường thẳng $AB,BC,CD,DA$ của tứ diện $ABCD$( $M,N,P,Q$ khác với $A,B,C,D$) thì $M,N,P,Q$ đồng phẳng khi và chỉ khi $\frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PD}.\frac{QD}{QA}=1$.
2.6.2. Chứng minh định lý Menelaus.
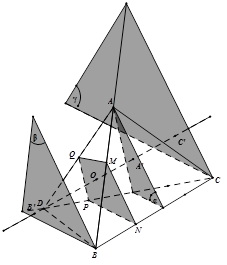
Phần thuận.
Giả sử $M,N,P,Q$ đồng phẳng. Từ các đỉnh $A,B,C$ dựng các mặt phẳng $\left( \alpha \right),\left( \beta \right),\left( \gamma \right)$ theo thứ tự song song với $\left( MNPQ \right)$.
Từ $D$ dựng đường thẳng $d$ cắt $\left( \alpha \right),\left( \beta \right),\left( \gamma \right)$ theo thứ tự tại $A’,B’,C’$ và cắt $\left( MNPQ \right)$ tại $O$.
Ta có $\frac{OA’}{OB’}.\frac{OB’}{OC’}.\frac{OC’}{OD}.\frac{OD}{OA’}=1$
Theo định lí Thales thì $\frac{OA’}{OB’}=\frac{MA}{MB}$ $\frac{OB’}{OC’}=\frac{NB}{NC},\frac{OC’}{OD}=\frac{PC}{PD},\frac{OD}{OA’}=\frac{QD}{QA}$$\frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PD}.\frac{QD}{QA}=$$\frac{OA’}{OB’}.\frac{OB’}{OC’}.\frac{OC’}{OD}.\frac{OD}{OA’}=1$.
Phần đảo.
Giả sử $\frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PD}.\frac{QD}{QA}=1$. Gọi $E=\left( MNP \right)\cap AD$ theo chứng minh trên,do $M,N,P,E$ đồng phẳng nên $\frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PD}.\frac{ED}{EA}=1$$\Rightarrow \frac{QD}{QA}=\frac{ED}{EA}\Rightarrow E\equiv Q$.
Vậy $M,N,P,Q$ đồng phẳng.
3. Hình lăng trụ và hình chóp cụt.
3.1. Hình lăng trụ
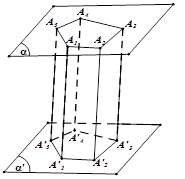
| Cho hai mặt phẳng song song $\left( \alpha \right)$ và $\left( \alpha ‘ \right)$. Trên $\left( \alpha \right)$ cho đa giác ${{A}_{1}}{{A}_{2}}…{{A}_{n}}$. Qua các đỉnh ${{A}_{1}},{{A}_{2}},…,{{A}_{n}}$ vẽ các đường thẳng song song với nhau cắt $\left( \alpha ‘ \right)$ lần lượt tại $A_{1}^{‘},A_{2}^{‘},…,A_{n}^{‘}$. Hình gồm hai đa giác ${{A}_{1}}{{A}_{2}}…{{A}_{n}}$ , $A_{1}^{‘}A_{2}^{‘}…A_{n}^{‘}$ và các hình bình hành ${{A}_{1}}A_{1}^{‘}A_{2}^{‘}{{A}_{2}},{{A}_{2}}A_{2}^{‘}A_{3}^{‘}{{A}_{3}},…,{{A}_{n}}A_{n}^{‘}A_{1}^{‘}{{A}_{1}}$ được gọi là hình lăng trụ ${{A}_{1}}{{A}_{2}}…{{A}_{n}}.A_{1}^{‘}A_{2}^{‘}…A_{n}^{‘}$. Lăng trụ có đáy là hình bình hành được gọi là hình hộp. |
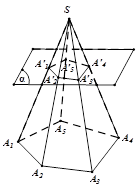
3.2. Hình chóp cụt.
| Cho hình chóp $S.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$. Một mặt phẳng không đi qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh bên $S{{A}_{1}},S{{A}_{2}},..,S{{A}_{n}}$ lần lượt tại $A_{1}^{‘},A_{2}^{‘},..A_{n}^{‘}$. Hình tạo bởi thiết diện $A_{1}^{‘}A_{2}^{‘}…A_{n}^{‘}$ và đáy ${{A}_{1}}{{A}_{2}}…{{A}_{n}}$ cùng với các tứ giác $A_{1}^{‘}A_{2}^{‘}{{A}_{2}}{{A}_{1}},A_{2}^{‘}A_{3}^{‘}{{A}_{3}}{{A}_{2}},…,A_{n}^{‘}A_{1}^{‘}{{A}_{1}}{{A}_{n}}$ gọi là hình chóp cụt $A_{1}^{‘}A_{2}^{‘}…A_{n}^{‘}.{{A}_{1}}{{A}_{2}}…{{A}_{n}}$. | . |
—————-
Xem thêm:
0 Bình luận