Hàm số lũy thừa
I. Định nghĩa và tính chất
• Định nghĩa: Hàm số \(y=f\left(x\right)=x^a\) được gọi là hàm số lũy thừa.
- Tập xác định:
+ 
nếu α là số nguyên dương.
+ 
nếu α nguyên âm hoặc bằng 0.
+ D=(0;+∞) với α không nguyên.
• Đạo hàm : \(y’=a.x^{a-1}\).
+ Đạo hàm hàm hợp \(y=u^{\alpha}\) thì \(y=\alpha.u’.u^{\alpha-1}\))
• – Tính chất của hàm số lũy thừa trên khoảng (0;+∞):
+ a > 0 : Hàm số luôn đồng biến.
+ a < 0 : Hàm số luôn nghịch biến
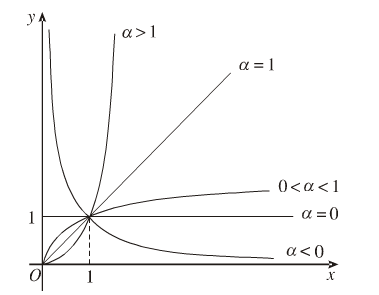
II. Hàm số lũy thừa
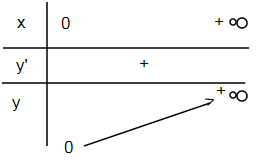
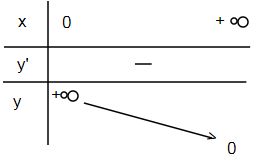
Xét 2 trường hợp: \(\alpha>0\) và \(\alpha< 0\).
| \(y=x^{\alpha}\) (\(\alpha>0\)) | \(y=x^{\alpha}\) (\(\alpha< 0\)) | |
| Miền khảo sát | \(\left(0;+\infty\right)\)
Chú ý: khi khảo sát với \(\alpha\) cụ thể, miền xác định có thể là R) |
\(\left(0;+\infty\right)\)
Chú ý: khi khảo sát với \(\alpha\) cụ thể, miền xác định có thể là R) |
| Sự biến thiên | \(y’=\alpha x^{\alpha-1}>0,\forall x>0\)
Giới hạn đặc biệt: $\lim\limits_{x\rightarrow+0}x^{\alpha}=0$; $\lim\limits_{x\rightarrow+\infty}x^{\alpha}=+\infty$ Tiệm cận: không có |
\(y’=\alpha x^{\alpha-1}>0,\forall x>0\)
Giới hạn đặc biệt: $\lim\limits_{x\rightarrow0^+}x^{\alpha}=+\infty$; $\mathop {\lim }\limits_{x \to + \infty } {x^\alpha } = 0$ Tiệm cận: -TCN: trục Ox – TCĐ: trục Oy |
| Bảng biến thiên |  |
 |
| Đồ thị | 
Đồ thị luôn đi qua (1;1) |
|
III. Dạng bài tập cơ bản
Dạng 1. Tìm tập xác định của hàm số
A. Phương pháp
* Hàm số lũy thừa ![y={{\text{ }\!\![\!\!\text{ }u(x)\text{ }\!\!]\!\!\text{ }}^{\alpha }}](http://s0.wp.com/latex.php?latex=y%3D%7B%7B%5Ctext%7B+%7D%5C%21%5C%21%5B%5C%21%5C%21%5Ctext%7B+%7Du%28x%29%5Ctext%7B+%7D%5C%21%5C%21%5D%5C%21%5C%21%5Ctext%7B+%7D%7D%5E%7B%5Calpha+%7D%7D&bg=ffffff&fg=000&s=0 "y={{\text{ }\!\![\!\!\text{ }u(x)\text{ }\!\!]\!\!\text{ }}^{\alpha }}")
:
+ Xác định với mọi 
nếu 
nguyên dương.
+ Xác định với 
nếu nguyên âm.
+ Xác định với 
nếu không nguyên.
B. Ví dụ
Ví dụ 1: Tập xác định của hàm số 
là
A. ![\displaystyle \text{ }\!\![\!\!\text{ }-1;-\frac{1}{2}\text{ }\!\!]\!\!\text{ }\cup \text{ }\!\![\!\!\text{ }0;\frac{4}{3}\text{ }\!\!]\!\!\text{ }](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Ctext%7B+%7D%5C%21%5C%21%5B%5C%21%5C%21%5Ctext%7B+%7D-1%3B-%5Cfrac%7B1%7D%7B2%7D%5Ctext%7B+%7D%5C%21%5C%21%5D%5C%21%5C%21%5Ctext%7B+%7D%5Ccup+%5Ctext%7B+%7D%5C%21%5C%21%5B%5C%21%5C%21%5Ctext%7B+%7D0%3B%5Cfrac%7B4%7D%7B3%7D%5Ctext%7B+%7D%5C%21%5C%21%5D%5C%21%5C%21%5Ctext%7B+%7D&bg=ffffff&fg=000&s=0 "\displaystyle \text{ }\!\![\!\!\text{ }-1;-\frac{1}{2}\text{ }\!\!]\!\!\text{ }\cup \text{ }\!\![\!\!\text{ }0;\frac{4}{3}\text{ }\!\!]\!\!\text{ }")
. B. 
.
C. 
. D. 
.
Lời giải:
Hàm số xác định 
.
Chọn C.
Ví dụ 2: Tập xác định của hàm số 
là
A. 
. B. 
.
C. 
. D. 
.
Lời giải:
Hàm số đã cho xác định
Vậy tập xác định của hàm số là 
.
Chọn C.
Dạng 2. Tính đạo hàm
A. Phương pháp
– Bảng đạo hàm của các hàm số sơ cấp thường gặp:
B. Bài tập ví dụ
Ví dụ 3: Cho hàm số sau : $y = {\left( {{x^2} – 2x – 3} \right)^{ – 2}}$. Giải phương trình y’=0
Lời giải
Vì lũy thừa bằng -2 thuộc số nguyên, ta có:
ĐK: ${x^2} – 2x – 3 \ne 0 \Leftrightarrow x = – 1;x = 3$
=>TXĐ: $D = R\backslash \left\{ { – 1;3} \right\}$
$y’ = – 2.{\left( {{x^2} – 2x – 3} \right)^{ – 3}}({x^2} – 2x – 3)’$ $ = – 2.{\left( {{x^2} – 2x – 3} \right)^{ – 3}}(2x – 2)$;$\forall x > 3$.
$y’ = 0 \Leftrightarrow – 2.{\left( {{x^2} – 2x – 3} \right)^{ – 3}}(2x – 2) = 0 \Leftrightarrow x = 1$. Vậy phương trình y’=0 có nghiệm x=1.
Dạng 3. Đồ thị của hàm số lũy thừa
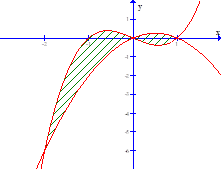
Ví dụ 4: Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
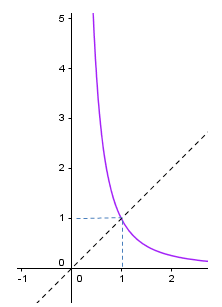
A. $y = {x^3}$. B. $y = {x^{ – 1}}$. C. $y = {x^2}$. D. $y = {x^{ – \frac{2}{3}}}$.
Lời giải:
Nhận thấy đồ thị của hàm số nằm bên phải 0y=>x>0.
Hàm số luôn nghịch biến nên α<0. Chọn D.
0 Bình luận