Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai-Kỹ thuật đặt ẩn phụ đưa về hệ đối xứng loại 2

Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai

Kỹ thuật đặt ẩn phụ đưa về hệ đối xứng loại 2

Phương pháp

Dạng : ${{\left( \alpha x+\beta \right)}^{n}}=p\sqrt[n]{a’x+b’}+\gamma $ đặt $\alpha y+\beta =\sqrt[n]{ax+b}$ để đưa về hệ đối xứng loại 2.

$(*)\left\{ \begin{array}{l}
{\left( {\alpha x + \beta } \right)^n} = ay + b\\
{\left( {\alpha y + \beta } \right)^n} = ax + b
\end{array} \right.$

Ví dụ minh họa

Ví dụ 1.

Giải phương trình: ${{x}^{2}}-2x=2\sqrt{2x-1}$

Giải

Điều kiện: $x\ge \frac{1}{2}$

Ta có phương trình được viết lại là: ${{(x-1)}^{2}}-1=2\sqrt{2x-1}$.

Đặt $y-1=\sqrt{2x-1}$ thì ta đưa về hệ sau:

$\left\{ \begin{array}{l}
{x^2} – 2x = 2(y – 1)\\
{y^2} – 2y = 2(x – 1)
\end{array} \right.$

Trừ hai vế của phương trình ta được $(x-y)(x+y)=0$

\[\begin{array}{l}
*)x = y\\
\Leftrightarrow \sqrt {2x – 1} = x – 1\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x – 1 \ge 0}\\
{2x – 1 = {{\left( {x – 1} \right)}^2}}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \ge 1}\\
{{x^2} – 4x + 2 = 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
\begin{array}{*{20}{c}}
{x \ge 1}\\
{x = 2 \pm \sqrt 2 }
\end{array}\\
\Leftrightarrow x = 2 + \sqrt 2
\end{array} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \ge 1}\\
{x = 2 \pm \sqrt 2 }
\end{array}} \right.\\
\Leftrightarrow x = 2 + \sqrt 2
\end{array}\]

\[\begin{array}{l}
*)x = – y\\
\Leftrightarrow \sqrt {2x – 1} = – x – 1\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{ – x – 1 \ge 0}\\
{2x – 1 = {{\left( { – x – 1} \right)}^2}}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \le – 1}\\
{{x^2} + 2 = 0}
\end{array}} \right.\\
\Leftrightarrow x = \phi
\end{array}\]

Giải ra ta tìm được nghiệm của phương trình là: $x=2+\sqrt{2}$

Ví dụ 2.

Giải phương trình: $2{{x}^{2}}-6x-1=\sqrt{4x+5}$

Giải

Điều kiện $x\ge -\frac{5}{4}$

Ta biến đổi phương trình như sau: $4{{x}^{2}}-12x-2=2\sqrt{4x+5}$$\Leftrightarrow {{(2x-3)}^{2}}=2\sqrt{4x+5}+11$

Đặt $2y-3=\sqrt{4x+5}$.

Ta được hệ phương trình sau:

$\left\{ \begin{array}{l}
{(2x – 3)^2} = 4y + 5\\
{(2y – 3)^2} = 4x + 5
\end{array} \right.$

$ \Rightarrow (x – y)(x + y – 1) = 0$

Với:$x=y\Rightarrow 2x-3=\sqrt{4x+5}$$\Rightarrow x=2+\sqrt{3}$.
Với: $x+y-1=0\Rightarrow y=1-x$$\Rightarrow x=1-\sqrt{2}$

Vậy phương trình có nghiệm: $x = 2 + \sqrt 3 $;$x = 1 – \sqrt 2 $

Ví dụ 3.

Giải phương trình: $\sqrt{2-x}=2-{{x}^{2}}$

Giải

Điều Kiện:$x\le 2$

Đặt $t=\sqrt{2-x};t\ge 0$$\Leftrightarrow {{t}^{2}}=2-x$$\Leftrightarrow 2={{t}^{2}}+x$

$\begin{array}{l}
\left( 1 \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{t = 2 – {x^2}}\\
{x = 2 – {t^2}}
\end{array}} \right.\\
\Leftrightarrow {t^2} – {x^2} + x – t = 0\\
\Leftrightarrow \left( {t – x} \right)\left( {t + x} \right) + x – t = 0\\
\Leftrightarrow \left( {t – x} \right)\left( {t + x – 1} \right) = 0\\
\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{t = x}\\
{t = 1 – x}
\end{array}} \right.
\end{array}$

$\begin{array}{l}
+ )t = x \Leftrightarrow \sqrt {2 – x} = x\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \ge 0}\\
{{x^2} + x – 2 = 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \ge 0}\\
{\left[ {\begin{array}{*{20}{c}}
{x = 1}\\
{x = – 2}
\end{array}} \right.}
\end{array}} \right.\\
\Leftrightarrow x = 1
\end{array}$

$\begin{array}{l}
+ )t = 1 – x \Leftrightarrow \sqrt {2 – x} = 1 – x\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \le 1}\\
{2 – x = {{\left( {1 – x} \right)}^2}}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \le 1}\\
{{x^2} – x – 1 = 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x \le 1}\\
{\left[ {\begin{array}{*{20}{c}}
{x = \frac{{1 + \sqrt 5 }}{2}}\\
{x = \frac{{1 – \sqrt 5 }}{2}}
\end{array}} \right.}
\end{array}} \right.\\
\Leftrightarrow x = \frac{{1 – \sqrt 5 }}{2}
\end{array}$

Vậy phương trình có nghiệm: $x = 1$; $x = \frac{{1 – \sqrt 5 }}{2}$

Bài tập thực hành

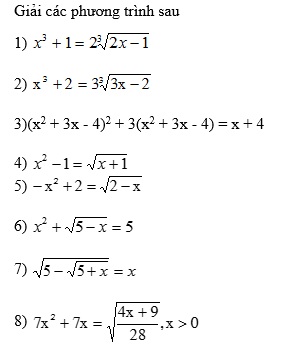
Sáng tạo

Ta hãy đi tìm nguồn gốc của những bài toán giải phương trình bằng cách đưa về hệ đối xứng loại II.

Ta xét một hệ phương trình đối xứng loại II sau :

$\left\{ \begin{array}{l}
{\left( {x + 1} \right)^2} = y + 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1)\\
{\left( {y + 1} \right)^2} = x + 2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (2)
\end{array} \right.$

Việc giải hệ trên ta xem lại chuyên mục giải hệ đối xưng loại II.

Bây giời ta sẽ biến hệ thành phương trình bằng cách đặt $y=f\left( x \right)$ sao cho (2) luôn đúng , $y=\sqrt{x+2}-1$, khi đó ta có phương trình :

${{\left( x+1 \right)}^{2}}=(\sqrt{x+2}-1)+1\Leftrightarrow {{x}^{2}}+2x=\sqrt{x+2}$

Vậy để giải phương trình : ${{x}^{2}}+2x=\sqrt{x+2}$ ta đặt lại như trên và đưa về hệ bằng cách tương tự xét hệ tổng quát dạng bậc 2 :

$\left\{ \begin{array}{l}
{\left( {\alpha x + \beta } \right)^2} = ay + b\\
{\left( {\alpha y + \beta } \right)^2} = ax + b
\end{array} \right.$

Tổng quát:

Xuất phát từ hệ tổng quát dạng bậc 2 (hệ gốc ):

$(*)\left\{ \begin{array}{l}
{\left( {\alpha x + \beta } \right)^2} = ay + b\\
{\left( {\alpha y + \beta } \right)^2} = ax + b
\end{array} \right.$

Ta sẽ xây dựng được phương trình dạng khai triển sau :

${{\left( \alpha x+\beta \right)}^{2}}=\frac{a}{\alpha }\sqrt{ax+b}+b-\frac{\beta }{\alpha }$ bằng cách đặt $\alpha y+\beta =\sqrt{ax+b}$.

Việc chọn $\alpha ;\beta $ thông thường chúng ta chỉ cần viết dưới dạng :${{\left( \alpha x+\beta \right)}^{n}}=p\sqrt[n]{a’x+b’}+\gamma $ là chọn được.
Việc giải phương trình khai triển ta làm ngược lại.
Tương tự cho bậc cao hơn : ${{\left( \alpha x+\beta \right)}^{n}}=\frac{a}{\alpha }\sqrt[n]{ax+b}+b-\frac{\beta }{\alpha }$

————————-

Download tài liệu:

PDF: tại đây.

Word: Tại đây.

————————–

Xem thêm:

———————-

User

Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai-Kỹ thuật đặt ẩn phụ đưa về hệ đối xứng loại 2

Đăng bởi ADMIN vào 17/12/201917/12/2019