I. Phương trình: sin x=m
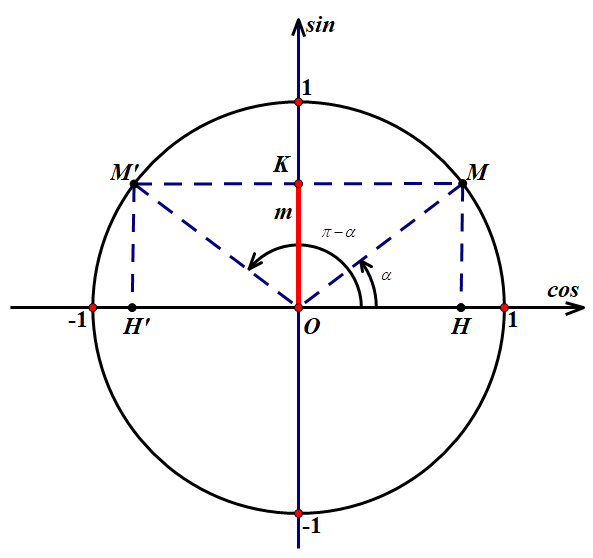
- Nếu \(|m|>1\): Không tồn tại giá trị nào của x sao cho sinx=m. Vậy phương trình vô nghiệm.
- Nếu \(|m|\leq 1\):
Tồn tại $\alpha $ sao cho:$\sin \alpha = m$. Suy ra $\alpha $ là một nghiệm.
Mặt khác: Do $\alpha $ là một nghiệm. Nên suy ra:
- $\sin \left( {\alpha + k2\pi } \right) = m$. Vậy ${\alpha + k2\pi }$ cũng là nghiệm.
- $\sin \left( {\pi – \alpha } \right) = m$. Vậy ${\pi – \alpha }$ cũng là nghiệm.
- $\sin \left( {\pi – \alpha + k2\pi } \right) = m$. Vậy ${\pi – \alpha + k2\pi }$ là nghiệm.
Tóm lại
\(\forall m,\left| m \right| \le 1, \sin x =m= \sin \alpha \Leftrightarrow \left[ \begin{array}{l} x = \alpha + k2\pi \\ x = \pi – \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Chú ý:
- \(\sin x =m= \sin {\beta ^0} \Leftrightarrow \left[ \begin{array}{l} x = {\beta ^0} + k{360^0}\\ x = {180^0} – {\beta ^0} + k{360^0} \end{array} \right.\left( {k \in\mathbb{Z} } \right)\)
- \(\sin x = m \Leftrightarrow \left[ \begin{array}{l} x = arc\sin (m) + k2\pi \\ x = \pi – arc\sin (m) + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Tổng quát:
\(\sin f\left( x \right) = \sin g\left( x \right) \Leftrightarrow \left[ \begin{array}{l} f\left( x \right) = g\left( x \right) + k2\pi \\ f\left( x \right) = \pi – g\left( x \right) + k2\pi \end{array} \right.\,\,\left( {k \in\mathbb{Z} } \right)\)
Các trường hợp đặc biệt:
\(\begin{array}{l} \oplus \,\,\,\sin x = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\\ \oplus \,\,\,\sin x = – 1 \Leftrightarrow x = – \frac{\pi }{2} + k2\pi \,\,\,\left( {k \in\mathbb{Z} } \right)\\ \oplus \,\,\,\sin x = 0 \Leftrightarrow x = k\pi \,\,\,\left( {k \in\mathbb{Z} } \right) \end{array}\)
Ví dụ :
Giải phương trình: $ \sin x = \frac{{\sqrt 3 }}{2}$.
Giải
$\sin x = \frac{{\sqrt 3 }}{2} = \sin \frac{\pi }{3}$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{3} + k2\pi }\\
{x = \pi – \frac{\pi }{3} + k2\pi }
\end{array}} \right.$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{3} + k2\pi }\\
{x = \frac{{2\pi }}{3} + k2\pi }
\end{array}} \right.\left( {k \in Z} \right)$
Các dạng bài tập thường gặp
Dạng 1. Vô nghiệm.
Ví dụ: Giải phương trình: $\sin x = 2$.
Giải
Do |2|>1 nên phương trình vô nghiệm.
Dạng 2. $\sin x = m$, với m là các giá trị đặc biệt: $m =$ { 0; $\pm 1$; $\pm \frac{1}{2}$;$ \pm \frac{{\sqrt 2 }}{2}$; $ \pm \frac{{\sqrt 3 }}{2}$; $\pm 1$ }.
Ví dụ: Giải phương trình: $\sin x = \frac{1}{2}$.
Nhận xét: Trước hết ta đặt: $\sin x = \frac{1}{2} = \sin \alpha $.
Để tìm được $\alpha $, ta sử dụng máy tính cầm tay fx570 VN Plus với lưu ý là: $\alpha = {\sin ^{ – 1}}\left( m \right)$. Trong trường hợp này, ta có: $\alpha = {\sin ^{ – 1}}\left( {\frac{1}{2}} \right) = \frac{\pi }{6}$. Từ đó phương trình được trình bày như sau.
Giải
$\begin{array}{l}
\sin x = \frac{1}{2} = \sin \frac{\pi }{6}\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{6} + k2\pi }\\
{x = \pi – \frac{\pi }{6} + k2\pi }
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{6} + k2\pi }\\
{x = \frac{{5\pi }}{6} + k2\pi }
\end{array}} \right.\left( {k \in Z} \right)
\end{array}$
Dạng 3. Phương trình: $\sin x = m$, với m là các giá trị không đặc biệt.
Ví dụ: Giải phương trình: $\sin x = \frac{1}{3}$.
Giải
$\sin x = \frac{1}{3} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \arcsin \left( {\frac{1}{3}} \right) + k2\pi }\\
{x = \pi – \arcsin \left( {\frac{1}{3}} \right) + k2\pi }
\end{array}} \right.$
Dạng 4. Phương trình: $\sin \left( {u\left( x \right)} \right) = \sin \alpha $.
Ví dụ: Giải phương trình: $\sin \left( {2x + \frac{\pi }{6}} \right) = \sin \frac{\pi }{5}$.
Giải
$\sin \left( {2x + \frac{\pi }{6}} \right) = \sin \frac{\pi }{5} \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {2x + \frac{\pi }{6} = \frac{\pi }{5} + k2\pi }\\ {2x + \frac{\pi }{6} = \pi – \frac{\pi }{5} + k2\pi } \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {2x = \frac{\pi }{{30}} + k2\pi }\\ {2x = \frac{{19\pi }}{{30}} + k2\pi } \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = \frac{\pi }{{60}} + k\pi }\\ {x = \frac{{19\pi }}{{60}} + k\pi } \end{array}} \right.$Dạng 5. Phương trình: $\sin \left( {u\left( x \right)} \right) = \cos \left( {v\left( x \right)} \right)$.
Phương pháp: $\sin \left( {u\left( x \right)} \right) = \cos \left( {v\left( x \right)} \right) \Leftrightarrow \sin \left( {u\left( x \right)} \right) = \sin \left( {\frac{\pi }{2} – v\left( x \right)} \right)$.
Ví dụ: Giải phương trình $\sin \left( {2x + \frac{\pi }{6}} \right) = \cos \left( {x – \frac{\pi }{3}} \right)$.
Giải
$\sin \left( {2x + \frac{\pi }{6}} \right) = \cos \left( {x – \frac{\pi }{3}} \right) \Leftrightarrow \sin \left( {2x + \frac{\pi }{6}} \right) = \sin \left( {\frac{\pi }{2} – x + \frac{\pi }{3}} \right) \Leftrightarrow \sin \left( {2x + \frac{\pi }{6}} \right) = \sin \left( {\frac{{5\pi }}{6} – x} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {2x + \frac{\pi }{6} = \frac{{5\pi }}{6} – x + k2\pi }\\ {2x + \frac{\pi }{6} = \pi – \frac{{5\pi }}{6} + x + k2\pi } \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {3x – = \frac{{2\pi }}{3} + k2\pi }\\ {x = k2\pi } \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}}\\ {x = k2\pi } \end{array}} \right.$Dạng 6. Tìm nghiệm thuộc khoảng, đoạn $\left[ {a;b} \right]$.
Ví dụ: Tìm nghiệm của phương trình: $\sin \left( {2x + \frac{\pi }{6}} \right) = 1$ thuộc đoạn [-1;1].
Giải
$\sin \left( {2x + \frac{\pi }{6}} \right) = 1 = \sin \frac{\pi }{2} \Leftrightarrow 2x + \frac{\pi }{6} = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{6} + k\pi $Theo giả thiết ta có:
$\begin{array}{l} – 1 \le x \le 1\\ \Leftrightarrow – 1 \le \frac{\pi }{6} + k\pi \le 1\\ \Leftrightarrow – 1 – \frac{\pi }{6} \le k\pi \le 1 – \frac{\pi }{6}\\ \Leftrightarrow – \frac{1}{\pi } – \frac{1}{6} \le k \le \frac{1}{\pi } – \frac{1}{6} \end{array}$Vì $k \in Z$ suy ra $k = 0$. Vậy nghiệm cần tìm là: $\frac{\pi }{6}$.
Dạng 7. Phương trình có ẩn ở mẫu: $\frac{{f(x)}}{{g(x)}} = 0$.
Phương pháp.
- Bước 1: Tìm điều kiện xác định của phương trình, $g(x) \ne 0$.
- Bước 2: Giải phương trình f(x)=0.
- Bước 3: Loại nghiệm.
- Bước 4: Kết luận
Ví dụ: Giải phương trình: $\frac{{\sin 3x}}{{\cos x – 1}} = 0$
Giải
- Điều kiện: $\cos x \ne 1 \Leftrightarrow x \ne k2\pi $ (1).
- $pt \Leftrightarrow \sin 3x = 0 \Leftrightarrow 3x = k\pi \Leftrightarrow x = k\frac{\pi }{3}$ (2).
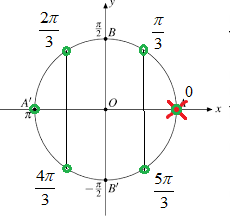
Biểu diễn (1) (dấu nhân đỏ) và (2) (dấu tròn xanh) trên cùng một đường tròn lượng giác bằng cách cho k=1;2;3;4;5;6;… (Hình vẽ). Ta thấy dấu nhân đỏ và tròn xanh trùng nhau khi k=0;6;12;…;6m;… Các giá trị lượng giác tại đó bị loại.
Vậy: Phương trình có nghiệm: $x = \frac{\pi }{3} + k\pi $; $x = \frac{{2\pi }}{3} + k\pi $; $x = (2k + 1)\pi $.
II. Phương trình cosx= m
- Nếu \(|m|>1\): Phương trình vô nghiệm.
- Nếu \(|m|\leq 1\):
- \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \left( {k \in\mathbb{Z} } \right)\)
- \(\cos x = \cos {\beta ^0} \Leftrightarrow x = \pm {\beta ^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)\)
- \(\cos x = a \Leftrightarrow x = \pm \,arcc{\rm{os}}a + k2\pi \left( {k \in \mathbb{Z}} \right)\)
- Tổng quát: \(\cos f\left( x \right) =\cos g\left( x \right) \Leftrightarrow f\left( x \right) = \pm g\left( x \right) + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
- Các trường hợp đặc biệt:
\(\begin{array}{l} \oplus \,\,\,\cos x = 1 \Leftrightarrow x = k2\pi \,\,\,\left( {k \in\mathbb{Z} } \right)\\ \oplus \,\,\,\cos x = – 1 \Leftrightarrow x = \pi + k2\pi \,\,\,\left( {k \in\mathbb{Z} } \right)\\ \oplus \,\,\,\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right) \end{array}\)
Lưu ý: Các dạng bài tập của cosx=m giống như của sinx=m.
III. Phương trình tanx= m
\(\begin{array}{l} \oplus \tan x = {\mathop{\rm t}\nolimits} {\rm{an}}\alpha \Leftrightarrow \,x\,{\rm{ = }}\,\alpha + k\pi \,\,\,\,\left( {k \in\mathbb{Z} } \right)\\ \oplus \tan x = {\mathop{\rm t}\nolimits} {\rm{an}}{\beta ^0} \Leftrightarrow \,x{\rm{ = }}{\beta ^0} + k{\rm{18}}{{\rm{0}}^0}\,\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \oplus \tan x = a \Leftrightarrow x{\rm{ = }}\arctan a\, + k\pi \,\,\,\,\left( {k \in\mathbb{Z} } \right) \end{array}\)
Tổng quát: \(\tan f\left( x \right) = \tan g\left( x \right) \Leftrightarrow f\left( x \right) = g\left( x \right) + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
Ví dụ: Giải phương trình: $\tan x = \sqrt 3 $.
Giải
$\begin{array}{l}
\tan x = \sqrt 3 = \tan \frac{\pi }{3}\
\Leftrightarrow x = \frac{\pi }{3} + k\pi
\end{array}$.
IV. Phương trình cotx=a
\(\begin{array}{l} \oplus \cot x = \cot \alpha \Leftrightarrow {\rm{x}}\,\,{\rm{ = }}\,\alpha \,{\rm{ + }}\,{\rm{k}}\pi \,\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \oplus \cot x = \cot {\beta ^0} \Leftrightarrow {\rm{x}}\,\,{\rm{ = }}\,{\beta ^0}{\rm{ + }}\,{\rm{k18}}{{\rm{0}}^0}\,\,\,\,\left( {k \in\mathbb{Z} } \right)\\ \oplus \cot x = a \Leftrightarrow {\rm{x}}\,\,{\rm{ = }}{\mathop{\rm arc}\nolimits} \cot \,a\,{\rm{ + }}\,{\rm{k}}\pi \,\,\,\,\left( {k \in\mathbb{Z} } \right) \end{array}\)
Tổng quát: \(\cot f\left( x \right) = \cot g\left( x \right) \Leftrightarrow f\left( x \right) = g\left( x \right) + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
Lưu ý: $\cot x = m \Leftrightarrow \tan x = \frac{1}{m}$.
Ví dụ: Giải phương trình: $\cot x = – \sqrt 3 $.
Giải
$\begin{array}{l}
\cot x = – \sqrt 3 \
\Leftrightarrow \tan x = – \frac{1}{{\sqrt 3 }} = \tan \left( { – \frac{\pi }{6}} \right)\
\Leftrightarrow x = – \frac{\pi }{6} + k\pi
\end{array}$.
Một số bài tập minh họa
Ví dụ 1
Giải các phương trình sau:
a) \(\sin \left( {\frac{{2x}}{3} – \frac{\pi }{3}} \right)=0\).
b) \(\sin x = \sin \frac{\pi }{{12}}\).
c) \(\sin 3x = \frac{1}{2}\).
d) \(\sin x = \frac{2}{3}\).
Lời giải:
a) \(\sin \left( {\frac{{2x}}{3} – \frac{\pi }{3}} \right)=0\Leftrightarrow \frac{{2x}}{3} – \frac{\pi }{3} = k\pi \Leftrightarrow \,\frac{{2x}}{3} = \frac{\pi }{3} + k\pi\)
\(\Leftrightarrow \,x = \frac{\pi }{2} + k\frac{{3\pi }}{2}\), \(k \in \mathbb{Z}.\)
Vậy phương trình có các nghiệm là: \(\,x = \frac{\pi }{2} + k\frac{{3\pi }}{2}\), \(k \in \mathbb{Z}.\)
b) \(\sin x = \sin \frac{\pi }{{12}} \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{{12}} + k2\pi \\ x = \pi – \frac{\pi }{{12}} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{{12}} + k2\pi \\ x = \frac{{11\pi }}{{12}} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình có các nghiệm là \(x = \frac{\pi }{{12}} + k2\pi ,k\in \mathbb{Z}\) và \(x = \frac{11\pi }{{12}} + k2\pi ,k\in \mathbb{Z}.\)
c) \(\sin 3x = \frac{1}{2} \Leftrightarrow \sin 3x = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l} 3x = \frac{\pi }{6} + k2\pi \\ 3x = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \frac{\pi }{{18}} + k\frac{{2\pi }}{3}\\ x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3} \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình có các nghiệm là \(x = \frac{\pi }{{18}} + k\frac{{2\pi }}{3}, k \in \mathbb{Z}\) và \(x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}, k \in \mathbb{Z}\).
d) \(\sin x = \frac{2}{3} \Leftrightarrow \left[ \begin{array}{l} x = \arcsin \frac{2}{3} + k2\pi \\ x = \pi – \arcsin \frac{2}{3} + k2\pi \end{array} \right.\left( {k \in\mathbb{Z} } \right)\)
Vậy phương trình có các nghiệm là \(x = \arcsin \frac{2}{3} + k2\pi,k \in \mathbb{Z}\) và \(x = \pi – \arcsin \frac{2}{3} + k2\pi, k \in \mathbb{Z}.\)
Ví dụ 2
Giải các phương trình sau:
a) \(\cos \left( {\frac{{3x}}{2} – \frac{\pi }{4}} \right) = – \frac{1}{2}\).
b) \(\cos \left( {x + {{45}^0}} \right) = \frac{{\sqrt 2 }}{2}\).
Lời giải
a) \(\cos \left( {\frac{{3x}}{2} – \frac{\pi }{4}} \right) = – \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l} \frac{{3x}}{2} – \frac{\pi }{4} = \frac{{2\pi }}{3} + k2\pi \\ \frac{{3x}}{2} – \frac{\pi }{4} = – \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)\(\Leftrightarrow \left[ \begin{array}{l} x = \frac{{11\pi }}{{18}} + k\frac{{4\pi }}{3}\\ x = – \frac{{5\pi }}{{18}} + k\frac{{4\pi }}{3} \end{array} \right.{\mkern 1mu} ,{\mkern 1mu} k \in \mathbb{Z}.\)
Vậy phương trình có các nghiệm là: \({x = \frac{{11\pi }}{{18}} + k\frac{{4\pi }}{3}}, k \in \mathbb{Z}\) và \({x = – \frac{{5\pi }}{{18}} + k\frac{{4\pi }}{3}}, k \in \mathbb{Z}.\)
b) \(\cos \left( {x + {{45}^0}} \right) = \frac{{\sqrt 2 }}{2} \Leftrightarrow \cos \left( {x + {{45}^0}} \right) = c{\rm{os}}{45^0}\)
\(\Leftrightarrow \left[ \begin{array}{l} x + {45^0} = {45^0} + k{360^0}\\ x + {45^0} = – {45^0} + k{360^0} \end{array} \right.\)\(\Leftrightarrow \left[ \begin{array}{l} x = {45^0} + k{360^0}\\ x = – {90^0} + k{360^0} \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)
Vậy phương trình có các nghiệm là: \({x = {{45}^0} + k{{360}^0}}, k \in \mathbb{Z}\) và \({x = – {{90}^0} + k{{360}^0}}, k \in \mathbb{Z}.\)
Ví dụ 3
Giải các phương trình sau:
a) \(\tan x = \tan \frac{\pi }{3}\).
b) \(\tan (x – {15^0}) = \frac{{\sqrt 3 }}{3}\).
Lời giải
a) \(\tan x = \tan \frac{\pi }{3} \Leftrightarrow x = \frac{\pi }{3} + k\pi ,\left( {k \in\mathbb{Z} } \right).\)
b) \(\tan (x – {15^0}) = \frac{{\sqrt 3 }}{3} \Leftrightarrow\) \(\tan (x – {15^0}) = \tan {30^0}\Leftrightarrow x = {45^0} + k{180^0} , k \in \mathbb{Z}.\)
Vậy các nghiệm của phương trình là \(x = {45^0} + k{180^0} , k \in \mathbb{Z}.\)
Ví dụ 4
Giải các phương trình sau:
a) \(\cot 4x = \,\cot \frac{{2\pi }}{7}\).
b) \(\cot 4x = – 3.\)
c) \(\cot \left( {2x – \frac{\pi }{6}} \right) = \frac{1}{{\sqrt 3 }}\).
Lời giải
a) \(\cot 4x = \,\cot \frac{{2\pi }}{7}\) \(\Leftrightarrow 4x = \frac{{2\pi }}{7}\, + \,k\pi \Leftrightarrow \,x = \frac{\pi }{{14}} + \,k\frac{\pi }{4},\,k \in \mathbb{Z}.\)
Vậy các nghiệm của phương trình là: \(x = \frac{\pi }{{14}} + \,k\frac{\pi }{4};\,k \in \mathbb{Z}.\)
b) \(\cot 4x = – 3 \Leftrightarrow 4x = \arctan \left( { – 3} \right) + k\pi \Leftrightarrow x = \frac{1}{4}\arctan \left( { – 3} \right) + k\frac{\pi }{4},\left( {k \in \mathbb{Z}} \right).\)
Vậy các nghiệm của phương trình là: \(x = \frac{1}{4}\arctan \left( { – 3} \right) + k\frac{\pi }{4},\left( {k \in \mathbb{Z}} \right).\)
c) \(\cot \left( {2x – \frac{\pi }{6}} \right) = \frac{1}{{\sqrt 3 }} \Leftrightarrow \cot \left( {2x – \frac{\pi }{6}} \right) = \cot \frac{\pi }{6}\)
\(\Leftrightarrow 2x – \frac{\pi }{6} = \frac{\pi }{6} + k\pi \Leftrightarrow 2x = \frac{\pi }{3} + k\pi\)
\(\Leftrightarrow x = \frac{\pi }{6} + k\frac{\pi }{2},\left( {k \in\mathbb{Z} } \right).\)
Vậy các nghiệm của phương trình là: \(x = \frac{\pi }{6} + k\frac{\pi }{2},\left( {k \in\mathbb{Z} } \right).\)
Bài tập Trắc nghiệm
-
Câu 1: Phương trình \(\sin 4x = \sin \frac{\pi }{5}\) có nghiệm?
- A. \(x = \frac{\pi }{{20}} + k\frac{\pi }{2};x = \frac{\pi }{5} + k\frac{\pi }{2},k \in \mathbb{Z}.\)
- B. \(x = \frac{\pi }{{20}} + k\frac{\pi }{2};x = \frac{\pi }{{10}} + k\frac{\pi }{2},k \in \mathbb{Z}.\)
- C. \(x = \frac{\pi }{{10}} + k\frac{\pi }{2};x = \frac{\pi }{5} + k\frac{\pi }{2},k \in \mathbb{Z}.\)
- D. \(x = \frac{{3\pi }}{5} + k\frac{\pi }{2};x = \frac{\pi }{{10}} + k\frac{\pi }{2},k \in \mathbb{Z}.\)
-
Câu 2: Phương trình \(\cos \left( {x + \frac{\pi }{{18}}} \right) = \frac{2}{5}\) có nghiệm?
- A. \(x = \pm \arccos \frac{2}{5} – \frac{\pi }{{18}} + k2\pi ,k \in \mathbb{Z}.\)
- B. \(x = \pm \arccos \frac{2}{5} + \frac{\pi }{{18}} + k2\pi ,k \in \mathbb{Z}.\)
- C. \(x = \pm \arccos \frac{5}{2} – \frac{\pi }{{18}} + k2\pi ,k \in \mathbb{Z}.\)
- D. \(x = \pm \arccos \frac{5}{2} + \frac{\pi }{{18}} + k2\pi ,k \in \mathbb{Z}.\)
-
- A. \({x_1} = 5 – \frac{{11\pi }}{6};{x_2} = 5 – \frac{{13\pi }}{6}.\)
- B. \({x_1} = 5 + \frac{{11\pi }}{6};{x_2} = 5 – \frac{{13\pi }}{6}.\)
- C. \({x_1} = 5 – \frac{{11\pi }}{6};{x_2} = 5 + \frac{{13\pi }}{6}.\)
- D. \({x_1} = 5 + \frac{{11\pi }}{6};{x_2} = 5 + \frac{{13\pi }}{6}.\)
…………………………………….
Xem thêm:
- Phương trình lượng giác cơ bản
- Phương trình lượng giác thường gặp-Phần 1.
- Phương trình lượng giác thường gặp-Phần 2.
- Phương trình lượng giác- Phương pháp nhóm nhân tử chung.
- Phương trình lượng giác- Phương pháp đặt ẩn phụ.
- Phương trình lượng giác- Phương pháp bất đẳng thức.
- Phương trình lượng giác-Phương pháp tổng bình phương.



0 Bình luận