Quy tắc tính đạo hàm

Quy tắc tính đạo hàm

I. ĐẠO HÀM HÀM SỐ THƯỜNG GẶP

Định lí 1.

Hàm số hằng $y=C$ có đạo hàm (C)’=0.

Định lí 2.

Hàm số $y=x$ có đạo hàm tại mọi x thuộc R và (x)’=1.

Chứng minh

Ta có: $\mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x + \Delta x) – f(x)}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{x + \Delta x – x}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} (1) = 1$. Suy ra: (x)’=1, $\forall x \in R$.

Định lý 3

Hàm số $y=x^n$ có đạo hàm với mọi $x \in R$, với mọi $n \in {N^*}$ và $\left( {{x^n}} \right)’ = n{x^{n – 1}}$.

Chứng minh

Cho x số gia $\Delta x \ne 0$. Ta có:

$y’\left( x \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x + \Delta x) – f(x)}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{\left( {x – \Delta x} \right)}^n} – {x^n}}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{\left( {x – \Delta x} \right)}^n} – {x^n}}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta x\left[ {{{\left( {x – \Delta x} \right)}^{n – 1}} + {{\left( {x – \Delta x} \right)}^{n – 2}}.x + {{\left( {x – \Delta x} \right)}^{n – 3}}.{x^2} + … + {x^{n – 1}}} \right]}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \left[ {{{\left( {x – \Delta x} \right)}^{n – 1}} + {{\left( {x – \Delta x} \right)}^{n – 2}}.x + {{\left( {x – \Delta x} \right)}^{n – 3}}.{x^2} + … + {x^{n – 1}}} \right]$

$ = n.{x^{n – 1}}$. (đpcm)

Định lý 4

Hàm số $y=\sqrt x$ có đạo hàm với mọi x dương và $\left( {\sqrt x } \right)’ = \frac{1}{{2\sqrt x }}$.

Chứng minh

Cho x dương số gia $\Delta x \ne 0$. Ta có:

$\left( {\sqrt x } \right)’ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f(x + \Delta x) – f(x)}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sqrt {x + \Delta x} – \sqrt x }}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta x}}{{\Delta x\left( {\sqrt {x + \Delta x} + \sqrt x } \right)}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{1}{{\left( {\sqrt {x + \Delta x} + \sqrt x } \right)}}$

$ = \frac{1}{{2\sqrt x }}$.

II. CÔNG THỨC TÍNH ĐẠO HÀM

Định lí 5.

Giả sử các hàm số $u=u(x)$, $v=v(x)$ là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định, ta có:

• $(u+v)’=u’+v’$.
• $(u-v)’=u’-v’$.
• $(u.v)’=u’v-uv’$.
• $\left( {\frac{u}{v}} \right)’ = \frac{{u’v – uv’}}{{{v^2}}}$;$\left( {v\left( x \right) \ne 0} \right)$.

Chứng minh

• Xét y=u+v. Cho x số gia $\Delta x \ne 0$. Khi đó ${\Delta u}$ và ${\Delta v}$ là số gia hàm số tương ứng với ${\Delta x}$ của hàm u và v. Ta có:

$(u + v)’ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\left[ {\left( {u + \Delta u} \right) + \left( {v + \Delta v} \right)} \right] – \left( {u + v} \right)}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta u + \Delta v}}{{\Delta x}}$

$ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta u}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta v}}{{\Delta x}} = u’ + v’$. (đpcm).

Tương tự : $\left( {u – v} \right)’ = u’ – v’$.

Mở rộng: $\left( {u \pm v \pm … \pm {\rm{w}}} \right)’ = u’ \pm v’ \pm … \pm {\rm{w}}’$.

Hệ quả

• $\left( {k.u} \right)’ = k.u’;\forall k \in R.$
• $\left( {\frac{k}{u}} \right)’ = – k.\frac{{u’}}{{{u^2}}};\forall k \in R.$

III. ĐẠO HÀM HÀM SỐ HỢP

3.1. Định nghĩa hàm hợp

Giả sử

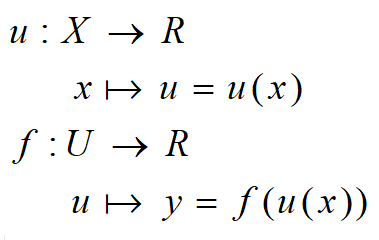
Khi đó ta gọi hàm số $y=f(u)$ là hàm số hợp của biến số x qua biến trung gian u và $y = f(u(x))$.

Ví dụ 1: Hàm số $y=u^5$ và $u=1-x^3$. Khi đó: Hàm số $y=f(u(x))=(1-x^3)^5$.

Ví dụ 2: Hàm số $y=\sqrt u$ và $u=x^3+2x+1$. Khi đó: Hàm số $y = f(u(x)) = \sqrt {{x^3} + 2x + 1} $

3.2. Đạo hàm hàm hợp

Định lý 6

Nếu hàm số $u = u(x)$ có đạo hàm tại x là ${{u’}_x}$ và hàm số $y = f(u)$ có đạo hàm tại u là ${{y’}_u}$ thì hàm hợp $y = f(u(x))$ có đạo hàm tại x và ${{y’}_x} = {{y’}_u}.{{u’}_x}$ .

Hệ quả

• $\left( {{u^n}} \right)’ = n.{u^{n – 1}}.u’$

• $\left( {\sqrt u } \right)’ = \frac{{u’}}{{2\sqrt u }}$

• $\left( {\frac{{ax + b}}{{cx + d}}} \right)’ = \frac{{ac – bd}}{{{{\left( {cx + d} \right)}^2}}};\left( {c \ne 0;ad \ne cb} \right)$

Tổng hợp 10 công thức đạo hàm thường gặp

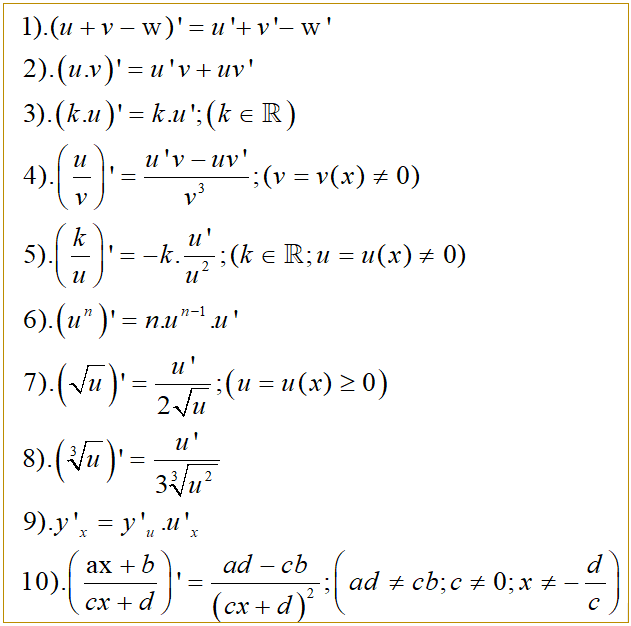
IV. Luyện tập

Ví dụ 1.

Tính y’ với $y = \sqrt {{x^2} + x + 1} $.

Giải

$y’ = {\rm{ }}\left( {\sqrt {{x^2} + x + 1} } \right){\rm{‘}} = {\rm{ }}\frac{{\left( {{x^2} + x + 1} \right)}}{{2\sqrt {{x^2} + x + 1} }} = \frac{{2x + 1}}{{2\sqrt {{x^2} + x + 1} }}$

Ví dụ 2.

Tính y’ biết $y = \frac{{x + 1}}{{\sqrt {x – 1} }}$

Giải

$ y’= \frac{{\left( {x + 1} \right)’\sqrt {x – 1} – (x + 1)\left( {\sqrt {x – 1} } \right)’}}{{{{\left( {\sqrt {x – 1} } \right)}^2}}}$

$ = \frac{{\sqrt {x – 1} – \left( {x + 1} \right)\frac{{\left( {x – 1} \right)’}}{{2\sqrt {x – 1} }}}}{{x – 1}}$

$ = \frac{{\sqrt {x – 1} – \frac{{(x + 1)}}{{2\sqrt {x – 1} }}}}{{x – 1}}$

$ = \frac{{2(x – 1) – (x + 1)}}{{2(x – 1)\sqrt {x – 1} }}$

$ = \frac{{x – 3}}{{2{{\left( {\sqrt {x – 1} } \right)}^3}}};\left( {x > 1} \right)$.