SỐ PHỨC

I. KIẾN THỨC CẦN NHỚ:

1. Định nghĩa số phức

Định nghĩa:
· Một số phức là một biểu thức dạng z=a+bi với $a,b\in \mathbb{R}$ và ${{i}^{2}}=-1$, trong đó: $i$ được gọi là đơn vị ảo, a được gọi là phần thực và b được gọi là phần ảo của số phức: z=a+bi
· Tập hợp các số phức được kí hiệu là $\mathbb{C}$. $\mathbb{C}=\left\{ a+bi/a,b\in \mathbb{R};{{i}^{2}}=-1 \right\}$.

· Chú ý:

– Khi phần ảo $b=0\Leftrightarrow z=a$ là số thực.

– Khi phần thực $a=0\Leftrightarrow z=bi\Leftrightarrow z$ là số thuần ảo.

– Số $0=0+0i$ vừa là số thực, vừa là số ảo.

2. Hai số phức bằng nhau, đối nhau

$ \cdot $ Hai số phức bằng nhau: $a + bi = c + di \Leftrightarrow {\rm{ }}\left\{ {\begin{array}{*{20}{c}} {a = c}\\ {b = d} \end{array}} \right.$ với $a,b,c,d\in \mathbb{R}$.

· Hai số phức ${{z}_{1}}=a+bi;\text{ }{{z}_{2}}=-a-bi$ được gọi là hai số phức đối nhau.

+ Các tập số: $\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}$.

3. Số phức liên hợp.

· Số phức liên hợp của $z=a+bi$ với $a,b\in \mathbb{R}$ là $a-bi$ và được kí hiệu bởi $\overline{z}$ . Rõ ràng $\overline{\overline{z}}=z$

4. Biểu diễn hình học.

· Trong mặt phẳng phức Oxy (Ox là trục thực, Oy là trục ảo ), số phức $z=a+bi$ với $a,b\in \mathbb{R}$ được biểu diễn bằng điểm $M\left( a;b \right)$.

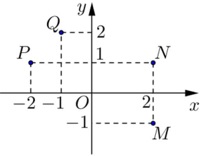
$\begin{array}{l} P( – 2;1) \Rightarrow {z_1} = – 2 + i\\ Q( – 1;2) \Rightarrow {z_2} = – 1 + 2i\\ N(2;1) \Rightarrow {z_3} = 2 + i\\ M(2; – 1) \Rightarrow {z_4} = 2 – i \end{array}$

5. Mô đun của số phức.

· Môđun của số phức $z=a+bi\text{ }\left( a,b\in \mathbb{R} \right)$ là $\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}$.

Ví dụ: $z = – 2 + i \Rightarrow \left| z \right| = \sqrt {{{\left( { – 2} \right)}^2} + {1^2}} = \sqrt 5 .$

Các tính chất:

.$\centerdot \left| z.{z}’ \right|=\left| z \right|\left| {{z}’} \right|$

· $\left| \frac{z}{{{z}’}} \right|=\frac{\left| z \right|}{\left| {{z}’} \right|}$

· $\left| \left| z \right|-\left| {{z}’} \right| \right|\le \left| z+{z}’ \right|\le \left| z \right|+\left| {{z}’} \right|$

· $\left| \left| z \right|-\left| {{z}’} \right| \right|\le \left| z-{z}’ \right|\le \left| z \right|+\left| {{z}’} \right|$

6. Các phép toán trên tập số phức.

Cho hai số phức: $z=a+bi; z’=a’+b’i\text{ }$ với $a,b,a’,b’\in \mathbb{R}$ và số $k\in \mathbb{R}$.

· Tổng hai số phức: $z+z’=a+a’+(b+b’)i$.

· Hiệu hai số phức: $z-z’=a-a’+(b-b’)i\text{ }\text{.}$

· Nhân hai số phức: $z.z’=\left( a+bi \right)\left( a’+b’i \right)=\left( a.a’-b.b’ \right)+\left( a.b’+a’.b \right)i$.

·Nhân một số với một số phức: $\centerdot k.z=k.(a+bi)=ka+kbi$.

· Nếu $z\ne 0$ thì $\frac{z’}{z}=\frac{z’.\overline{z}}{{{\left| z \right|}^{2}}}$, nghĩa là nếu muốn chia số phức $z’$ cho số phức $z\ne 0$ thì ta nhân cả tử và mẫu của thương $\frac{z’}{z}$ cho $\overline{z}$.

$\frac{{{z_1}}}{{{z_2}}} = \frac{{{z_1}.{{\bar z}_2}}}{{{z_2}.{{\bar z}_2}}} = \frac{{{z_1}.{{\bar z}_2}}}{{{{\left| {{z_2}} \right|}^2}}} = \frac{{\left( {a + b.i} \right).\left( {a’ – b’.i} \right)}}{{{a’^2} + {b’^2}}} = \frac{{\left( {aa’ + bb’} \right) + \left( {ba’ – ab’} \right)i}}{{{a’^2} + {b’^2}}} = \frac{{aa’ + bb’}}{{{a’^2} + {b’^2}}} + \frac{{ba’ – ab’}}{{{a’^2} + {b’^2}}}i.$

7. Lũy thừa của đơn vị ảo

Ta có:

$\begin{array}{l} \cdot {i^1} = i\\ \cdot {i^2} = – 1\\ \cdot {i^3} = – i\\ \cdot {i^4} = 1\\ \cdot {i^5} = i\\ \cdot {i^6} = – 1\\ \cdot {i^7} = – i\\ \cdot {i^8} = 1 \end{array}$

Từ phân tích trên, ta có:

$\begin{array}{l} \cdot {i^{4k}} = 1\\ \cdot {i^{4k + 1}} = i\\ \cdot {i^{4k + 2}} = – 1\\ \cdot {i^{4k + 3}} = – i;\forall k \in \mathbb{N}. \end{array}$

8. Căn bậc 2 của số thực âm.

· Căn bậc hai của số thực a âm là $\pm i\sqrt{\left| a \right|}$.

9. Giải phương trình bậc 2 trên tập số phức.

Cho phương trình bậc 2: $a{{z}^{2}}+bz+c=0\text{ }(1)$ Trong đó $a,b,c$ là những số thực và $a\ne 0$.

· Xét biệt thức: $\Delta = {b^2} – 4ac$ .

· Nếu $\Delta >0$ thì phương trình (1) có 2 nghiệm thực phân biệt: ${x_{1/2}} = \frac{{ – b \pm \sqrt \Delta }}{{2a}}$.

· Nếu $\Delta <0$ thì phương trình (1) có 2 nghiệm phức phân biệt: ${x_{1/2}} = \frac{{ – b \pm i\sqrt \Delta }}{{2a}}$.

· Nếu $\Delta =0$ thì phương trình (1) có nghiệm kép: ${x_{1/2}} = \frac{{ – b}}{{2a}}$.

II. PHÂN DẠNG BÀI TẬP

Thực hiện các phép toán.
- Tìm phần thực, phần ảo.
- Số phức liên hợp.
- Tính mô đun của số phức.
Phương trình trên tập phức.
Biểu diễn một số phức-tập hợp điểm.
Tìm số phức thỏa mãn điều kiện cho trước.
Cực trị của số phức.

III. Ví dụ minh họa

Ví dụ 1.

Cho số phức $z$ thoả mãn $\frac{z}{3+2i}=1-i$ Số phức liên hợp $\bar{z}$ là.

A. $\bar{z}=5+i$. B. $\bar{z}=-5-i$. C. $\bar{z}=-1-5i$. D. $\bar{z}=-1+5i$.

Lời giải

Chọn A

$z=\left( 3+2i \right)\left( 1-i \right)=5-i$.

Số phức liên hợp $\bar{z}=5+i$.

Ví dụ 2.

Cho hai số phức $z=1+3i$, $w=2-i$. Tìm phần ảo của số phức $u=\overline{z}.w$.

A. $5$. B. $-7i$. C. $-7$. D. $5i$.

Lời giải.

Chọn C

$\overline{z}=1-3i$; $u=\overline{z}.\text{w}=\left( 1-3i \right)\left( 2-i \right)=-1-7i$.

Vậy phần ảo của số phức $u$ bằng $-7$.

Ví dụ 3.

Gọi ${{z}_{1}}$; ${{z}_{2}}$ là các nghiệm của phương trình ${{z}^{2}}-3z+5=0$. Mô đun của số phức $\left( 2\overline{{{z}_{1}}}-3 \right)\left( 2\overline{{{z}_{2}}}-3 \right)$ bằng

A. $7$. B. $11$. C. $29$. D. $1$.

Lời giải.

Chọn B

Phương trình ${{z}^{2}}-3z+5=0$ có nghiệm là $z=\frac{3}{2}\pm \frac{\sqrt{11}}{2}i$

Không mất tính tổng quát, giả sử: ${{z}_{1}}=\frac{3}{2}+\frac{\sqrt{11}}{2}i$ và ${{z}_{2}}=\frac{3}{2}-\frac{\sqrt{11}}{2}i$

Ta có: $\left( 2\overline{{{z}_{1}}}-3 \right)\left( 2\overline{{{z}_{2}}}-3 \right)=\left( 3-i\sqrt{11}-3 \right)\left( 3+i\sqrt{11}-3 \right)=\left( -i\sqrt{11} \right)\cdot i\sqrt{11}=-11{{i}^{2}}=11$

Vậy mô đun của số phức $\left( 2\overline{{{z}_{1}}}-3 \right)\left( 2\overline{{{z}_{2}}}-3 \right)$ bằng $11$.

Ví dụ 4.

Cho số phức $z={{\left( \frac{2+6i}{3-i} \right)}^{m}},\,$$m$ nguyên dương. Có bao nhiêu giá trị $m\in \left[ 1;10 \right]$ để $z$ là số thuần ảo?

A. 2. B. 3. C. 5. D. 10.

Lời giải

Chọn C

Ta có: $z={{\left( \frac{2+6i}{3-i} \right)}^{m}}={{(2i)}^{m}}={{2}^{m}}.{{i}^{m}}\,$

$z$ là số thuần ảo khi và chỉ khi $m=2k+1,\,\,k\in \mathbb{N}$ (do $z\ne 0;\text{ }\forall m\in {{\mathbb{N}}^{*}}$).

Vậy có 5 giá trị $m$ thỏa yêu cầu đề bài.

Ví dụ 5.

Cho hai số phức ${{z}{1}}$, ${{z}{2}}$ thỏa mãn $\left| {{z}{1}} \right|=1$, $\left| {{z}{2}} \right|=2$ và $\left| {{z}{1}}+{{z}{2}} \right|=3$. Giá trị của $\left| {{z}{1}}-{{z}{2}} \right|$ là:
A. $0$.

B. $1$.

C. $2$.

D. $3$.
Lời giải
Chọn B
Giả sử ${{z}{1}}={{a}{1}}+{{b}{1}}i,\,\,\,\,\left( {{a}{1}},\,\,{{b}{1}}\in \mathbb{R} \right)$, ${{z}{2}}={{a}{2}}+{{b}{2}}i,\,\,\,\,\left( {{a}{2}},\,\,{{b}{2}}\in \mathbb{R} \right)$.
Theo bài ra ta có:

$\left\{ \begin{align} & \left| {{z}_{1}} \right|=1 \\ & \left| {{z}_{2}} \right|=2 \\ & \left| {{z}_{1}}+{{z}_{2}} \right|=3 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & a_{1}^{2}+b_{1}^{2}=1 \\ & a_{2}^{2}+b_{2}^{2}=4 \\ & {{\left( {{a}_{1}}+{{a}_{2}} \right)}^{2}}+{{\left( {{b}_{1}}+{{b}_{2}} \right)}^{2}}=9 \\ \end{align} \right.$ $\Leftrightarrow \left\{ \begin{align} & a_{1}^{2}+b_{1}^{2}=1 \\ & a_{2}^{2}+b_{2}^{2}=4 \\ & 2{{a}_{1}}{{a}_{2}}+2{{b}_{1}}{{b}_{2}}=4 \\ \end{align} \right.$.

Khi đó, ta có:
$\left| {{z}{1}}-{{z}{2}} \right|=\sqrt{{{\left( {{a}{1}}-{{a}{2}} \right)}^{2}}+{{\left( {{b}{1}}-{{b}{2}} \right)}^{2}}}$ $=\sqrt{\left( a_{1}^{2}+b_{1}^{2} \right)+\left( a_{2}^{2}+b_{2}^{2} \right)-\left( 2{{a}{1}}{{a}{2}}+2{{b}{1}}{{b}{2}} \right)}$ $=1$.
Vậy $\left| {{z}{1}}-{{z}{2}} \right|=1$.

Dạng 1. Tìm số phức

Câu 1. (Mã 104 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 3-i \right)=5x-4i$ với $i$ là đơn vị ảo.

A. $x=-1;y=-1$.

B. $x=-1;y=1$.

C. $x=1;y=-1$.

D. $x=1;y=1$.

Câu 2. (Mã 105 2017) Tìm tất cả các số thực $x,y$ sao cho ${{x}^{2}}-1+yi=-1+2i$.

A. $x=\sqrt{2},\,\,y=2$

B. $x=-\sqrt{2},\,\,y=2$

C. $x=0,\,\,y=2$

D. $x=\sqrt{2},\,\,y=-2$

Câu 3. (Mã 101 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 1-3i \right)=x+6i$ với $i$ là đơn vị ảo.

A. $x=1;y=-1$

B. $x=1;y=-3$

C. $x=-1;y=-3$

D. $x=-1;y=-1$

Câu 4. (Mã 104 – 2019) Cho số phức $z$ thỏa mãn $\left( 2-i \right)z+3+16i=2\left( \overline{z}+i \right)$. Môđun của $z$ bằng

A. $\sqrt{13}$.

B. $5$.

C. $\sqrt{5}$.

D. $13$.

Câu 5. (Mã 103 – 2019) Cho số $z$ thỏa mãn $\left( 2+i \right)z-4\left( \overline{z}-i \right)=-8+19i$. Môđun của $z$bằng

A. $13$.

B. $5$.

C. $\sqrt{13}$.

D. $\sqrt{5}$.

Câu 6. (Mã 102 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 3x+2yi \right)+\left( 2+i \right)=2x-3i$ với $i$ là đơn vị ảo.

A. $x=2;\,y=-2$

B. $x=2;\,y=-1$

C. $x=-2;\,y=-2$

D. $x=-2;\,y=-1$

Câu 7. (Đề Tham Khảo -2019) Tìm các số thực $a,b$ thỏa mãn $2a+(b+i)i=1+2i$ với $i$ là đơn vị ảo.

A. $a=0,b=1.$

B. $a=1,b=2.$

C. $a=0,b=2.$

D. $a=\frac{1}{2},b=1.$

Câu 8. (Mã 103 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 3x+yi \right)+\left( 4-2i \right)=5x+2i$ với $i$ là đơn vị ảo.

A. $x=2$; $y=4$

B. $x=-2$; $y=0$

C. $x=2$; $y=0$

D. $x=-2$; $y=4$

Câu 9. (Mã 102 – 2019) Cho số phức $z$ thoả mãn $3\left( \overline{z}-i \right)-\left( 2+3i \right)z=7-16i.$ Môđun của $z$ bằng

A. $3.$

B. $\sqrt{5}.$

C. $5.$

D. $\sqrt{3}.$

Câu 10. (Mã 101 – 2019) Cho số phức $z$ thỏa mãn $3\left( \overline{z}+i \right)-\left( 2-i \right)z=3+10i$. Môđun của $z$ bằng

A. $\sqrt{3}$.

B. $3$.

C. $5$.

D. $\sqrt{5}$.

Câu 11. (THPT Cẩm Giàng 2 Năm 2019) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 1-3i \right)=-1+6i$ với $i$ là đơn vị ảo.

A. $x=1$; $y=-3$.

B. $x=-1$; $y=-3$.

C. $x=-1$; $y=-1$.

D. $x=1$; $y=-1$.

Câu 12. Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 3-i \right)=5x-4i$ với $i$ là đơn vị ảo.

A. $x=-1,y=-1$

B. $x=1,y=1$

C. $x=-1,y=1$

D. $x=1,y=-1$

Câu 13. (Chuyên Sơn La 2019) Tìm các số thực $x$ và $y$ thỏa mãn $\left( 3x-2 \right)+\left( 2y+1 \right)i=\left( x+1 \right)-\left( y-5 \right)i$, 2với $i$ là đ7ơn vị ả4o.

A. $x=\frac{3}{2},\,y=-2$.

B. $x=-\frac{3}{2},\,y=-\frac{4}{3}$.

C. $x=1,\,y=\frac{4}{3}$.

D. $x=\frac{3}{2},\,y=\frac{4}{3}$.

Câu 14. (Chuyên Phan Bội Châu 2019) Cho số phức $z=a+bi\ \left( a,b\in \mathbb{R} \right)$ thỏa mãn $\left( 1+i \right)z+2\overline{z}=3+2i$. Tính $P=a+b$

A. $P=1$

B. $P=-\frac{1}{2}$

C. $P=\frac{1}{2}$

D. $P=-1$

Câu 15. (Chuyên KHTN -2019) Cho số phức $z$ thỏa mãn $\left( 2+3i \right)z+4-3i=13+4i$. Môđun của $z$ bằng

A. $2$.

B. $4$.

C. $2\sqrt{2}$.

D. $\sqrt{10}$.

Câu 16. (HSG Bắc Ninh 2019) Cho số phức $z=x+yi\,\,\left( x,y\in \mathbb{R} \right)$ thỏa mãn $\left( 1+2i \right)\overline{z}+z=3-4i$. Tính giá trị của biểu thức $S=3x-2y$.

A. $S=-12$

B. $S=-11$

C. $S=-13$

D. $S=-10$

Câu 17. (Sở Bình Phước 2019) Tổng phần thực và phần ảo của số phức $z$ thoả mãn $iz+\left( 1-i \right)\bar{z}=-2i$ bằng

A. $6$

B. $-2$

C. $2$

D. $-6$

Câu 18. (Sở Bình Phước 2019) Cho $a,\,b\in \mathbb{R}$ và thỏa mãn $\left( a+bi \right)i-2a=1+3i$, với $i$ là đơn vị ảo. Giá trị $a-b$ bằng

A. $4$

B. $-10$

C. $-4$

D. $10$

Câu 19. (Chuyen Phan Bội Châu Nghệ An 2019) Cho số phức $z=a+bi\text{ (}a,b\in \mathbb{R}\text{)}$ thoả mãn $(1+i)z+2\overline{z}=3+2i$. Tính $P=a+b$

A. $P=1$.

B. $P=-\frac{1}{2}$.

C. $P=\frac{1}{2}$.

D. $P=-1$

Câu 20. (Chuyên Hạ Long -2019) Tìm số phức $z$ biết $4z+5\overline{z}=27-7i$.

A. $z=-3+7i$.

B. $z=-3-7i$.

C. $z=3-7i$.

D. $z=3+7i$.

Câu 21. (THPT Lê Quý Đôn Đà Nẵng 2019) Cho số phức $z$ thỏa mãn $\left( 3+2i \right)z+{{\left( 2-i \right)}^{2}}=4+i$. Mô đun của số phức $w=\left( z+1 \right)\overline{z}$ bằng.

A. $2$.

B. $\sqrt{10}$.

C. $\sqrt{5}$.

D. $4$.

Câu 22. (THPT Lê Quý Đôn Đà Nẵng 2019) Tìm các số thực $a,b$ thỏa mãn$\left( a-2b \right)+\left( a+b+4 \right)i=\left( 2a+b \right)+2bi$ với $i$ là đơn vị ảo.

A. $a=-3,\,b=1$.

B. $a=3,\,b=-1$.

C. $a=-3,\,b=-1$.

D. $a=3,\,b=1$.

Câu 23. Cho hai số phức ${{z}_{1}}=m+1-2i$ và ${{z}_{1}}=2-\left( m+1 \right)i$. Có bao nhiêu giá trị thực của tham số $m$ để ${{z}_{1}}.\,{{z}_{2}}-8+8i$ là một số thực.

A. $1$.

B. $2$.

C. $3$.

D. $4$.

Câu 24. (Chuyên Bắc Giang 2019) Tìm mô đun của số phức$z$biết $\left( 2z-1 \right)\left( 1+i \right)+\left( \overline{z}+1 \right)\left( 1-i \right)=2-2i$.

A. $\frac{1}{9}$

B. $\frac{\sqrt{2}}{3}$

C. $\frac{2}{9}$

D. $\frac{1}{3}$

Câu 25. Tính mô đun của số phức $z$ thỏa mãn $z\left( 1+2i \right)+\overline{z}\left( 1-i \right)+4-i=0$ với $i$ là đơn vị ảo.

A. $\sqrt{6}$.

B. $\sqrt{5}$.

C. $\sqrt{2}$.

D. $\sqrt{3}$.

Hướng dẫn và lời giải

Câu 1.

(Mã 104 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 3-i \right)=5x-4i$ với $i$ là đơn vị ảo.

A. $x=-1;y=-1$.

B. $x=-1;y=1$.

C. $x=1;y=-1$.

D. $x=1;y=1$.

Lời giải
Chọn D

$\left( {2x – 3yi} \right) + \left( {3 – i} \right) = 5x – 4i \Leftrightarrow \left( {2x + 3} \right) – \left( {3y + 1} \right)i = 5x – 4i \Leftrightarrow \left\{ \begin{array}{l} 2x + 3 = 5x\\ 3y + 1 = 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = 1 \end{array} \right.$

Câu 2.

(Mã 105 2017) Tìm tất cả các số thực $x,y$ sao cho ${{x}^{2}}-1+yi=-1+2i$.

A. $x=\sqrt{2},\,\,y=2$

B. $x=-\sqrt{2},\,\,y=2$

C. $x=0,\,\,y=2$

D. $x=\sqrt{2},\,\,y=-2$

Lời giải
Chọn C

Từ ${{x}^{2}}-1+yi=-1+2i$

$ \Rightarrow \left\{ \begin{array}{l} {x^2} – 1 = – 1\\ y = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 0\\ y = 2 \end{array} \right.$

Câu 3.

(Mã 101 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 1-3i \right)=x+6i$ với $i$ là đơn vị ảo.

A. $x=1;y=-1$

B. $x=1;y=-3$

C. $x=-1;y=-3$

D. $x=-1;y=-1$

Lời giải
Chọn C

Ta có $\left( 2x-3yi \right)+\left( 1-3i \right)=x+6i$ $\Leftrightarrow x+1+\left( -3y-9 \right)i=0$

$ \Leftrightarrow \left\{ \begin{array}{l} x + 1 = 0\\ – 3y – 9 = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = – 1\\ y = – 3 \end{array} \right.$

Câu 4.

(Mã 104 – 2019) Cho số phức $z$ thỏa mãn $\left( 2-i \right)z+3+16i=2\left( \overline{z}+i \right)$. Môđun của $z$ bằng

A. $\sqrt{13}$.

B. $5$.

C. $\sqrt{5}$.

D. $13$.

Lời giải
Chọn A

Gọi $z=x+yi$.
$\left( 2-i \right)z+3+16i=2\left( \overline{z}+i \right)$
$\Leftrightarrow \left( 2-i \right)\left( x+yi \right)+3+16i=2\left( x-yi+i \right)$
$\Leftrightarrow 2x+2yi-xi+y+3+16i=2x-2yi+2i$

$ \Leftrightarrow \left\{ \begin{array}{l} 2x + y + 3 = 2x\\ 2y – x + 16 = – 2y + 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} y + 3 = 0\\ – x + 4y = – 14 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = 2\\ y = – 3 \end{array} \right.$

Suy ra $z=2-3i$. Vậy $\left| z \right|=\sqrt{13}$.

Câu 5.

(Mã 103 – 2019) Cho số $z$ thỏa mãn $\left( 2+i \right)z-4\left( \overline{z}-i \right)=-8+19i$. Môđun của $z$bằng

A. $13$.

B. $5$.

C. $\sqrt{13}$.

D. $\sqrt{5}$.

Lời giải
Chọn A

Gọi $z=a+bi\,\,;\,\,\overline{z}=a-bi\,\,\left( a,b\in \mathbb{R} \right).$
Ta có:

$\begin{array}{l} \left( {2 + i} \right)z – 4\left( {\bar z – i} \right) = – 8 + 19i\\ \Leftrightarrow \left( {2 + i} \right)\left( {a + bi} \right) – 4\left( {a – bi – i} \right) = – 8 + 19i\\ \Leftrightarrow – 2a – b + \left( {a + 6b + 4} \right) = – 8 + 19i\\ \Leftrightarrow \left\{ \begin{array}{l} – 2a – b = – 8\\ a + 6b + 4 = 19 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 3\\ b = 2 \end{array} \right. \end{array}$

Vậy $z=3+2i\,\,\Rightarrow \left| z \right|=\sqrt{13}\,.$

Câu 6.

(Mã 102 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 3x+2yi \right)+\left( 2+i \right)=2x-3i$ với $i$ là đơn vị ảo.

A. $x=2;\,y=-2$

B. $x=2;\,y=-1$

C. $x=-2;\,y=-2$

D. $x=-2;\,y=-1$

Lời giải
Chọn A

Ta có: $\left( 3x+2yi \right)+\left( 2+i \right)=2x-3i$
$\Leftrightarrow 3x+2+\left( 2y+1 \right)=2x-3i$

$ \Leftrightarrow \left\{ \begin{array}{l} 3x + 2 = 2x\\ 2y + 1 = – 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x = – 2\\ y = – 2 \end{array} \right..$

Câu 7.

(Đề Tham Khảo -2019) Tìm các số thực $a,b$ thỏa mãn $2a+(b+i)i=1+2i$ với $i$ là đơn vị ảo.

A. $a=0,b=1.$

B. $a=1,b=2.$

C. $a=0,b=2.$

D. $a=\frac{1}{2},b=1.$

Lời giải

Chọn B
$2a+(b+i)i=1+2i$ $\Leftrightarrow 2a+bi+{{i}^{2}}=1+2i$
$\Leftrightarrow (2a-1)+bi=1+2i$

$ \Leftrightarrow \left\{ \begin{array}{l} 2a – 1 = 1\\ b = 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 1\\ b = 2 \end{array} \right.$

Câu 8.

(Mã 103 2018) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 3x+yi \right)+\left( 4-2i \right)=5x+2i$ với $i$ là đơn vị ảo.

A. $x=2$; $y=4$

B. $x=-2$; $y=0$

C. $x=2$; $y=0$

D. $x=-2$; $y=4$

Lời giải

Chọn A
$\left( 3x+yi \right)+\left( 4-2i \right)=5x+2i$$\Leftrightarrow $$2x-4+\left( 4-y \right)i=0$$\Leftrightarrow $

$\left\{ \begin{align} 2x-4=0 \\ 4-y=0 \\ \end{align} \right.$$\Leftrightarrow $$\left\{ \begin{align} x=2 \\ y=4 \\ \end{align} \right.$.

Câu 9.

(Mã 102 – 2019) Cho số phức $z$ thoả mãn $3\left( \overline{z}-i \right)-\left( 2+3i \right)z=7-16i.$ Môđun của $z$ bằng

A. $3.$

B. $\sqrt{5}.$

C. $5.$

D. $\sqrt{3}.$

Lời giải

Chọn B
Đặt $z=a+bi\,\,\,\left( a;\,\,b\in \mathbb{R} \right)$.
Theo đề ta có
$3\left( a-bi-i \right)-\left( 2+3i \right)\left( a+bi \right)=7-16i$$\Leftrightarrow 3a-3bi-3i-2a-2bi-3ai+3b=7-16i$

$ \Leftrightarrow \left( {a + 3b} \right) + \left( { – 3a – 5b – 3} \right) = 7 – 16i$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a + 3b = 7}\\ { – 3a – 5b – 3 = – 16} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a + 3b = 7}\\ { – 3a – 5b = – 13} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a = 1}\\ {b = 2} \end{array}} \right.$

Vậy $\left| z \right|=\sqrt{{{1}^{2}}+{{2}^{2}}}=\sqrt{5}$.

Câu 10.

(Mã 101 – 2019) Cho số phức $z$ thỏa mãn $3\left( \overline{z}+i \right)-\left( 2-i \right)z=3+10i$. Môđun của $z$ bằng

A. $\sqrt{3}$.

B. $3$.

C. $5$.

D. $\sqrt{5}$.

Lời giải

Chọn D
Đặt $z=x+yi,\,\,\left( x,y\in \mathbb{R} \right)$

$3\left( {\bar z + i} \right) – \left( {2 – i} \right)z = 3 + 10i$

$ \Leftrightarrow 3\left( {x – yi + i} \right) – \left( {2 – i} \right)\left( {x + yi} \right) = 3 + 10i$

$ \Leftrightarrow x – y + \left( {x – 5y + 3} \right)i = 3 + 10i$

$ \Leftrightarrow \left\{ \begin{array}{l} x – y = 3\\ x – 5y + 3 = 10 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = 2\\ y = – 1 \end{array} \right.$

$z=2-i$

Vậy $\left| z \right|=\sqrt{5}$

Câu 11.

(THPT Cẩm Giàng 2 Năm 2019) Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 1-3i \right)=-1+6i$ với $i$ là đơn vị ảo.

A. $x=1$; $y=-3$.

B. $x=-1$; $y=-3$.

C. $x=-1$; $y=-1$.

D. $x=1$; $y=-1$.

Lời giải

Ta có: $\left( 2x-3yi \right)+\left( 1-3i \right)=-1+6i$$\Leftrightarrow 2x+1-\left( 3y+3 \right)i=-1+6i$.
Suy ra

$\left\{ \begin{array}{l} 2x + 1 = – 1\\ – 3y – 3 = 6 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = – 1\\ y = – 3 \end{array} \right..$

Câu 12.

Tìm hai số thực $x$ và $y$ thỏa mãn $\left( 2x-3yi \right)+\left( 3-i \right)=5x-4i$ với $i$ là đơn vị ảo.

A. $x=-1,y=-1$

B. $x=1,y=1$

C. $x=-1,y=1$

D. $x=1,y=-1$

Lời giải

Chọn B
Từ $\left( 2x-3yi \right)+\left( 3-i \right)=5x-4i\Leftrightarrow \left( 2x+3 \right)-\left( 3y+1 \right)i=5x-4i$

$ \Leftrightarrow \left\{ \begin{array}{l} 2x + 3 = 5\\ 3y + 1 = 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = 1\\ y = 1 \end{array} \right.$

Vậy $x=1,y=1$.

Câu 13.

(Chuyên Sơn La 2019) Tìm các số thực $x$ và $y$ thỏa mãn $\left( 3x-2 \right)+\left( 2y+1 \right)i=\left( x+1 \right)-\left( y-5 \right)i$, với $i$ là đơn vị ảo.

A. $x=\frac{3}{2},\,y=-2$.

B. $x=-\frac{3}{2},\,y=-\frac{4}{3}$.

C. $x=1,\,y=\frac{4}{3}$.

D. $x=\frac{3}{2},\,y=\frac{4}{3}$.

Lời giải

Ta có $\left( 3x-2 \right)+\left( 2y+1 \right)i=\left( x+1 \right)-\left( y-5 \right)i\Leftrightarrow \left( 3x-2 \right)+\left( 2y+1 \right)i=\left( x+1 \right)+\left( 5-y \right)i$

$ \Leftrightarrow \left\{ \begin{array}{l} 3x – 2 = x + 1\\ 2y + 1 = 5 – y \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = \frac{3}{2}\\ y = \frac{4}{3} \end{array} \right..$

Câu 14.

(Chuyên Phan Bội Châu 2019) Cho số phức $z=a+bi\ \left( a,b\in \mathbb{R} \right)$ thỏa mãn $\left( 1+i \right)z+2\overline{z}=3+2i$. Tính $P=a+b$

A. $P=1$

B. $P=-\frac{1}{2}$

C. $P=\frac{1}{2}$

D. $P=-1$

Lời giải

Ta có

$\left( {1 + i} \right)z + 2\bar z = 3 + 2i$ $ \Leftrightarrow \left( {1 + i} \right)\left( {a + bi} \right) + 2\left( {a – bi} \right) = 3 + 2i$ $ \Leftrightarrow 3a – b + \left( {a + b} \right)i = 3 + 2i$ $ \Leftrightarrow \left\{ \begin{array}{l} 3a – b = 3\\ a – b = 2 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = \frac{1}{2}\\ b = – \frac{3}{2} \end{array} \right.$

Vậy $P=a+b=-1$.

Câu 15.

(Chuyên KHTN -2019) Cho số phức $z$ thỏa mãn $\left( 2+3i \right)z+4-3i=13+4i$. Môđun của $z$ bằng

A. $2$.

B. $4$.

C. $2\sqrt{2}$.

D. $\sqrt{10}$.

Lời giải

$\left( {2 + 3i} \right)z + 4 – 3i = 13 + 4i$ $ \Leftrightarrow \left( {2 + 3i} \right)z = 9 + 7i$ $ \Leftrightarrow z = \frac{{9 + 7i}}{{2 + 3i}}$ $ \Leftrightarrow z = \frac{{\left( {9 + 7i} \right)\left( {2 – 3i} \right)}}{{4 + 9}}$ $ \Leftrightarrow z = \frac{{39 – 13i}}{{13}}$ $ \Leftrightarrow z = 3 – i$

Vậy $\left| z \right|=\sqrt{9+1}=\sqrt{10}$.

Câu 16.

(HSG Bắc Ninh 2019) Cho số phức $z=x+yi\,\,\left( x,y\in \mathbb{R} \right)$ thỏa mãn $\left( 1+2i \right)\overline{z}+z=3-4i$. Tính giá trị của biểu thức $S=3x-2y$.

A. $S=-12$

B. $S=-11$

C. $S=-13$

D. $S=-10$

Lời giải

$\left( {1 + 2i} \right)\bar z + z = 3 – 4i$ $ \Leftrightarrow \left\{ \begin{array}{l} 2x + 2y = 3\\ 2x = – 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = – 2\\ y = – \frac{7}{3} \end{array} \right.$

$ \Rightarrow S = – 13.$

Câu 17.

(Sở Bình Phước 2019) Tổng phần thực và phần ảo của số phức $z$ thoả mãn $iz+\left( 1-i \right)\bar{z}=-2i$ bằng

A. $6$

B. $-2$

C. $2$

D. $-6$

Lời giải

Chọn A
Giả sử số phức $z$ có dạng: $z=x+yi\,,\,x\,,\,y\in \mathbb{R}$.
Ta có:$iz+\left( 1-i \right)\bar{z}=-2i$$\Leftrightarrow i\left( x+yi \right)+\left( 1-i \right)\left( x-yi \right)=-2i$$\Leftrightarrow x-2y-yi=-2i$.

$ \Leftrightarrow \left\{ \begin{array}{l} x – 2y = 0\\ – y = – 2 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = 4\\ y = 2 \end{array} \right.$

$ \Rightarrow x + y = 6.$

Tổng phần thực và phần ảo của số phức $z$ bằng $6$.

Câu 18.

(Sở Bình Phước 2019) Cho $a,\,b\in \mathbb{R}$ và thỏa mãn $\left( a+bi \right)i-2a=1+3i$, với $i$ là đơn vị ảo. Giá trị $a-b$ bằng

A. $4$

B. $-10$

C. $-4$

D. $10$

Lời giải

Chọn D
Ta có

$\left( {a + bi} \right)i – 2a = 1 + 3i$ $ \Leftrightarrow – b – 2a + ai = 1 + 3i$ $ \Leftrightarrow \left\{ \begin{array}{l} – b – 2a = 1\\ a = 3 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = 3\\ b = – 7 \end{array} \right.$

Vậy $a-b=10$.

Câu 19.

(Chuyen Phan Bội Châu Nghệ An 2019) Cho số phức $z=a+bi\text{ (}a,b\in \mathbb{R}\text{)}$ thoả mãn $(1+i)z+2\overline{z}=3+2i$. Tính $P=a+b$

A. $P=1$.

B. $P=-\frac{1}{2}$.

C. $P=\frac{1}{2}$.

D. $P=-1$

Lời giải

$(1+i)z+2\overline{z}=3+2i\Leftrightarrow (1+i)(a+bi)+2(a-bi)=3+2i\Leftrightarrow (3a-b)+(a-b)i=3+2i$

$ \Leftrightarrow \left\{ \begin{array}{l} 3a – b = 3\\ a – b = 2 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = \frac{1}{2}\\ b = – \frac{3}{2} \end{array} \right..$

Suy ra: $P=a+b=-1$.

Câu 20.

(Chuyên Hạ Long -2019) Tìm số phức $z$ biết $4z+5\overline{z}=27-7i$.

A. $z=-3+7i$.

B. $z=-3-7i$.

C. $z=3-7i$.

D. $z=3+7i$.

Lời giải

Giả sử $z=a+bi\ \left( a,\ b\ \in R \right)$, khi đó $4(a+bi)+5(a-bi)=27-7i\Leftrightarrow 9a-bi=27-7i$

$ \Leftrightarrow \left\{ \begin{array}{l} 9a = 27\\ – b = – 7 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = 3\\ b = 7 \end{array} \right.$

$ \Rightarrow z = 3 + 7i.$

Câu 21.

(THPT Lê Quý Đôn Đà Nẵng 2019) Cho số phức $z$ thỏa mãn $\left( 3+2i \right)z+{{\left( 2-i \right)}^{2}}=4+i$. Mô đun của số phức $w=\left( z+1 \right)\overline{z}$ bằng.

A. $2$.

B. $\sqrt{10}$.

C. $\sqrt{5}$.

D. $4$.

Lời giải

$\left( {3 + 2i} \right)z + {\left( {2 – i} \right)^2} = 4 + i$ $ \Leftrightarrow \left( {3 + 2i} \right)z = 1 + 5i$ $ \Leftrightarrow z = 1 + i$

$w = \left( {z + 1} \right)\bar z = z\bar z + \bar z = \left( {1 + i} \right)\left( {1 – i} \right) + 1 – i = 2 + 1 – i = 3 – i$

$ \Rightarrow \left| w \right| = \sqrt {{3^2} + 1} = \sqrt {10} $

Câu 22.

(THPT Lê Quý Đôn Đà Nẵng 2019) Tìm các số thực $a,b$ thỏa mãn$\left( a-2b \right)+\left( a+b+4 \right)i=\left( 2a+b \right)+2bi$ với $i$ là đơn vị ảo.

A. $a=-3,\,b=1$.

B. $a=3,\,b=-1$.

C. $a=-3,\,b=-1$.

D. $a=3,\,b=1$.

Lời giải

Ta có: $\left( a-2b \right)+\left( a+b+4 \right)i=\left( 2a+b \right)+2bi$.

$ \Leftrightarrow \left\{ \begin{array}{l} a – 2b = 2a + b\\ a + b + 4 = 2b \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a + 3b = 0\\ a – b = – 4 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = – 3\\ b = 1 \end{array} \right.$

Câu 23.

Cho hai số phức ${{z}_{1}}=m+1-2i$ và ${{z}_{1}}=2-\left( m+1 \right)i$. Có bao nhiêu giá trị thực của tham số $m$ để ${{z}_{1}}.\,{{z}_{2}}-8+8i$ là một số thực.

A. $1$.

B. $2$.

C. $3$.

D. $4$.

Lời giải

Ta có: $z1.{\mkern 1mu} z2 – 8 + 8i = \left( {m + 1 – 2i} \right)\left[ {2 – \left( {m + 1} \right)i} \right] – 8 + 8i = – 8 + \left( { – {m^2} – 2m + 3} \right)i.$
Để ${{z}{1}}.\,{{z}{2}}-8+i$ là một số thực thì

$ – {m^2} – 2m + 3 = 0$ $ \Leftrightarrow \left[ \begin{array}{l} m = 1\\ m = – 3 \end{array} \right.$

Vậy có hai giá trị của tham số $m$ để ${{z}{1}}.\,{{z}{2}}-8+i$ là một số thực.

Câu 24.

(Chuyên Bắc Giang 2019) Tìm mô đun của số phức$z$biết $\left( 2z-1 \right)\left( 1+i \right)+\left( \overline{z}+1 \right)\left( 1-i \right)=2-2i$.

A. $\frac{1}{9}$

B. $\frac{\sqrt{2}}{3}$

C. $\frac{2}{9}$

D. $\frac{1}{3}$

Lời giải

Chọn B
Giả sử $z=a+bi\Rightarrow \overline{z}=a-bi$
Do đó $\left( 2z-1 \right)\left( 1+i \right)+\left( \overline{z}+1 \right)\left( 1-i \right)=2-2i$
$\Leftrightarrow \left( 2a+2bi-1 \right)\left( 1+i \right)+\left( a-bi+1 \right)\left( 1-i \right)=2-2i$
$\Leftrightarrow \left( 2a-2b-1 \right)+\left( 2a+2b-1 \right)i+\left( a-b+1 \right)-\left( a+b+1 \right)i=2-2i$

$ \Leftrightarrow \left\{ \begin{array}{l} \left( {2a – 2b – 1} \right) + \left( {a – b + 1} \right) = 2\\ \left( {2a + 2b – 1} \right) – \left( {a + b + 1} \right) = – 2 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} 3a – 3b = 2\\ a + b = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = \frac{1}{3}\\ b = – \frac{1}{3} \end{array} \right.$

Khi đó $\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}=\frac{\sqrt{2}}{3}$.

Câu 25.

Tính mô đun của số phức $z$ thỏa mãn $z\left( 1+2i \right)+\overline{z}\left( 1-i \right)+4-i=0$ với $i$ là đơn vị ảo.

A. $\sqrt{6}$.

B. $\sqrt{5}$.

C. $\sqrt{2}$.

D. $\sqrt{3}$.

Lời giải

Giả sử: $z=x+yi$, $x,y\in \mathbb{R}$.
Ta có: $z\left( 1+2i \right)+\overline{z}\left( 1-i \right)+4-i=0$$\Leftrightarrow $$\left( x+yi \right)\left( 1+2i \right)+\left( x-yi \right)\left( 1-i \right)+4-i=0$
$\Leftrightarrow $$\left( 2x-3y+4 \right)+\left( x-1 \right)i=0$$\Leftrightarrow $

$\left\{ \begin{array}{l} 2x – 3y + 4 = 0\\ x – 1 = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} y = 2\\ x = 1 \end{array} \right.$

$\Rightarrow z=1+2i\Rightarrow \left| z \right|=\sqrt{5}$.

Dạng 2. Tìm số phức thỏa mãn điều kiện cho trước

Câu 1.

Hỏi có bao nhiêu số phức z thỏa mãn đồng thời các điều kiện $\left| z-i \right|=5$ và ${{z}^{2}}$ là số thuần ảo?

A. $4$

B. $0$

C. $2$

D. $3$

Lời giải

Chọn A

Giả sử \[z=a+bi\Rightarrow {{z}^{2}}={{a}^{2}}-{{b}^{2}}+2abi\]

Vì $\left| z-i \right|=5$ và ${{z}^{2}}$ là số thuần ảo ta có hệ phương trình

$ \Rightarrow \left\{ \begin{array}{l} {a^2} + {(b – 1)^2} = 25\\ {a^2} – {b^2} = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} a = b\\ {b^2} + {(b – 1)^2} = 25 \end{array} \right.\\ \left\{ \begin{array}{l} a = – b\\ {b^2} + {(b – 1)^2} = 25 \end{array} \right. \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} a = b = 4\\ a = b = – 3\\ b = – a = 4\\ b = – a = – 3 \end{array} \right.$

Câu 2.

Cho số phức $z=a+bi\text{ }\left( a,\text{ }b\in \mathbb{R} \right)$ thoả mãn $z+2+i=\left| z \right|$. Tính $S=4a+b$.

A. $S=-4$

B. $S=2$

C. $S=-2$

D. $S=4$

Lời giải

Chọn A

$z + 2 + i = \left| z \right| \Leftrightarrow \left( {a + 2} \right) + \left( {b + 1} \right)i = \sqrt {{a^2} + {b^2}} $

$ \Leftrightarrow \left\{ \begin{array}{l} a + 2 = \sqrt {{a^2} + {b^2}} {\rm{ (1)}}\\ b + 1 = 0{\rm{ (2)}} \end{array} \right.$

Từ (2) ta có: $b=-1$. Thay vào (1):

$\sqrt {{a^2} + 1} = a + 2$ $ \Leftrightarrow \left\{ \begin{array}{l} a + 2 \ge 0\\ {a^2} + 1 = {(a + 2)^2} \end{array} \right.$ $ \Leftrightarrow a = \frac{{ – 3}}{4}$

Vậy $S=4a+b=-4$.

Câu 3.

Cho số phức $z=a+bi\,\,\left( a,b\in \mathbb{R} \right)$ thỏa mãn $z+2+i-\left| z \right|\left( 1+i \right)=0$ và $\left| z \right|>1$. Tính $P=a+b$.

A. $P=-1$

B. $P=-5$

C. $P=3$

D. $P=7$

Lời giải

Chọn D

Ta có: $z+2+i-\left| z \right|\left( 1+i \right)=0$$\Leftrightarrow a+bi+2+i-\sqrt{{{a}^{2}}+{{b}^{2}}}\left( 1+i \right)=0$

$ \Leftrightarrow a + 2 – \sqrt {{a^2} + {b^2}} + \left( {b + 1 – \sqrt {{a^2} + {b^2}} } \right)i = 0$

$ \Leftrightarrow \left\{ \begin{array}{l} a + 2 – \sqrt {{a^2} + {b^2}} = 0\,\,\left( 1 \right)\\ b + 1 – \sqrt {{a^2} + {b^2}} = 0\,\,\,\left( 2 \right) \end{array} \right.$

Lấy $\left( 1 \right)$ trừ $\left( 2 \right)$ ta được: $a-b+1=0\Leftrightarrow b=a+1$. Thế vào $\left( 1 \right)$ ta được:

$a + 2 – \sqrt {{a^2} + {{\left( {a + 1} \right)}^2}} = 0 \Leftrightarrow a + 2 = \sqrt {2{a^2} + 2a + 1} $

$ \Leftrightarrow \left\{ \begin{array}{l} a \ge – 2\\ {a^2} + 4a + 4 = 2{a^2} + 2a + 1 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a \ge – 2\\ {a^2} – 2a – 3 = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a \ge – 2\\ \left[ \begin{array}{l} a = 3\,\,\,\,\,\,\left( {tm} \right)\\ a = – 1\,\,\,\left( {tm} \right) \end{array} \right. \end{array} \right.$

Với $a=3\Rightarrow b=4$; $a=-1\Rightarrow b=0$.

Vì $\left| z \right| > 1 \Rightarrow z = 3 + 4i$

$ \Rightarrow \left\{ \begin{array}{l} a = 3\\ b = 4 \end{array} \right.$

$ \Rightarrow P = a + b = 3 + 4 = 7$

Câu 4.

Có bao nhiêu số phức $z$thỏa mãn $|z+2-i|=2\sqrt{2}$ và ${{\left( z-1 \right)}^{2}}$ là số thuần ảo?

A. $0$

B. $2$

C. $4$

D. $3$

Lời giải

Chọn D Gọi số phức $z=x+yi$ $\left( x,y\in \mathbb{R} \right)$, vì ${{\left( z-1 \right)}^{2}}=\left[ {{\left( x-1 \right)}^{2}}-{{y}^{2}} \right]+2\left( x-1 \right)yi$ là số thuần ảo nên theo đề bài ta có hệ phương trình:

$\left\{ \begin{array}{l} {\left( {x + 2} \right)^2} + {\left( {y – 1} \right)^2} = 8{\rm{ }} & (1)\\ {\left( {x – 1} \right)^2} = {y^2}{\rm{ }} & & (2) \end{array} \right.$

Từ $(2)$ suy ra: $y=\pm \text{ }(x-1)$

Với $y=x-1$, thay vào $(1)$, ta được: ${{\left( x+2 \right)}^{2}}+{{\left( x-2 \right)}^{2}}=8\Leftrightarrow {{x}^{2}}=0\Leftrightarrow x=0.$

Suy ra: $z=-i$.

Với $y=-(x-1)$, thay vào $(1)$, ta được:

${{\left( x+2 \right)}^{2}}+{{\left( -x \right)}^{2}}=8\Leftrightarrow 2{{x}^{2}}+4x-4=0\Leftrightarrow x=-1\pm \sqrt{3}.$

Suy ra: $z=\left( -1+\sqrt{3} \right)+\left( 2-\sqrt{3} \right)i$; $z=\left( -1-\sqrt{3} \right)+\left( 2+\sqrt{3} \right)i$

Vậy có 3 số phức thỏa mãn.

Câu 5.

Có bao nhiêu số phức $z$ thỏa mãn $\left| z \right|\left( z-5-i \right)+2i=\left( 6-i \right)z$?

A. $1$

B. $3$

C. $4$

D. $2$

Lời giải

Chọn B

Lây môđun hai vế của $\left( 1 \right)$ ta có:

$\sqrt{{{\left( \left| z \right|-6 \right)}^{2}}+1}.\left| z \right|$$=\sqrt{25{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}}$

Bình phương và rút gọn ta được: ${{\left| z \right|}^{4}}-12{{\left| z \right|}^{3}}+11{{\left| z \right|}^{2}}+4\left| z \right|-4=0$$\Leftrightarrow \left( \left| z \right|-1 \right)\left( {{\left| z \right|}^{3}}-11{{\left| z \right|}^{2}}+4 \right)=0$

$ \Leftrightarrow \left[ \begin{array}{l} \left| z \right| = 1\\ {\left| z \right|^3} – 11{\left| z \right|^2} + 4 = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} \left| z \right| = 1\\ \left| z \right| = 10,9667…\\ \left| z \right| = 0,62…\\ \left| z \right| = – 0,587… \end{array} \right.$

Câu 6.

Có bao nhiêu số phức thỏa mãn $\left| z \right|\left( z-6-i \right)+2i=\left( 7-i \right)z$?

A. $1$

B. $4$

C. $2$

D. $3$

Lời giải

Chọn D

Đặt $\left| z \right|=a\ge 0,a\in \mathbb{R}$, khi đó ta có

$\left| z \right|\left( z-6-i \right)+2i=\left( 7-i \right)z$$\Leftrightarrow a\left( z-6-i \right)+2i=\left( 7-i \right)z$$\Leftrightarrow \left( a-7+i \right)z=6a+ai-2i$$\Leftrightarrow \left( a-7+i \right)z=6a+\left( a-2 \right)i$$\Leftrightarrow \left| \left( a-7+i \right) \right|\left| z \right|=\left| 6a+\left( a-2 \right)i \right|$ $\Leftrightarrow \left[ {{\left( a-7 \right)}^{2}}+1 \right]{{a}^{2}}=36{{a}^{2}}+{{\left( a-2 \right)}^{2}}$$\Leftrightarrow {{a}^{4}}-14{{a}^{3}}+13{{a}^{2}}+4a-4=0$

$ \Leftrightarrow \left( {a – 1} \right)\left( {{a^3} – 13{a^2} + 4} \right) = 0$

$ \Leftrightarrow \left[ \begin{array}{l} a = 1\\ {a^3} – 12{a^2} + 4 = 0 \end{array} \right.$

Xét hàm số $f\left( a \right)={{a}^{3}}-13{{a}^{2}}\left( a\ge 0 \right)$, có bảng biến thiên là

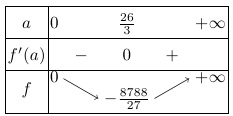
Đường thẳng $y=-4$ cắt đồ thị hàm số $f\left( a \right)$ tại hai điểm nên phương trình ${{a}^{3}}-12{{a}^{2}}+4=0$ có hai nghiệm khác $1$ (do $f\left( 1 \right)\ne 0$). Mỗi giá trị của $a$ cho ta một số phức $z$.

Vậy có $3$ số phức thỏa mãn điều kiện.

Câu 7.

Có bao nhiêu số phức $z$ thỏa mãn $\left| z \right|\left( z-3-i \right)+2i=\left( 4-i \right)z$?

A. $1$

B. $3$

C. $2$

D. $4$

Lời giải

Chọn B

$\Rightarrow \sqrt{{{\left( \left| z \right|-4 \right)}^{2}}+1}.\left| z \right|=\sqrt{9{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}}$ (1). Đặt $m=\left| z \right|\ge 0$ ta có $\left( 1 \right)\Leftrightarrow \left( {{\left( m-4 \right)}^{2}}+1 \right).{{m}^{2}}=9{{m}^{2}}+{{\left( m-2 \right)}^{2}}$$\Leftrightarrow {{m}^{4}}-8{{m}^{3}}+7{{m}^{2}}+4m-4=0$

$ \Leftrightarrow \left( {m – 1} \right)\left( {{m^3} – 7{m^2} + 4} \right) = 0$

$ \Leftrightarrow \left[ \begin{array}{l} m = 1\\ {m^3} – 7{m^2} + 4 = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} m = 1\\ m \approx 6,91638\\ m \approx 0.80344\\ m \approx – 0.71982 & \left( {\rm{L}} \right) \end{array} \right.$

Từ (*) ta suy ra ứng với mỗi $\left| z \right|=m$ sẽ có một số phức $z=\frac{3m+\left( m-2 \right)i}{m-4+i}$ thỏa mãn đề bài.

Vậy có $3$ số phức $z$ thỏa mãn yêu cầu bài toán.

Câu 8.

A. $\left| z \right|=17$

B. $\left| z \right|=\sqrt{17}$

C. $\left| z \right|=\sqrt{10}$

D. $\left| z \right|=10$

Lời giải

Chọn C

Đặt $z=x+yi;x,y\in \mathbb{R}$. Theo bài ra ta có:

$\left\{ \begin{array}{l} {\left( {x + 3} \right)^2} + {y^2} = 25\\ {x^2} + {\left( {y – 2} \right)^2} = {\left( {x – 2} \right)^2} + {\left( {y – 2} \right)^2} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {\left( {x + 3} \right)^2} + {y^2} = 25\\ – 4x + 4 = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} {y^2} = 9\\ x = 1 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} y = \pm 3\\ x = 1 \end{array} \right.$

Vậy $\left| z \right|=\sqrt{10}$

Câu 9.

Có bao nhiêu số phức $z$ thỏa mãn $\left| z+3i \right|=\sqrt{13}$ và $\frac{z}{z+2}$ là số thuần ảo?

A. $0$

B. $2$

C. Vô số

D. $1$

Lời giải

Chọn B

Gọi số phức $z=a+bi,\left( a,b\in \mathbb{R} \right)$

Ta có $\left| z+3i \right|=\sqrt{13}\Leftrightarrow \left| a+bi+3i \right|=\sqrt{13}$$\Leftrightarrow {{a}^{2}}+{{\left( b+3 \right)}^{2}}=13$

$\Leftrightarrow {{a}^{2}}+{{b}^{2}}+6b-4=0\Leftrightarrow {{a}^{2}}+{{b}^{2}}=4-6b\left( 1 \right)$

$\frac{z}{z+2}=1-\frac{2}{z+2}=1-\frac{2}{a+2+bi}=1-\frac{2\left( a+2-bi \right)}{{{\left( a+2 \right)}^{2}}+{{b}^{2}}}$.

$=\frac{{{\left( a+2 \right)}^{2}}+{{b}^{2}}-2a-4}{{{\left( a+2 \right)}^{2}}+{{b}^{2}}}+\frac{2b}{{{\left( a+2 \right)}^{2}}+{{b}^{2}}}i$$=\frac{{{a}^{2}}+{{b}^{2}}+2a}{{{\left( a+2 \right)}^{2}}+{{b}^{2}}}+\frac{2b}{{{\left( a+2 \right)}^{2}}+{{b}^{2}}}i$ Do $\frac{z}{z+2}$ là số thuần ảo nên:

$\frac{{{a^2} + {b^2} + 2a}}{{{{\left( {a + 2} \right)}^2} + {b^2}}} = 0$ $ \Leftrightarrow \left\{ \begin{array}{l} {a^2} + {b^2} + 2a = 0\,\left( 2 \right)\\ a \ne – 2\\ b \ne 0 \end{array} \right.$

Thay $\left( 1 \right)$ vào $\left( 2 \right)$ ta có $4-6b+2a=0\Leftrightarrow a=3b-2$ thay vào $\left( 1 \right)$ ta có ${{\left( 3b-2 \right)}^{2}}+{{b}^{2}}-4+6b=0\Leftrightarrow 10{{b}^{2}}-6b=0$

$ \Leftrightarrow \left[ \begin{array}{l} b = 0(L)\\ b = \frac{3}{5} \Rightarrow a = \frac{{ – 1}}{5} \end{array} \right.$

Vậy có 1 số phức cần tìm.

Câu 10.

Có bao nhiêu số phức $z$ thỏa mãn điều kiện $\left| z.\overline{z}+z \right|=2$ và $\left| z \right|=2$?

A. $2$.

B. $3$.

C. $1$.

D. $4$.

Lời giải

Đặt $z=x+yi$ ($x$; $y\in \mathbb{R}$; ${{i}^{2}}=-1$). Theo bài ra ta có:

$\left\{ {\begin{array}{*{20}{c}} {\left| {{x^2} + {y^2} + x + yi} \right| = 2}\\ {\sqrt {{x^2} + {y^2}} = 2} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {\left| {4 + x + yi} \right| = 2}\\ {{x^2} + {y^2} = 4\,\,\,\,\,} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{{\left( {4 + x} \right)}^2} + {y^2} = 4}\\ {{x^2} + {y^2} = 4\,\,\,\,\,\,\,\,} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x = – 2}\\ {y = 0} \end{array}} \right.$

Dạng 3. Một số bài toán liên quan đến số phức có lũy thừa bậc cao, chứa tham số

Câu 1.

Vậy có $1$ số phức thỏa yêu cầu bài toán là $z=-2$.

Cho số phức $z={{\left( 1+i \right)}^{2019}}$. Phần thực của $z$ bằng

A. $-{{2}^{1009}}$.

B. ${{2}^{2019}}$.

C. $-{{2}^{2019}}$.

D. ${{2}^{1009}}$.

Lời giải

Cách 1: Phương pháp lượng giác

Xét số phức ${{z}_{1}}=1+i=\sqrt{2}\left( \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i \right)=\sqrt{2}\left( cos\frac{\pi }{4}+i\sin \frac{\pi }{4} \right)$

Ta có số phức $z={{z}_{1}}^{2019}={{\left( 1+i \right)}^{2019}}={{\sqrt{2}}^{2019}}\left( cos\frac{2019\pi }{4}+i\sin \frac{2019\pi }{4} \right)$

$={{\sqrt{2}}^{2019}}\left( cos\frac{3\pi }{4}+i\sin \frac{3\pi }{4} \right)={{\sqrt{2}}^{2019}}\left( -\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i \right)=-{{2}^{1009}}+{{2}^{1009}}i$

Phần thực của $z$ bằng $-{{2}^{1009}}$.

Cách 2:

Ta có $z={{\left( 1+i \right)}^{2019}}=\frac{{{(1+i)}^{2020}}}{1+i}=\frac{{{(-4)}^{505}}}{(1+i)}={{(-4)}^{505}}(\frac{1}{2}-\frac{1}{2}i)=-{{2}^{1009}}+{{2}^{1009}}i$

Phần thực của $z$ bằng $-{{2}^{1009}}$.

Câu 2.

Số phức $z=\left( 1+i \right)+{{\left( 1+i \right)}^{2}}+…+{{\left( 1+i \right)}^{2018}}$ có phần ảo bằng

A. ${{2}^{1009}}+1$.

B. $1-{{2}^{1009}}$.

C. ${{2}^{1009}}-1$.

D. $-\left( {{2}^{1009}}+1 \right)$.

Lời giải

$z=\left( 1+i \right)+{{\left( 1+i \right)}^{2}}+…+{{\left( 1+i \right)}^{2018}}$

$=\left( 1+i \right)\frac{{{\left( 1+i \right)}^{2018}}-1}{\left( 1+i \right)-1}=\left( 1+i \right)\frac{{{2}^{1009}}i-1}{i}$

$=\left( 1+i \right)\left( {{2}^{1009}}+i \right)={{2}^{1009}}-1+\left( {{2}^{1009}}+1 \right)i$.

$\Rightarrow z$ có phần ảo bằng ${{2}^{1009}}+1$.

Câu 3.

Gọi $T$ là tổng phần thực, phần ảo của số phức $w=i+2{{i}^{2}}+3{{i}^{3}}+…+2018{{i}^{2018}}$. Tính giá trị của T.

A. $T=0.$

B. $T=-1.$

C. $T=2.$

D. $T=-2.$

Lời giải

$w=i\left( 1+2i+3{{i}^{2}}+…+2018{{i}^{2017}} \right)$

Xét $f(x)=x+{{x}^{2}}+{{x}^{3}}+…+{{x}^{2018}}=x\frac{{{x}^{2018}}-1}{x-1}=\frac{{{x}^{2019}}-x}{x-1}$

$f'(x)=1+2x+3{{x}^{2}}+…+2018{{x}^{2017}}=\frac{\left( 2019{{x}^{2018}}-1 \right)(x-1)-\left( {{x}^{2019}}-x \right)}{{{(x-1)}^{2}}}$

$w=i\left( 1+2i+3{{i}^{2}}+…+2018{{i}^{2017}} \right)=i.f(i)=i\frac{\left( 2019{{i}^{2018}}-1 \right)(i-1)-\left( {{i}^{2019}}-i \right)}{{{(i-1)}^{2}}}$

$=i\frac{-2020(i-1)+2i}{-2i}=-1010+1009i$

$T=-1010+1009=-1$.

Câu 4.

Cho số phức $z$ thỏa mãn ${{z}^{2}}+z+1=0$. Tính giá trị biểu thức

$P={{\left( z+\frac{1}{z} \right)}^{2}}+{{\left( {{z}^{2}}+\frac{1}{{{z}^{2}}} \right)}^{2}}+…+{{\left( {{z}^{2019}}+\frac{1}{{{z}^{2019}}} \right)}^{2}}$.

A. $P=4038$.

B. $P=2019$.

C. $P=673$.

D. $P=6073$.

Lời giải

Chọn A Ta có ${{z}^{2}}+z+1=0$ $\Rightarrow \left( z-1 \right)\left( {{z}^{2}}+z+1 \right)=0$ $\Rightarrow {{z}^{3}}=1$

$ \Rightarrow \left\{ \begin{array}{l} {z^{3n}} = 1\\ {z^{3n + 1}} = z\\ {z^{3n + 2}} = {z^2} \end{array} \right.$

Mà $P=\sum\limits_{k=1}^{2019}{{{\left( {{z}^{k}}+\frac{1}{{{z}^{k}}} \right)}^{2}}}=\sum\limits_{k=1}^{2019}{\left( {{z}^{2k}}+\frac{1}{{{z}^{2k}}}+2 \right)=}\sum\limits_{k=1}^{2019}{\left( {{z}^{2k}}+\frac{1}{{{z}^{2k}}} \right)+2.2019}$

Ta có ${{z}^{2}}+z+1={{z}^{2}}+{{z}^{4}}+{{z}^{6}}=…={{z}^{4034}}+{{z}^{4036}}+{{z}^{4038}}=0$,

$\frac{1}{{{z}^{2}}}+\frac{1}{{{z}^{4}}}+\frac{1}{{{z}^{6}}}=\frac{{{z}^{2}}+{{z}^{4}}+{{z}^{6}}}{{{z}^{6}}}=\frac{{{z}^{2}}+z+1}{{{z}^{6}}}=0$

Tương tự $\frac{1}{{{z}^{8}}}+\frac{1}{{{z}^{10}}}+\frac{1}{{{z}^{12}}}=…=\frac{1}{{{z}^{4034}}}+\frac{1}{{{z}^{4036}}}+\frac{1}{{{z}^{4038}}}=0$

Vậy $P=4038$.

Câu 5.

Khai triển của biểu thức ${{\left( {{x}^{2}}+x+1 \right)}^{2018}}$ được viết thành ${{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+…+{{a}_{4036}}{{x}^{4036}}$. Tổng $S={{a}_{0}}-{{a}_{2}}+{{a}_{4}}-{{a}_{6}}+…-{{a}_{4034}}+{{a}_{4036}}$ bằng

A. ${{2}^{1009}}$.

B. $-{{2}^{1009}}$.

C. $0$.

D. $-1$.

Lời giải

${{\left( {{x}^{2}}+x+1 \right)}^{2018}}$$={{a}_{0}}+{{a}_{1}}x+{{a}_{2}}{{x}^{2}}+…+{{a}_{4036}}{{x}^{4036}}$.

Thay $x=i$ với ${{i}^{2}}=-1$ ta được:

${{\left( -1 \right)}^{1009}}={{a}_{0}}+{{a}_{1}}i+{{a}_{2}}{{i}^{2}}+{{a}_{3}}{{i}^{3}}+…+{{a}_{4034}}{{i}^{4034}}+{{a}_{4035}}{{i}^{4035}}+{{a}_{4036}}{{i}^{4036}}$.

Đối chiếu phần thực ở hai vế ta được: $-1={{a}_{0}}-{{a}_{2}}+{{a}_{4}}-{{a}_{6}}+…-{{a}_{4034}}+{{a}_{4036}}$.

Câu 6.

Gọi $S$ là tập hợp tất cả các giá trị thực của tham số $m$ để tồn tại duy nhất số phức $z$ thỏa mãn $z.\overline{z}=1$ và $\left| z-\sqrt{3}+i \right|=m$. Tìm số phần tử của $S$.

A. $2$.

B. $4$.

C. $1$.

D. $3$.

Lời giải

Chọn A

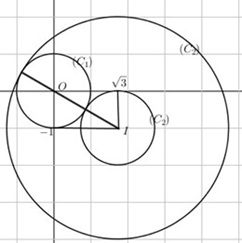
Gọi $z=x+yi\,,\,(x,y\in \mathbb{R})$, ta có hệ:

$\left\{ \begin{array}{l} {x^2} + {y^2} = 1{\rm{ }}(1)\\ {\left( {x – \sqrt 3 } \right)^2} + {\left( {y + 1} \right)^2} = {m^2}{\rm{ }}(m \ge 0) \end{array} \right.$

Ta thấy $m=0\Rightarrow z=\sqrt{3}-i$ không thỏa mãn $z.\overline{z}=1$ suy ra $m>0$.

Xét trong hệ tọa độ $Oxy$ tập hợp các điểm thỏa mãn $\left( 1 \right)$ là đường tròn $({{C}_{1}})$ có $O(0;0),{{R}_{1}}=1$, tập hợp các điểm thỏa mãn $\left( 2 \right)$ là đường tròn $({{C}_{2}})$ tâm $I\left( \sqrt{3};-1 \right),{{R}_{2}}=m$, ta thấy $OI=2>{{R}_{1}}$ suy ra $I$ nằm ngoài $({{C}_{1}})$.

Để có duy nhất số phức $z$ thì hệ có nghiệm duy nhất khi đó tương đương với $({{C}_{1}}),({{C}_{2}})$ tiếp xúc ngoài hoặc tiếp xúc trong, điều này xảy ra khi $OI={{R}_{1}}+{{R}_{2}}\Leftrightarrow m+1=2\Leftrightarrow m=1$ hoặc ${{R}_{2}}={{R}_{1}}+OI\Leftrightarrow m=1+2=3$.

Dạng 4. Tìm Min, Max mođun của số phức.

Câu 1.

Xét hai số phức ${{z}_{1}},\,{{z}_{2}}$ thỏa mãn $\left| {{z}_{1}} \right|=1,\left| {{z}_{2}} \right|=2$ và $\left| {{z}_{1}}-{{z}_{2}} \right|=\sqrt{3}$. Giá trị lớn nhất của $\left| 3{{z}_{1}}+{{z}_{2}}-5i \right|$ bằng

A. $5-\sqrt{19}.$

B. $5+\sqrt{19}.$

C. $-5+2\sqrt{19}.$

D. $5+2\sqrt{19}.$

Lời giải

Chọn B

Đặt ${{z}_{1}}=a+bi,{{z}_{2}}=c+di$ với $a,b,c,d\in \mathbb{R}.$ Theo giả thiết thì

${{a}^{2}}+{{b}^{2}}=1,\text{ }{{c}^{2}}+{{d}^{2}}=4,\text{ }{{(a-c)}^{2}}+{{(b-d)}^{2}}=3.$

Do đó ${{a}^{2}}-2ac+{{c}^{2}}+{{b}^{2}}-2bd+{{d}^{2}}=3\Rightarrow ac+bd=1.$

Ta có $3{{z}_{1}}+{{z}_{2}}=3(a+c)+(3b+d)i$ nên

$\left| 3{{z}_{1}}+{{z}_{2}} \right|={{(3a+c)}^{2}}+{{(3b+d)}^{2}}=9({{a}^{2}}+{{b}^{2}})+({{c}^{2}}+{{d}^{2}})+6(ac+bd)=19.$

Áp dụng bất đẳng thức $\left| z+{z}’ \right|\le \left| z \right|+\left| {{z}’} \right|$, ta có ngay

$\left| 3{{z}_{1}}+{{z}_{2}}-5i \right|\le \left| 3{{z}_{1}}+{{z}_{2}} \right|+\left| -5i \right|=\sqrt{19}+5.$

Câu 2.

A. $\sqrt{13}+1$.

B. $\sqrt{10}+1$.

C. $\sqrt{13}$.

D. $\sqrt{10}$.

Lời giải

Chọn C

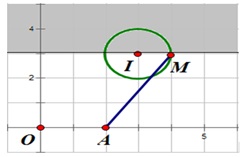
Gọi $M\left( x;y \right)$ là điểm biểu diễn số phức $z$ ta có:

$\left| {z – 2i} \right| \le \left| {z – 4i} \right|$

$ \Leftrightarrow {x^2} + {\left( {y – 2} \right)^2} \le {x^2} + {\left( {y – 4} \right)^2}$

$ \Leftrightarrow y \le 3;$

$\left| {z – 3 – 3i} \right| = 1$

$ \Leftrightarrow $ điểm M nằm trên đường tròn tâm $I\left( 3;3 \right)$ và bán kính bằng 1.

Biểu thức $P=\left| z-2 \right|=AM$ trong đó $A\left( 2;0 \right)$, theo hình vẽ thì giá trị lớn nhất của $P=\left| z-2 \right|$ đạt được khi $M\left( 4;3 \right)$ nên $\max P=\sqrt{{{\left( 4-2 \right)}^{2}}+{{\left( 3-0 \right)}^{2}}}=\sqrt{13}$.

Câu 4.

A. $3\sqrt{3}$.

B. $2\sqrt{3}$.

C. $5\sqrt{2}$.

D. $5\sqrt{3}$.

Lời giải

Chọn D

Ta có

$z-w=3+4i\Rightarrow {{\left| z-w \right|}^{2}}={{\left| 3+4i \right|}^{2}}=25$.

$\Rightarrow {{\left| z \right|}^{2}}+{{\left| w \right|}^{2}}-\left( z.\overline{w}+\overline{z}.w \right)=25$.

$\left| z+2w \right|=10\Leftrightarrow {{\left| z+2w \right|}^{2}}=100$,$\left( 1 \right)$.

$\Rightarrow {{\left| z \right|}^{2}}+4{{\left| w \right|}^{2}}-2\left( z.\overline{w}+\overline{z}.w \right)=100$,$\left( 2 \right)$.

Từ $\left( 1 \right)$ và $\left( 2 \right)$ $\Rightarrow 3{{\left| z \right|}^{2}}+6{{\left| w \right|}^{2}}=150$.

$P=\left| z \right|+\left| w \right|\le \sqrt{\left( \frac{1}{3}+\frac{1}{6} \right)\left( 2{{\left| z \right|}^{2}}+6{{\left| w \right|}^{2}} \right)}=5\sqrt{3}$.

Câu 5.

A. $\max T=\sqrt{176}$.

B. $\max T=14$.

C. $\max T=4$.

D. $\max T=\sqrt{106}$.

Lời giải

Chọn D

Đặt $z=x+yi\left( x,y\in \mathbb{R} \right)$. Do $z+w=3+4i$ nên $ w=\left( 3-x \right)+\left( 4-y \right)i$.

Mặt khác $\left| z-w \right|=9$ nên $\left| z-w \right|=\sqrt{{{\left( 2x-3 \right)}^{2}}+{{\left( 2y-4 \right)}^{2}}}=\sqrt{4{{x}^{2}}+4{{y}^{2}}-12x-16y+25}=9$

$\Leftrightarrow $$2{{x}^{2}}+2{{y}^{2}}-6x-8y=28$$\left( 1 \right)$.

Suy ra $T=\left| z \right|+\left| w \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}+\sqrt{{{\left( 3-x \right)}^{2}}+{{\left( 4-y \right)}^{2}}}$.

Áp dụng bất đẳng thức Bunyakovsky ta có ${{T}^{2}}\le 2\left( 2{{x}^{2}}+2{{y}^{2}}-6x-8y+25 \right) $$\left( 2 \right)$.

Dấu ”=” xảy ra khi $ \sqrt{{{x}^{2}}+{{y}^{2}}}=\sqrt{{{\left( 3-x \right)}^{2}}+{{\left( 4-y \right)}^{2}}}$.

Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có:

${T^2} \le 2.\left( {28 + 25} \right)$

$ \Leftrightarrow – \sqrt {106} \le T \le \sqrt {106} $

Vậy $MaxT=\sqrt{106}$.

————————————-

Chúc các em có những kỳ thi thành công rực rỡ!

Đề xuất cho bạn

Chuyên mục: Bài viết mớiChủ đề giải tích 12

0 Bình luận

Trả lời Hủy

Bạn phải đăng nhập để bình luận.

error: Content is protected !!

SỐ PHỨC

Đăng bởi ADMIN vào 23/03/202223/03/2022

SỐ PHỨC

I. KIẾN THỨC CẦN NHỚ:

1. Định nghĩa số phức

· Chú ý:

2. Hai số phức bằng nhau, đối nhau

3. Số phức liên hợp.

4. Biểu diễn hình học.

5. Mô đun của số phức.

6. Các phép toán trên tập số phức.

7. Lũy thừa của đơn vị ảo

8. Căn bậc 2 của số thực âm.

9. Giải phương trình bậc 2 trên tập số phức.

II. PHÂN DẠNG BÀI TẬP

III. Ví dụ minh họa

Ví dụ 1.

Ví dụ 2.

Ví dụ 3.

Ví dụ 4.

Ví dụ 5.

Dạng 1. Tìm số phức

Hướng dẫn và lời giải

Câu 1.

Lời giảiChọn D

Câu 2.

Câu 3.

Lời giảiChọn C

Câu 4.

Lời giảiChọn A

Câu 5.

Lời giảiChọn A

Câu 6.

Lời giảiChọn A

Câu 7.

Lời giải

Câu 8.

Lời giải

Câu 9.

Lời giải

Câu 10.

Lời giải

Câu 11.

Lời giải

Câu 12.

Lời giải

Câu 13.

Lời giải

Câu 14.

Lời giải

Câu 15.

Lời giải

Câu 16.

Lời giải

Câu 17.

Lời giải

Câu 18.

Lời giải

Câu 19.

Lời giải

Câu 20.

Lời giải

Câu 21.

Lời giải

Câu 22.

Lời giải

Câu 23.

Lời giải

Câu 24.

Lời giải

Câu 25.

Lời giải

Dạng 2. Tìm số phức thỏa mãn điều kiện cho trước

Câu 1.

Lời giải

Câu 2.

Lời giải

Câu 3.

Lời giải

Câu 4.

Lời giải
Chọn D

Lời giải
Chọn C

Lời giải
Chọn A

Lời giải
Chọn A

Lời giải
Chọn A