TÍCH MỘT VÉC TƠ VỚI MỘT SỐ

BÀI 3:  TÍCH MỘT SỐ VỚI MỘT VÉC TƠ

I – LÝ THUYẾT

1. Định nghĩa

Cho vectơ $\vec{a}$ và một số $k \in R$. Tích $k.\vec a$ là một vectơ
được xác định như sau:    
+ $k\vec{a}$ cùng hướng với $\vec{a}$ nếu k > 0,    
+ $k\vec{a}$ ngược hướng với $\vec{a}$ nếu k<0.
+ $\left| k\vec{a} \right|=\left| k \right|.\left| {\vec{a}} \right|$.

2. Tính chất

+ $(k + l)\vec a = k\vec a + l\vec a$
+ $k\left( {l\vec a} \right) = (kl)\vec a$
+ $0\vec a = \vec 0$
+ $k.\overrightarrow 0 = \overrightarrow 0 $

3. Điều kiện để hai vectơ cùng phương

$\vec a;\vec b$ cùng phương khi và chỉ khi $\exists k \in R;\vec b = k\vec a$ với $\left( {\vec a \ne \vec 0} \right)$.

4. Điều kiện ba điểm thẳng hàng

A, B, C thẳng hàng khi và chỉ khi tồn tại một số $k \ne 0$ sao cho: $\overrightarrow {AB} = k\overrightarrow {AC} $

5. Biểu thị một vectơ theo hai vectơ không cùng phương

Cho hai vectơ không cùng phương: ${\vec a}$ , ${\vec b}$ và ${\vec x}$ tuỳ ý.
Khi đó tồn tại duy nhất cặp số (m;n) sao cho : $\vec x = m\vec a + n\vec b$

6. Chú ý

* Hệ thức trung điểm đoạn thẳng

Gọi M là trung điểm AB. Ta luôn có:

+ $\overrightarrow{MA}+\overrightarrow{MB}=\vec{0}$
+  $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OM}$ với (O tuỳ ý).

*Hệ thức trọng tâm tam giác    

G là trọng tâm tam giác ABC khi:

+  $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$                                   
+ $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$ (O tuỳ ý)..

II – DẠNG TOÁN

Dạng 1: Xác định vectơ  $k\overrightarrow{a}$  

Phương pháp: Để chứng minh một đẳng thức vectơ hoặc phân tích một vectơ theo hai vectơ không cùng phương, ta thường sử dụng:

– Qui tắc ba điểm để phân tích các vectơ.

– Các hệ thức thường dùng như: hệ thức trung điểm, hệ thức trọng tâm tam giác.

– Tính chất của các hình.

Ví dụ 1: Cho $\overrightarrow{a}=\overrightarrow{AB}$ và điểm O. Xác định hai điểm M và N sao cho: $\overrightarrow{OM}=3\overrightarrow{a};\,\,\,\overrightarrow{ON}=-4\overrightarrow{a}$

Hướng dẫn giải:

 Vẽ d đi qua O và // với giá của $\overrightarrow{a}$ (nếu O nằm trên giá của $\overrightarrow{a}$ thì d là giá của $\overrightarrow{a}$)

– Trên d lấy điểm M sao cho OM=3| $\overrightarrow{a}$|, $\overrightarrow {OM} $ và $\overrightarrow{a}$ cùng hướng khi đó $\overrightarrow{OM}=3\overrightarrow{a}$.

– Trên d lấy điểm N sao cho ON= 4|$\overrightarrow{a}$|, $\overrightarrow{ON}$ và $\overrightarrow{a}$ ngược hướng nên $\overrightarrow{ON}=-4\overrightarrow{a}$

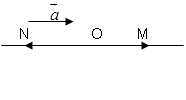
Ví dụ 2: Cho đoạn thẳng AB và M là một điểm nằm trên đoạn AB sao cho AM=$\frac{1}{5}$AB. Tìm k trong các đẳng thức sau:

$a)\overrightarrow{AM}=k\overrightarrow{AB};\,\,\,\,\,\,\,\,\,b)\,\overrightarrow{MA}=k\overrightarrow{MB};\,\,\,\,\,\,\,\,\,\,\,\,c)\,\overrightarrow{MA}=k\overrightarrow{AB}$

Hướng dẫn giải:

a) $\overrightarrow{AM}=k\overrightarrow{AB}\Rightarrow |k|=\frac{|\overrightarrow{AM}|}{|\overrightarrow{AB}|}=\frac{AM}{AB}=\frac{1}{5}$, vì $\overrightarrow{AM}\uparrow \uparrow \overrightarrow{AB}$=> k= $\frac{1}{5}$

b) k= -$\frac{1}{4}$           

c) k= -$\frac{1}{5}$

Ví dụ 3: a) Chứng minh:vectơ đối của $5\overrightarrow{a}$  là $\left( -5 \right)\overrightarrow{a}$

              b) Tìm vectơ đối của các véctơ $2\overrightarrow{a}+3\overrightarrow{b}$, $\overrightarrow{a}-2\overrightarrow{b}$

Hướng dẫn giải:

a) $-5\overrightarrow{a}=\left( -1 \right)\left( 5\overrightarrow{a} \right)=\left( \left( -1 \right).5 \right)\overrightarrow{a}=\left( -5 \right)\overrightarrow{a}$

b) $-\left( 2\overrightarrow{a}+3\overrightarrow{b} \right)=\left( -1 \right)\left( 2\overrightarrow{a}+3\overrightarrow{b} \right)=\left( -1 \right)2\overrightarrow{a}+\left( -1 \right)3\overrightarrow{b}=\left( -2 \right)\overrightarrow{a}+\left( -3 \right)\overrightarrow{b}=-2\overrightarrow{a}-3\overrightarrow{b}$

Dạng 2: Phân tích một vec tơ theo hai vectơ không cùng phương

Ví dụ 4: Cho DABC có trọng tâm G. Cho các điểm D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB và I là giao điểm của AD và EF. Đặt $\overrightarrow{u}=\overrightarrow{AE};\,\,\overrightarrow{v}=\overrightarrow{AF}$. Hãy phân tích các vectơ $\overrightarrow{AI},\,\overrightarrow{AG},\,\overrightarrow{DE},\,\overrightarrow{DC}$ theo hai vectơ $\overrightarrow{u},\overrightarrow{v}$.

Hướng dẫn giải:

Ta có $\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AE}+\overrightarrow{AF})=\frac{1}{2}\overrightarrow{u}+\frac{1}{2}\overrightarrow{v}$

$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}=\frac{2}{3}\overrightarrow{u}+\frac{2}{3}\overrightarrow{v}$

            $\overrightarrow{DE}=\overrightarrow{FA}=-\overrightarrow{AF}=0.\overrightarrow{u}+(-1)\overrightarrow{v}$

            $\overrightarrow{DC}=\overrightarrow{FE}=\overrightarrow{AE}-\overrightarrow{AF}=\overrightarrow{u}-\overrightarrow{v}$

Ví dụ 5: Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB= 2MC. Hãy phân tích vectơ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{u}=\overrightarrow{AB,}\,\,\,\overrightarrow{v}=\overrightarrow{AC}$.

Hướng dẫn giải:

            Ta có $\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$

            mà $\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$

            => $\overrightarrow{AM}=\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{3}\overrightarrow{u}+\frac{2}{3}\overrightarrow{v}$

Dạng 3: Chứng minh 3 điểm thẳng hàng

+ A, B, C thẳng hàng khi và chỉ khi $\overrightarrow{AB}$ cùng phương $\overrightarrow{AC}$ $ < = > \exists k \ne 0;k \in R$: $\overrightarrow{AB}=k\overrightarrow{AC}$ 

+ Nếu $\overrightarrow{AB}=k\overrightarrow{CD}$ và hai đường thẳng AB và CD phân biệt thì AB//CD.

Ví dụ 6: Cho tam giác ABC có trung tuyến AM. Gọi I là trung điểm AM và K là trung điểm AC sao $AK=\frac{1}{3}AC$ . Chứng minh ba điểm B, I, K thẳng hàng.

Hướng dẫn giải:

            Ta có

\[\begin{align} & 2\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{BM}=\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC} \\  & 4\overrightarrow{BI}=2\overrightarrow{BA}+\overrightarrow{BC}\,\,\,(1) \\ \end{align}\]

Ta lại có

\[\begin{align} & \overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}\, \\ & \,\,\,\,\,\,\,\,\,=\overrightarrow{BA}+\frac{1}{3}(\overrightarrow{BC}-\overrightarrow{BA})=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC} \\ & 3\overrightarrow{BK}=2\overrightarrow{BA}+\overrightarrow{BC}\,\,\,\,\,\,\,\,\,\,\,\,(2) \\ \end{align}\].

            Từ (1)&(2)=> $3\overrightarrow{BK}=4\overrightarrow{BI}\Rightarrow \overrightarrow{BK}=\frac{4}{3}\overrightarrow{BI}$=> B, I, K thẳng hàng.

Ví dụ 7: Cho tam giác ABC. Hai điểm M, N được xác định bởi hệ thức:

$\overrightarrow{BC}+\overrightarrow{MA}=\overrightarrow{0}$, $\overrightarrow{AB}-\overrightarrow{NA}-3\overrightarrow{AC}=\overrightarrow{0}$. Chứng minh MN//AC

Hướng dẫn giải:

$\begin{align} & \overrightarrow{BC}+\overrightarrow{MA}+\overrightarrow{AB}-\overrightarrow{NA}-3\overrightarrow{AC}=\overrightarrow{0} \\ & hay\,\,\overrightarrow{AC}+\overrightarrow{MN}-3\overrightarrow{AC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{MN}=2\overrightarrow{AC} \\ \end{align}$

$\overrightarrow{MN}//\overrightarrow{AC}$. Theo giả thiết $\overrightarrow{BC}=\overrightarrow{AM}$

Mà A,B,C không thẳng hàng nên bốn điểm A,B,C,M là hình bình hành

=> M không thuộc AC=> MN//AC

Dạng 4: Chứng minh đẳng thức vetơ có chứa tích của vectơ với một số

Ví dụ 8: Gọi M, N lần lượt là trung điểm của hai đoạn thẳng AB và CD. Chứng minh:              $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$

Hướng dẫn giải:

            \[\begin{align} & VP=\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NC}+\overrightarrow{BM}+\overrightarrow{MN}+\overrightarrow{ND} \\ & \,\,\,\,\,\,\,=\,2\overrightarrow{MN}+\overrightarrow{AM}+\overrightarrow{BM}+\overrightarrow{ND}+\overrightarrow{NC} \\ & \,\,\,\,\,\,=2\overrightarrow{MN} \\ \end{align}\]

Ví dụ 9: Cho hình bình hành ABCD. Chứng minh: $\overrightarrow{AB}+2\overrightarrow{AC}+\overrightarrow{AD}=3\overrightarrow{AC}$.

Hướng dẫn giải:

Áp dụng qui tắc hình bình hành ta có: \[\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\]

=> VT=$\overrightarrow{AC}+2\overrightarrow{AC}=3\overrightarrow{AC}=\overrightarrow{VP}$. (đpcm)

Ví dụ 10: Chứng minh rằng nếu G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’ thì $3\overrightarrow{GG’}=\overrightarrow{AA’}+\overrightarrow{BB’}+\overrightarrow{CC’}$.

Hướng dẫn giải:

\[\begin{align} & VP=\overrightarrow{AA’}+\overrightarrow{BB’}+\overrightarrow{CC’} \\ & \,\,\,\,\,\,\,=\overrightarrow{AG}+\overrightarrow{GG’}+\overrightarrow{G’A’}+\overrightarrow{BG}+\overrightarrow{GG’}+\overrightarrow{G’B’}+\overrightarrow{CG}+\overrightarrow{GG’}+\overrightarrow{G’C’} \\ & \,\,\,\,\,\,=3\overrightarrow{GG’}+\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}+\overrightarrow{G’A’}+\overrightarrow{G’B’}+\overrightarrow{G’C’} \\ & \,\,\,\,\,\,=3\overrightarrow{GG’}-(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC})+\overrightarrow{G’A’}+\overrightarrow{G’B’}+\overrightarrow{G’C’} \\ & \,\,\,\,\,\,=3\overrightarrow{GG’} \\ \end{align}\]

Dạng 5: Xác định vị trí của một điểm nhờ đẳng thức véctơ

  + $\overrightarrow{AB}=\overrightarrow{0}\Leftrightarrow A\equiv B$           

+ Cho điểm A và $\overrightarrow{a}$. Có duy nhất M sao cho : $\overrightarrow{AM}=\overrightarrow{a}$        

+ $\overrightarrow{AB}=\overrightarrow{AC}\Leftrightarrow B\equiv C;\,\,\,\overrightarrow{AD}=\overrightarrow{BD}\Leftrightarrow A\equiv B$

Ví dụ 11: Cho tam giác ABC có D là trung điểm BC. Xác định vị trí của G biết $\overrightarrow{AG}=2\overrightarrow{GD}$.

Hướng dẫn giải:

$\overrightarrow{AG}=2\overrightarrow{GD}$=> A,G, D thẳng hàng.

AG=2GD và G nằm giữa A và D.

Vậy G là trọng tâm tam giác ABC.

Ví dụ 12: Cho hai điểm A và B. Tìm điểm I sao cho: $\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{0}$.

Hướng dẫn giải:

$\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{0}\Leftrightarrow \overrightarrow{IA}=-2\overrightarrow{IB}\Rightarrow \left| \overrightarrow{IA} \right|=\left| -2\overrightarrow{IB} \right|$

hay IA=2IB, $\overrightarrow{IA}\uparrow \downarrow \overrightarrow{IB}$. Vậy I là điểm thuộc AB sao cho IB=$\frac{1}{3}$AB

Ví dụ 13: Cho tứ giác ABCD. Xác định vị trí điểm G sao cho: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$

Hướng dẫn giải:

Ta có : $\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GI}$, trong đó I là trung điểm AB

Tương tự: $\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GK}$, K là trung điểm CD

            => G là trung điểm IK.