Tích vô hướng của hai vectơ

1. Góc giữa hai vectơ

Cho hai vectơ $\vec a$ và $\vec b$. Từ điểm 0 bất kỳ, dựng $\vec OA$ = $\vec a$ . $\vec OB$ = $\vec b$.

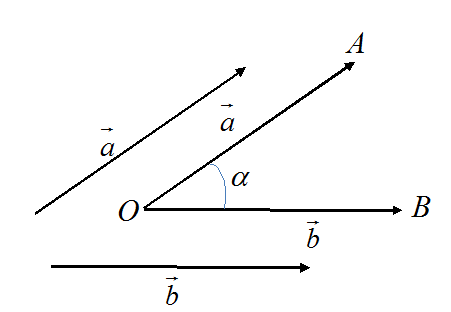
Khi đó: số đo $\widehat {AOB} = \alpha $ gọi là số đo của góc giữa hai vectơ $\vec a$ và $\vec b$.

Đặc biệt: Nếu $\widehat {AOB} = \alpha = {90^0}$, ta nói $\vec a$ vuông góc với $\vec b$, kí hiệu: $\overrightarrow a \bot \overrightarrow b $.

2. Định nghĩa tích vô hướng của hai vectơ

Định nghĩa: Tích vô hướng của hai vectơ $\vec a$ và $\vec b$ là một số , được kí hiệu là $\vec a.\vec b$ và được xác định bởi công thức:

$\vec a.\vec b=|\vec a|.|\vec b|.cos\left ( \vec a,\vec b \right )$

3. Tính chất của tích vô hướng

a) Định lí

Với ba vectơ $\vec a,\vec b,\vec c$ tùy ý và một số thực k, ta có:

+ $\vec a.\vec b=\vec b.\vec a$ (tính chất giao hoán)

+ $\vec a.\vec b=0\Leftrightarrow \vec a\perp \vec b$

+ $(k\vec a).\vec b=\vec a.(k\vec b)=k.(\vec a.\vec b)$

+ $\vec a. (\vec b\pm \vec c)=\vec a.\vec b\pm \vec a.\vec c$ (tính chất phân phối)

b) Hệ quả

Hệ quả 1: Bình phương vô hướng

Với mỗi vectơ $\vec a$ tùy ý, tích vô hướng $\vec a.\vec a$ được kí hiệu là $|\vec a|^2$ được gọi là bình phương vô hướng.

Như vậy: Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.

Hệ quả 2: Hằng đẳng thức véc tơ

$\begin{array}{l}
+ {{\vec a}^2} \ge 0;{{\vec a}^2} = 0 \Leftrightarrow \vec a = \vec 0\\
+ {\left( {\vec a + \vec b} \right)^2} = {{\vec a}^2} + 2\vec a.\vec b + {{\vec b}^2}\\
+ {\left( {\vec a – \vec b} \right)^2} = {{\vec a}^2} – 2\vec a.\vec b + {{\vec b}^2}\\
+ {{\vec a}^2} – {{\vec b}^2} = \left( {\vec a – \vec b} \right)\left( {\vec a + \vec b} \right)
\end{array}$

Hệ quả 3. Dấu của tích vô hướng

$ + \vec a.\vec b > 0 \Leftrightarrow 0^0 < \left( {\overrightarrow a ,\overrightarrow b } \right) < {90^0}$

$ + \vec a.\vec b < 0 \Leftrightarrow {90^0} < \left( {\overrightarrow a ,\overrightarrow b } \right) < {180^0}$

Chứng minh:

Ta có: $\vec a.\vec b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$.

Do: $\left| {\overrightarrow a } \right| > 0;\left| {\overrightarrow b } \right| > 0$

nên: $\vec a.\vec b > 0 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) > 0$

$ \Leftrightarrow {0^0} < \left( {\overrightarrow a ,\overrightarrow b } \right) < {90^0}$.

Góc $\left( {\vec a,\vec b} \right)$ nhọn.

Tương tự: $\left( {\overrightarrow a ,\overrightarrow b } \right) < 0 \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) > 0$

$ \Leftrightarrow {90^0} < \left( {\overrightarrow a ,\overrightarrow b } \right) < {180^0}$.

Góc $\left( {\overrightarrow a ,\overrightarrow b } \right)$ tù.

Hệ quả 4: Công thức tính công A của một lực tác động $\overrightarrow F $.

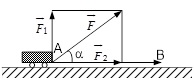
$\left| {\overrightarrow F } \right|.\left| {\overrightarrow {AB} } \right|.\cos \varphi $

Chứng minh

Ta có: $\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} $

$A = \overrightarrow F .\overrightarrow {AB}= \left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right)\overrightarrow {AB}= \overrightarrow {{F_2}} .\overrightarrow {AB} $

$\left| {\overrightarrow {{F_2}} } \right|.\left| {\overrightarrow {AB} } \right|$

$ = \left| {\overrightarrow F } \right|.\left| {\overrightarrow {AB} } \right|\cos \varphi $

4. Biểu thức tọa độ của tích vô hướng

Cho hai vectơ $\vec a(x;y);\vec b(x’;y’)$. Khi đó:

+ $\vec{a}.\vec{b}=xx’+yy’$
+ $|\vec{a}|=\sqrt{x^2+y^2}$
+ $cos(\vec a;\vec b) = \frac{{xx’ + yy’}}{{\sqrt {{x^2} + {y^2}} .\sqrt {{{x’}^2} + {{y’}^2}} }},(\vec a \ne \vec 0;\vec b \ne \vec 0)$
+ $\vec{a}\perp \vec{b}\Leftrightarrow xx’+yy’=0$

Hệ quả

Hệ quả 1. Độ dài của vectơ

Cho $\vec{a}$ = (a₁, a₂)

$\left| {\vec{a}} \right|=\sqrt{a_{1}^{2}+a_{2}^{2}}$

Ví dụ: $\overrightarrow {AB} = \left( {-1;-2} \right),\;\overrightarrow {AC} = \left( {4;–2} \right)$. Tính $\left| {\overrightarrow {AB} } \right|$;$\left| {\overrightarrow {AC} } \right|$

Giải

$AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {–1} \right)}^2} + {{\left( {–2} \right)}^2}} = \sqrt 5 $

$AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{4^2} + {{\left( {–2} \right)}^2}} = 2\sqrt 5 $

Hệ quả 2. Xác định Góc giữa hai vectơ khi biết tọa độ của hai véc tơ

Cho $\vec{a}$ = (a₁, a₂), $\vec{b}$ = (b₁, b₂) ($\vec{a},\vec{b}\ne \vec{0}$)

$\cos \left( {\vec a,\vec b} \right) = \frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}} = \frac{{{a_1}{b_1} + {a_2}{b_2}}}{{\sqrt {a_1^2 + a_2^2} .\sqrt {b_1^2 + b_2^2} }}$

Ví dụ: Cho $\overrightarrow{OM}$ = (–2; –1), $\overrightarrow{ON}$ = (3; –1). Tính $\widehat{MON}$ ?

Giải

Ta có: $\cos \left( {\vec a,\vec b} \right) = \frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}$

cos$\widehat{MON}$ = cos$\left( \overrightarrow{OM},\overrightarrow{ON} \right)$

= $\frac{\overrightarrow{OM}.\overrightarrow{ON}}{\left| \overrightarrow{OM} \right|.\left| \overrightarrow{ON} \right|}$

= $\frac{-6+1}{\sqrt{5}.\sqrt{10}}$

$=-\frac{\sqrt{2}}{2}$ Þ $\widehat{MON}$ = 135⁰

Hệ quả 3. Khoảng cách giữa hai điểm

Cho A(x_A; y_A), B(x_B; y_B)

AB =$\sqrt{{{({{x}_{B}}-{{x}_{A}})}^{2}}+{{({{y}_{B}}-{{y}_{A}})}^{2}}}$

Ví dụ: Cho M(–2; 2), N(1; 1). Tính MN ?

Giải: $\overrightarrow{AB}$ = (x_B – x_A; y_B – y_A)

MN = $\sqrt{{{(1+2)}^{2}}+{{(1-2)}^{2}}}$ $=\sqrt{10}$

5. Bài tập minh họa

Bài 1: Tính tích vô hướng của $\vec{a}(2;3)$ và $\vec{b}(1;1)$ biết chúng tạo với nhau một góc $30^o$.

Giải:

Áp dụng công thức tính tích vô hướng của hai vectơ, ta có:

$\vec{a}.\vec{b}=|\vec{a}|.|\vec{b}|.cos30^0$

$=\sqrt{2^2+3^2}.\sqrt{1^2+1^2}.\frac{\sqrt{3}}{2}=\frac{\sqrt{78}}{2}$

Bài 2: Cho hình vuông ABCD cạnh a đường chéo BD. Tính các tích vô hướng sau: $\vec{AD}.\vec{AB}$, $\vec{AD}.\vec{BD}$ và $\vec{AB}.\vec{CD}$ .

Vì $AD\perp AB$ nên $\vec{AD}.\vec{AB}=0$

$\vec{AD}.\vec{BD}=|\vec{AD}|.|\vec{BD}|cosADB=a.a\sqrt{2}.cos45=a^2$

$\vec{AB}.\vec{CD}=|\vec{AB}|.|\vec{CD}|.cos0^o=a^2$

Bài 3. Cho tam giác ABC đều cạnh a, đường cao AH. Tính:

a) $\overrightarrow{AB}.\overrightarrow{AC}$

b) $\overrightarrow{AB}.\overrightarrow{BC}$

c) $\overrightarrow{AH}.\overrightarrow{BC}$

Giải

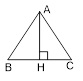
a) $\overrightarrow{AB}.\overrightarrow{AC}$ = a.a.cos60⁰ = $\frac{{{a}^{2}}}{2}$

b) $\overrightarrow{AB}.\overrightarrow{BC}$ = a.a.cos120⁰=–$\frac{{{a}^{2}}}{2}$

c) $\overrightarrow{AH}.\overrightarrow{BC}$ = 0

Bài 4. Cho tam giác ABC vuông tại A, AB = c, AC = b. Tính:

a) $\overrightarrow{BA}.\overrightarrow{BC}$

b) $\overrightarrow{CA}.\overrightarrow{CB}$

Giải

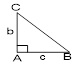
a) cos($\overrightarrow{BA},\overrightarrow{BC}$) = $\frac{c}{\sqrt{{{b}^{2}}+{{c}^{2}}}}$

=> $\overrightarrow{BA}.\overrightarrow{BC}$ = c²

b)
$\begin{array}{l}
\cos \left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = \frac{b}{{\sqrt {{b^2} + {c^2}} }}\\
\Rightarrow \overrightarrow {CA} .\overrightarrow {CB} = b.\sqrt {{b^2} + {c^2}} .\frac{b}{{\sqrt {{b^2} + {c^2}} }} = {b^2}
\end{array}$

Bài 5. Cho tam giác ABC đều cạnh a. Tính:

$\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} $

Đáp số: $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} = – \frac{{3{a^2}}}{2}$

6. Bài tập vân dụng

Cho A(1; 1), B(2; 3), C(–1; –2).

a) Xác định điểm D sao cho ABCD là hình bình hành.

b) Tính chu vi hbh ABCD.

c) Tính góc A.

Hướng dẫn

ABCD là hình bình hành khi và chi khi:
$\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}
{x_D} = – 2\\
{y_D} = – 4
\end{array} \right.$

b) AB = $\sqrt{{{1}^{2}}+{{2}^{2}}}=\sqrt{5}$

AD = $\sqrt{{{3}^{2}}+{{5}^{2}}}=\sqrt{34}$

cosA = cos$\left( \overrightarrow{AB},\overrightarrow{AD} \right)$
= $\frac{\overrightarrow{AB}.\overrightarrow{AD}}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{AD} \right|}$
= $\frac{-3-10}{\sqrt{5}.\sqrt{34}}=-\frac{13}{\sqrt{170}}$

Củng cố lý thuyết qua sơ đồ tư duy

https://youtu.be/xuMwYKwWsdQ

Trắc nghiệm

Câu 1: Cho vectơ $\vec{a}(4;3)$ và vectơ $\vec{b}(-3;4)$. Góc hợp bởi 2 vectơ trên là $90^o$. Tích vô hướng của hai vectơ là:

A. 0
B. $\frac{25}{2}$
C. $\frac{25\sqrt{3}}{2}$
D. $5\sqrt{2}$

Câu 2: Cho $\vec a(1;3)$ và $\vec b( – 2;4)$. Góc tạo bởi hai vectơ trên là:

A. $30^o$
B. $45^o$
C. $60^o$
D. $75^o$

Câu 3: Chu vi của tam giác ABC có tọa độ ba điểm lần lượt là (A(1;1);B(2;6);C(-2;4)) bằng?

A. $\approx 10,219$
B. $\approx 13,813$
C. $\approx 14,767$
D. $\approx 17,532$

Câu 3: Cho hai vectơ $\vec a = 2\vec i + \vec j$ và $\vec b = k\vec i – \vec j$ . Giá trị của k để $\vec a \bot \vec b$ là:

A. $k=\frac{1}{3}$
B. $k=\frac{-1}{3}$
C. $k=\frac{1}{2}$
D. $k=\frac{-1}{2}$

Câu 4. Cho hình bình hành ABCD có độ dài các đường chéo AC= 6, BD= 8. Giá trị của tích vô hướng của vecto AB nhân vecto AD là:

A.5 B.-7 C.7 D.25

Bài tập tự luận

Bài 1. Cho tam giác ABC không cân. Đường tròn tâm I nội tiếp tam giác , tiếp xúc với các cạnh BC, CA, AB lần lượt tại A’, B’, C’ . Đường thằng B’C’ cắt BC tại D. Chứng minh ID vuông góc với AA’

Bài 2. Cho hình chữ nhật ABCD. Gọi E là hình chiếu cuarB trên AC, F và G là trung điểm của AE và CD. Chứng minh BF vuông góc với FG

——————

Download tài liệu: PDF-tại đây Word: tại đây.

Xem thêm:

———————–

User

Tích vô hướng của hai vectơ

Đăng bởi ADMIN vào 29/11/201929/11/2019