HÃY THỬ SỨC VỚI ĐỀ LUYỆN TẬP SAU
Đề gồm 50 câu trắc nghiệm
HƯỚNG DẪN VÀ LỜI GIẢI
Câu 1. Tìm số phức liên hợp của số phức $z=-i$.
A. $\bar{z}=i$. B. $\bar{z}=1$. C. $\bar{z}=-i$. D. $\bar{z}=-1$.
Lời giải
Chọn A
Câu 2. Cho số phức $z=-2+3i$. Số phức liên hợp của $z$ là?
A. $\bar{z}=\sqrt{13}$. B. $\bar{z}=2-3i$. C. $\bar{z}=3-2i$. D. $\bar{z}=-2-3i$.
Lời giải
Chọn D
$\bar{z}=-2-3i$.
Câu 3. Số phức $z$ thỏa mãn $\overline{z}=-3-2i$ là
A. $z=-3-2i$ B. $z=-3+2i$ C. $z=3-2i$ D. $z=3+2i$
Lời giải
Chọn B
Ta có $\overline{z}=-3-2i$ suy ra $z=-3+2i$.
Câu 4. Tìm số phức liên hợp của số phức $z=\left( 2+i \right)\left( -3i \right).$
A. $\bar{z}=3-6i$. B. $\bar{z}=3+6i$. C. $\bar{z}=-3+6i$. D. $\bar{z}=-3-6i$.
Lời giải
Chọn B
Ta có: $z=\left( 2+i \right)\left( -3i \right)=3-6i$$\Rightarrow \bar{z}=3+6i$.
Câu 5. Tìm số phức liên hợp của số phức $z=\left( 2-3i \right)\left( 3+2i \right)$.
A. $\overline{z}=12-5i$. B. $\overline{z}=-12+5i$. C. $\overline{z}=-12-5i$. D. $\overline{z}=12+5i$.
Lời giải:
Chọn D
Ta có $z=\left( 2-3i \right)\left( 3+2i \right)$$=6-5i-6{{i}^{2}}=12-5i$$\Rightarrow \overline{z}=12+5i$.
Câu 6. Tìm số phức liên hợp của số phức $z=3\left( 2+3i \right)-4\left( 2i-1 \right)$.
A. $10+i$. B. $-10-i$. C. $1-10i$. D. $10-i$.
Lời giải:
Chọn D
Ta có: $z=3(2+3i)-4(2i-1)=6+9i-8i+4=10+i\Rightarrow \overline{z}=10-i$.
Câu 7. Tìm số phức liên hợp của số phức $z$ biết $z=i.z+2$.
A. $1-i$. B. $-1+i$. C. $-1-i$. D. $1+i$.
Lời giải:
Chọn A
Ta có $z=i.z+2\Leftrightarrow z=\frac{2}{1-i}=\frac{2\left( 1+i \right)}{2}=1+i$. Vậy $\bar{z}=1-i$.
Câu 8. Cho các số phức ${{z}_{1}}=2+3i$, ${{z}_{2}}=4+5i$. Số phức liên hợp của số phức $w=2\left( {{z}_{1}}+{{z}_{2}} \right)$ là
A. $\bar{w}=28i$. B. $\bar{w}=8+10i$. C. $\bar{w}=12-16i$. D. $\bar{w}=12+8i$.
Lời giải:
Chọn C
Ta có $w=2\left( 6+8i \right)=12+16i\Rightarrow \bar{w}=12-16i$.
Câu 9. Kí hiệu $a,b$ lần lượt là phần thực và phần ảo của số phức $z=-4-3i$. Tìm $a,b$.
A. $a=4$, $b=3$. B. $a=-4$, $b=-3i$. C. $a=-4$, $b=3$. D. $a=-4$, $b=-3$.
Lời giải:
Chọn D
Câu 10. Cho điểm $M$ là điểm biểu diễn của số phức $z$. Tìm phần thực và phần ảo của số phức $z$.
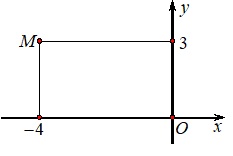
A. Phần thực là $3$ và phần ảo là $-4$. B. Phần thực là $-4$ và phần ảo là $3i$.
C. Phần thực là $3$ và phần ảo là $-4i$. D. Phần thực là $-4$ và phần ảo là $3$.
Lời giải:
Chọn D
Câu 11. Cho số phức $z$ có số phức liên hợp $\bar{z}=3-2i$. Tổng phần thực và phần ảo của số phức $z$ bằng.
A. $-1$. B. $1$. C. $-5$. D. $5$.
Lời giải:
Chọn D
Ta có: $z=3+2i$. Vậy tổng phần thực và phần ảo của số phức $z$ bằng $5$.
Câu 12. Cho số phức $z=3-2i$. Tìm phần ảo của của số phức liên hợp $z$.
A. $-2i$. B. $-2$. C. $2$. D. $2i$.
Lời giải:
Chọn C
Ta có: $\overline{z}=3+2i\Rightarrow $ phần ảo của $\overline{z}$ là $2$.
Câu 13. Cho số phức ${{z}_{1}}=1+2i$ và ${{z}_{2}}=2-3i$. Phần thực và phần ảo của số phức ${{z}_{1}}-2{{z}_{2}}$ là.
A. Phần thực là $-3$ và phần ảo là $8i$. B. Phần thực là $-3$ và phần ảo là $8$.
C. Phần thực là $-3$ và phần ảo là $-8$. D. Phần thực là $3$ và phần ảo là $8$.
Lời giải:
Chọn B
Ta có: ${{z}_{1}}-2{{z}_{2}}=1+2i-2\left( 2-3i \right)=-3+8i$. Vậy phần thực của ${{z}_{1}}-2{{z}_{2}}$là $-3$ và phần ảo là $8$.
Câu 14. Cho số phức $z=1-\sqrt{2}i$. Tìm phần ảo của số phức $P=\frac{1}{\overline{z}}$.
A. $-\sqrt{2}$. B. $-\sqrt{2}$. C. $-\frac{\sqrt{2}}{3}$. D. $-\frac{\sqrt{2}}{3}$.
Lời giải:
Chọn C
Ta có: $P=\frac{1}{\overline{z}}=\frac{1}{1+i\sqrt{2}}=\frac{1-i\sqrt{2}}{{{1}^{2}}+{{\sqrt{2}}^{2}}}=\frac{1-i\sqrt{2}}{3}=\frac{1}{3}-\frac{\sqrt{2}}{3}i$.
B. Mức độ 2
Câu 1. Cho số phức $z$ thoả mãn $\frac{z}{3+2i}=1-i$ Số phức liên hợp $\bar{z}$ là.
A. $\bar{z}=5+i$. B. $\bar{z}=-5-i$. C. $\bar{z}=-1-5i$. D. $\bar{z}=-1+5i$.
Lời giải
Chọn A
$z=\left( 3+2i \right)\left( 1-i \right)=5-i$.
Số phức liên hợp $\bar{z}=5+i$.
Câu 2. Tìm số phức liên hợp của số phức $z=\left( 2+i \right)\left( -1+i \right){{\left( 2i+1 \right)}^{2}}$.
A. $\bar{z}=5+15i$. B. $\bar{z}=5+5i$. C. $\bar{z}=1+3i$. D. $\bar{z}=5-15i$.
Lời giải:
Chọn A
$z=(2+i)(-1+i){{(2i+1)}^{2}}=\left( -3+i \right)\left( -3+4i \right)=5-15i$$\Rightarrow \bar{z}=5+15i$.
Câu 3. Số phức liên hợp của số phức $z=\frac{{{\left( 1-\sqrt{3}i \right)}^{3}}}{1-i}$ là
A. $\overline{z}=-4+4i$. B. $\overline{z}=4-4i$. C. $\overline{z}=-4-4i$. D. $\overline{z}=4+4i$.
Lời giải
Chọn A
Ta có: $z=\frac{{{\left( 1-\sqrt{3}i \right)}^{3}}}{1-i}$$=\frac{{{\left( 1-\sqrt{3}i \right)}^{3}}\left( 1+i \right)}{\left( 1-i \right)\left( 1+i \right)}$$=-4-4i$. Suy ra $\overline{z}=-4+4i$.
Câu 4. Tìm số phức $\bar{z}$ thỏa mãn $\frac{2+i}{1-i}z=\frac{-1+3i}{2+i}$.
A. $-\frac{22}{25}+\frac{4}{25}i$. B. $\frac{22}{25}+\frac{4}{25}i$. C. $\frac{22}{25}-\frac{4}{25}i$. D. $\frac{22}{25}i+\frac{4}{25}$.
Lời giải
Chọn C
Dùng máy tính: $z=\frac{22}{25}+\frac{4}{25}i$. Vậy $\bar{z}=\frac{22}{25}-\frac{4}{25}i$.
Câu 5. Cho hai số phức $z=1+3i$, $w=2-i$. Tìm phần ảo của số phức $u=\overline{z}.w$.
A. $5$. B. $-7i$. C. $-7$. D. $5i$.
Lời giải.
Chọn C
$\overline{z}=1-3i$; $u=\overline{z}.\text{w}=\left( 1-3i \right)\left( 2-i \right)=-1-7i$.
Vậy phần ảo của số phức $u$ bằng $-7$.
Câu 6. Cho số phức $z$ thỏa mãn $\left( 3+2i \right)z=7+5i$. Số phức liên hợp $\overline{z}$ của số phức $z$ là
A. $\overline{z}=\frac{31}{5}-\frac{1}{5}i$. B. $\overline{z}=\frac{31}{13}-\frac{1}{13}i$. C. $\overline{z}=-\frac{31}{13}+\frac{1}{13}i$. D. $\overline{z}=-\frac{31}{5}+\frac{1}{5}i$.
Lời giải
Chọn B
Ta có: $\left( 3+2i \right)z=7+5i$$\Rightarrow z=\frac{7+5i}{3+2i}=\frac{31}{13}+\frac{1}{13}i$.
Vậy $\overline{z}=\frac{31}{13}-\frac{1}{13}i$.
Câu 7. Cho số phức $z$ thỏa mãn: $\left( 1+i \right)z=14-2i$. Tổng phần thực và phần ảo của $\bar{z}$ bằng:
A. $-4$. B. $14$. C. $4$. D. $-14$.
Lời giải.
Chọn B
Ta có: $\left( 1+i \right)z=14-2i\Leftrightarrow z=\frac{14-2i}{1+i}=6-8i\Rightarrow \bar{z}=6+8i$
Vậy tổng phần thực phần ảo của $\bar{z}$ là $14$.
Câu 8. Cho số phức $z$ thỏa mãn: $(3+2i)z+{{(2-i)}^{2}}=4+i$. Hiệu phần thực và phần ảo của số phức $z$ là:
A. $0$ B. $2$ C. $1$ D. $3$.
Lời giải.
Chọn A
Ta có :
$(3+2i)z+{{(2-i)}^{2}}=4+i$$\Leftrightarrow (3+2i)z=4+i-{{\left( 2-i \right)}^{2}}$$\Leftrightarrow (3+2i)z=1+5i$$\Leftrightarrow z=\frac{1+5i}{3+2i}$$\Leftrightarrow z=1+i$
$\Rightarrow $ phần thực của số phức $z$ là $a=1$, phần ảo của số phức $z$ là $b=1$.
Vậy $a-b=0$.
Câu 9. Cho số phức $z$ thỏa mãn $\left( 4+7i \right)z-\left( 5-2i \right)=6iz$. Tìm phần ảo của số phức $z$?
A. $\frac{18}{17}$. B. $-\frac{18}{17}$. C. $-\frac{13}{17}$. D. $\frac{13}{17}$.
Lời giải:
Chọn C
$\left( 4+7i \right)z-\left( 5-2i \right)=6iz\Leftrightarrow \left( 4+i \right)z=5-2i\Leftrightarrow z=\frac{5-2i}{4+i}=\frac{\left( 5-2i \right)\left( 4-i \right)}{\left( 4+i \right)\left( 4-i \right)}=\frac{18-13i}{17}=\frac{18}{17}-\frac{13}{17}i$.
Câu 10. Cho số phức $z=1+2i$. Tìm phần thực và phần ảo của số phức $w=2z+\bar{z}$.
A. Phần thực là $2$ và phần ảo là $3$. B. Phần thực là $3$ và phần ảo là $2i$.
C. Phần thực là $2i$ và phần ảo là $3$. D. Phần thực là $3$ và phần ảo là $2$.
Lời giải:
Chọn D
$w=2z+\bar{z}=2\left( 1+2i \right)+\left( 1-2i \right)=3+2i$. Phần thực là $3$ và phần ảo là $2$.
Câu 11. Cho số phức $z=a+bi$. Số phức ${{z}^{2}}$ có phần ảo là?
A.$2ab$. B. ${{a}^{2}}{{b}^{2}}$. C. ${{a}^{2}}-{{b}^{2}}$. D. $2abi$.
Lời giải.
Chọn A
Ta có : ${{z}^{2}}={{\left( a+bi \right)}^{2}}={{a}^{2}}-{{b}^{2}}+2abi$. Phần ảo của ${{z}^{2}}$ là $2ab$.
Câu 12. Gọi ${{z}_{1}}$; ${{z}_{2}}$ là các nghiệm của phương trình ${{z}^{2}}-3z+5=0$. Mô đun của số phức $\left( 2\overline{{{z}_{1}}}-3 \right)\left( 2\overline{{{z}_{2}}}-3 \right)$ bằng
A. $7$. B. $11$. C. $29$. D. $1$.
Lời giải.
Chọn B
Phương trình ${{z}^{2}}-3z+5=0$ có nghiệm là $z=\frac{3}{2}\pm \frac{\sqrt{11}}{2}i$
Không mất tính tổng quát, giả sử: ${{z}_{1}}=\frac{3}{2}+\frac{\sqrt{11}}{2}i$ và ${{z}_{2}}=\frac{3}{2}-\frac{\sqrt{11}}{2}i$
Ta có: $\left( 2\overline{{{z}_{1}}}-3 \right)\left( 2\overline{{{z}_{2}}}-3 \right)=\left( 3-i\sqrt{11}-3 \right)\left( 3+i\sqrt{11}-3 \right)=\left( -i\sqrt{11} \right)\cdot i\sqrt{11}=-11{{i}^{2}}=11$
Vậy mô đun của số phức $\left( 2\overline{{{z}_{1}}}-3 \right)\left( 2\overline{{{z}_{2}}}-3 \right)$ bằng $11$.
Ä Mức độ 3
Câu 1. Có bao nhiêu số phức $z$ thỏa $\left| \frac{z+1}{i-z} \right|=1$ và $\left| \frac{z-i}{2+z} \right|=1?$
A. 1. B. 2. C. 3. D. $y=2$.
Lời giải:
Chọn A
Đặt $z=x+yi$ với $x,y\in \mathbb{R}$.
Ta có:
$\left\{ \begin{array}{l} \left| {\frac{{z + 1}}{{i – z}}} \right| = 1\\ \left| {\frac{{z – i}}{{2 + z}}} \right| = 1 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} \left| {z + 1} \right| = \left| {i – z} \right|\\ \left| {z – i} \right| = \left| {2 + z} \right| \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} \left| {x + 1 + yi} \right| = \left| { – x + \left( {1 – y} \right)i} \right|\\ \left| {x + \left( {y – 1} \right)i} \right| = \left| {x + 2 + yi} \right| \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} \sqrt {{{\left( {x + 1} \right)}^2} + {y^2}} = \sqrt {{{\left( { – x} \right)}^2} + {{\left( {1 – y} \right)}^2}} \\ \sqrt {{x^2} + {{\left( {y – 1} \right)}^2}} = \sqrt {{{\left( {x + 2} \right)}^2} + {y^2}} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = – y\\ 4x + 2y = – 3 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = – \frac{3}{2}\\ y = \frac{3}{2} \end{array} \right.$ $ \Rightarrow z = – \frac{3}{2} + \frac{3}{2}i.$Câu 2. Cho số phức $z={{\left( \frac{2+6i}{3-i} \right)}^{m}},\,$$m$ nguyên dương. Có bao nhiêu giá trị $m\in \left[ 1;50 \right]$ để $z$ là số thuần ảo?
A. 24. B. 26. C. 25. D. 50.
Lời giải
Chọn C
Ta có: $z={{\left( \frac{2+6i}{3-i} \right)}^{m}}={{(2i)}^{m}}={{2}^{m}}.{{i}^{m}}\,$
$z$ là số thuần ảo khi và chỉ khi $m=2k+1,\,\,k\in \mathbb{N}$ (do $z\ne 0;\text{ }\forall m\in {{\mathbb{N}}^{*}}$).
Vậy có 25 giá trị $m$ thỏa yêu cầu đề bài.
Câu 3. Có bao nhiêu số phức $z$ thỏa mãn $\left( 1+i \right)z+\overline{z}$ là số thuần ảo và $\left| z-2i \right|=1$.
A. $2$. B. $1$. C. $0$. D. Vô số.
Lời giải
Chọn A
Đặt $z=a+bi$ với $a,b\in \mathbb{R}$ ta có : ${{z}^{2}}={{x}^{2}}-{{y}^{2}}+2xy\text{i}$$=\left( 1+i \right)\left( a+bi \right)+a-bi$$=2a-b+ai$.
Mà $\left( 1+i \right)z+\overline{z}$ là số thuần ảo nên $2a-b=0$$\Leftrightarrow b=2a$. Mặt khác $\left| z-2i \right|=1$ nên ${{a}^{2}}+{{\left( b-2 \right)}^{2}}=1$$\Leftrightarrow {{a}^{2}}+{{\left( 2a-2 \right)}^{2}}=1$$\Leftrightarrow 5{{a}^{2}}-8a+3=0$
$ \Leftrightarrow \left[ \begin{array}{l} a = 1\\ a = \frac{3}{5} \end{array} \right.$Câu 4. Cho số phức $z={{\left( \frac{1+i\sqrt{3}}{1+i} \right)}^{3}}$. Tìm phần thực và phần ảo của số phức $\bar{z}$?
A. Phần thực bằng $2$ và phần ảo bằng $2i$. B. Phần thực bằng $2$ và phần ảo bằng $2$.
C. Phần thực bằng $2$ và phần ảo bằng $-2i$. D. Phần thực bằng $2$ và phần ảo bằng $-2$.
Lời giải
Chọn D
Ta có $z={{\left( \frac{1+i\sqrt{3}}{1+i} \right)}^{3}}=\frac{{{\left( 1+i\sqrt{3} \right)}^{3}}}{{{\left( 1+i \right)}^{3}}}=\frac{-8}{-2+2i}=2+2i\Rightarrow \bar{z}=2-2i$.
Câu 5. Cho số phức $z$ thỏa mãn điều kiện $\left( 3+2i \right)z+{{\left( 2-i \right)}^{2}}=4+i.$ Tìm phần ảo của số phức $w=\left( 1+z \right)\bar{z}$.
A. $-1$. B. $0$. C. $-i$. D. $-2$.
Lời giải:
Chọn A
Ta có $\left( 3+2i \right)z+{{\left( 2-i \right)}^{2}}=4+i$ $\Leftrightarrow $ $z=1+i$.
Do đó $w=\left( 1+z \right)\bar{z}=\left( 2+i \right)\left( 1-i \right)=3-i$ $\Rightarrow $ phần ảo của số phức $w=-1$.
Câu 6. Tìm phần ảo của số phức $z$ thỏa mãn $z+2\overline{z}={{\left( 2-i \right)}^{3}}\left( 1-i \right)$.
A. $-9$. B. $13$. C. $-13$. D. $9$.
Lời giải:
Chọn B
Ta có $z+2\overline{z}={{\left( 2-i \right)}^{3}}\left( 1-i \right)\Leftrightarrow z+2\overline{z}=-9-13i$. Đặt $z=a+bi\,\,\left( a,\,\,b\in \mathbb{R} \right)$. Khi đó $\left( a+bi \right)+2\left( a-bi \right)=-9-13i$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {3a = – 9}\\ { – b = – 13} \end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {a = – 3}\\ {b = 13} \end{array}} \right.$Câu 7. Nếu số phức $z\ne 1$ thoả mãn $\left| z \right|=1$ thì phần thực của $\frac{1}{1-z}$ bằng:
A. ${1}$. B. ${\frac{1}{2}}$. C. ${2}$. D. ${4}$.
Lời giải:
Chọn B
$z=x+yi\left( x,y\in \mathbb{R} \right)$, $\left| z \right|=1\Leftrightarrow {{x}^{2}}+{{y}^{2}}=1$.
$\frac{1}{1-z}=\frac{1}{1-x-yi}=\frac{1-x}{{{\left( 1-x \right)}^{2}}+{{y}^{2}}}+\frac{y}{{{\left( 1-x \right)}^{2}}+{{y}^{2}}}i$ có phần thực là.
$\frac{1-x}{{{\left( 1-x \right)}^{2}}+{{y}^{2}}}=\frac{1-x}{1-2x+{{x}^{2}}+{{y}^{2}}}=\frac{1-x}{2-2x}=\frac{1}{2}$.
Câu 8. Cho hai số phức ${{z}_{1}}$, ${{z}_{2}}$ thỏa mãn $\left| {{z}_{1}} \right|=1$, $\left| {{z}_{2}} \right|=2$ và $\left| {{z}_{1}}+{{z}_{2}} \right|=3$. Giá trị của $\left| {{z}_{1}}-{{z}_{2}} \right|$ là:
A. $0$. B. $1$. C. $2$. D. một giá trị khác.
Lời giải:
Chọn B
Giả sử ${{z}_{1}}={{a}_{1}}+{{b}_{1}}i,\,\,\,\,\left( {{a}_{1}},\,\,{{b}_{1}}\in \mathbb{R} \right)$, ${{z}_{2}}={{a}_{2}}+{{b}_{2}}i,\,\,\,\,\left( {{a}_{2}},\,\,{{b}_{2}}\in \mathbb{R} \right)$.
Theo bài ra ta có:
$\left\{ \begin{array}{l} \left| {{z_1}} \right| = 1\\ \left| {{z_2}} \right| = 2\\ \left| {{z_1} + {z_2}} \right| = 3 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a_1^2 + b_1^2 = 1\\ a_2^2 + b_2^2 = 4\\ {\left( {{a_1} + {a_2}} \right)^2} + {\left( {{b_1} + {b_2}} \right)^2} = 9 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a_1^2 + b_1^2 = 1\\ a_2^2 + b_2^2 = 4\\ 2{a_1}{a_2} + 2{b_1}{b_2} = 4 \end{array} \right.$Khi đó, ta có:
$\left| {{z}_{1}}-{{z}_{2}} \right|=\sqrt{{{\left( {{a}_{1}}-{{a}_{2}} \right)}^{2}}+{{\left( {{b}_{1}}-{{b}_{2}} \right)}^{2}}}$ $=\sqrt{\left( a_{1}^{2}+b_{1}^{2} \right)+\left( a_{2}^{2}+b_{2}^{2} \right)-\left( 2{{a}_{1}}{{a}_{2}}+2{{b}_{1}}{{b}_{2}} \right)}$ $=1$.
Vậy $\left| {{z}_{1}}-{{z}_{2}} \right|=1$.
Câu 9. Cho $2$ số phức ${{z}_{1}}$, ${{z}_{2}}$ thỏa $\left| {{z}_{1}} \right|=1$, $\left| {{z}_{2}} \right|=1$,$\left| {{z}_{1}}+{{z}_{2}} \right|=\sqrt{3}$. Khi đó $\left| {{z}_{1}}-{{z}_{2}} \right|$ bằng:
A. $2$. B. $\sqrt{3}$. C. $2-\sqrt{3}$. D. $1$.
Lời giải:
Chọn D
Giả sử ${{z}_{1}}=a+bi$, ${{z}_{2}}=c+di$ với $a$, $b$, $c$, $d\in \mathbb{R}$.
Ta có $\left| {{z}_{1}} \right|=1$$\Leftrightarrow \sqrt{{{a}^{2}}+{{b}^{2}}}=1$$\Leftrightarrow {{a}^{2}}+{{b}^{2}}=1$.
$\left| {{z}_{2}} \right|=1$$\Leftrightarrow \sqrt{{{c}^{2}}+{{d}^{2}}}=1$$\Leftrightarrow {{c}^{2}}+{{d}^{2}}=1$.
$\left| {{z}_{1}}+{{z}_{2}} \right|=\sqrt{3}$$\Leftrightarrow \sqrt{{{\left( a+c \right)}^{2}}+{{\left( b+d \right)}^{2}}}=\sqrt{3}$$\Leftrightarrow {{a}^{2}}+{{c}^{2}}+2ac+{{b}^{2}}+{{d}^{2}}+2bd=3$
$\Leftrightarrow {{a}^{2}}+{{c}^{2}}+{{b}^{2}}+{{d}^{2}}+2bd+2ac=3$$\Leftrightarrow 2bd+2ac=1$.
Khi đó $\left| {{z}_{1}}-{{z}_{2}} \right|$$=\sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$$=\sqrt{{{a}^{2}}+{{c}^{2}}+{{b}^{2}}+{{d}^{2}}-2bd-2ac}$$=1$.
Câu 10. Cho số phức $z=a+bi$ $\left( a,\text{ }b\in \mathbb{R} \right)$ thỏa mãn $z+1+3i-\left| z \right|i=0$. Tính $S=a+3b$.
A. $S=\frac{7}{3}$. B. $S=-5$. C. $S=5$. D. $S=-\frac{7}{3}$.
Lời giải:
Chọn B
Ta có $z+1+3i-\left| z \right|i=0$$\Leftrightarrow a+bi+1+3i-i\sqrt{{{a}^{2}}+{{b}^{2}}}=0$ $\Leftrightarrow a+1+\left( b+3-\sqrt{{{a}^{2}}+{{b}^{2}}} \right)i=0$
$ \Leftrightarrow \left\{ \begin{array}{l} a + 1 = 0\\ b + 3 = \sqrt {{a^2} + {b^2}} \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = – 1\\ \left\{ \begin{array}{l} b \ge – 3\\ {\left( {b + 3} \right)^2} = 1 + {b^2} \end{array} \right. \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = – 1\\ b = – \frac{4}{3} \end{array} \right.$$\Rightarrow S=-5$.
Câu 11. Có bao nhiêu số phức $z$ thỏa mãn $\left| z+1-3i \right|=3\sqrt{2}$ và ${{\left( z+2i \right)}^{2}}$ là số thuần ảo?
A. $1$. B. $2$. C. $3$. D. $4$.
Lời giải:
Chọn C
Gọi $z=x+yi\left( x,y\in \mathbb{R} \right)$, khi đó
$\left| z+1-3i \right|=3\sqrt{2}\Leftrightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=18\,\,\,\,\left( 1 \right)$.
${{\left( z+2i \right)}^{2}}={{\left[ x+\left( y+2 \right)i \right]}^{2}}={{x}^{2}}-{{\left( y+2 \right)}^{2}}+2x\left( y+2 \right)i$. Theo giả thiết ta có ${{x}^{2}}-{{\left( y+2 \right)}^{2}}=0$
$ \Leftrightarrow \left[ \begin{array}{l} x = y + 2\\ x = – \left( {y + 2} \right) \end{array} \right.$Trường hợp 1: $x=y+2$ thay vào $\left( 1 \right)$ ta được phương trình $2{{y}^{2}}=0$
và giải ra nghiệm $y=0$, ta được $1$ số phức ${{z}_{1}}=2$.
Trường hợp 2: $x=-\left( y+2 \right)$ thay vào $\left( 1 \right)$ ta được phương trình $2{{y}^{2}}-4y-8=0$ và giải ra ta được
$\left[ \begin{array}{l} y = 1 + \sqrt 5 \\ y = 1 – \sqrt 5 \end{array} \right.$ta được $2$ số phức
$\left[ \begin{array}{l} {z_2} = – 3 – \sqrt 5 + \left( {1 + \sqrt 5 } \right)i\\ {z_3} = – 3 + \sqrt 5 + \left( {1 – \sqrt 5 } \right)i \end{array} \right.$Vậy có $3$ số phức thỏa mãn yêu cầu bài toán.
Câu 12. Cho số phức ${z}$thỏa ${\overline{z}=\frac{{{\left( 1-i\sqrt{3} \right)}^{3}}}{1-i}}$. Môđun của số phức ${\overline{z}+iz}$ bằng.
A. ${8\sqrt{2}}$. B. ${2\sqrt{2}}$. C. ${4\sqrt{2}}$. D. ${\sqrt{2}}$.
Lời giải:
Chọn A
${\overline{z}=-4-4i\Rightarrow \overline{z}+iz=-8-8i\Rightarrow \left| \overline{z}+iz \right|=8\sqrt{2}}$.
Câu 13. Cho số phức $z$ thỏa điều kiện ${\frac{1+5i}{1+i}z+\bar{z}=10-4i}$. Tính môđun của số phức ${w=1+iz+{{z}^{2}}}$.
A. ${\left| w \right|=5}$. B. ${\left| w \right|=\sqrt{47}}$. C. ${\left| w \right|=6}$. D. ${\left| w \right|=\sqrt{41}}$.
Lời giải:
Chọn D
Gọi ${z=a+bi\left( a,b\in \mathbb{R} \right)}$. Khi đó ${\frac{1+5i}{1+i}z+\bar{z}=10-4i\Leftrightarrow \left( 1+5i \right)\left( a+bi \right)+\left( 1+i \right)\left( a-bi \right)=\left( 10-4i \right)\left( 1+i \right)}$.
$ \Leftrightarrow \left( {2a – 4b – 14} \right) + \left( {6a – 6} \right)i = 0$
$ \Leftrightarrow \left[ \begin{array}{l} a = 1\\ b = – 3 \end{array} \right.$$ \Rightarrow z = 1 – 3i$
suy ra ${w=1+i\left( 1-3i \right)+{{\left( 1-3i \right)}^{2}}=-4-5i}$.
vậy ${\left| w \right|=\sqrt{41}}$.
Câu 14. Biết số phức $z$ có phần ảo khác $0$ và thỏa mãn $\left| z-\left( 2+i \right) \right|=\sqrt{10}$ và $z.\bar{z}=25$. Điểm nào sau đây biểu diễn số phức $z$ trên?
A. $P\left( 4;\text{ }-3 \right)$ B. $N\left( 3;\text{ }-4 \right)$ C. $M\left( 3;\text{ }4 \right)$ D. $Q\left( 4;\text{ }3 \right)$
Lời giải:
Chọn C
Giả sử $z=x+yi$ $\left( x,y\in \mathbb{R},\text{ }y\ne 0 \right)$.
Ta có $\left| z-\left( 2+i \right) \right|=\sqrt{10}$$\Leftrightarrow \left| x+yi-\left( 2+i \right) \right|=\sqrt{10}$
$\Leftrightarrow \left| \left( x-2 \right)+\left( y-1 \right)i \right|=\sqrt{10}$$\Leftrightarrow {{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=10$$\Leftrightarrow {{x}^{2}}+{{y}^{2}}-4x-2y=5$.
Lại có $z.\bar{z}=25$$\Leftrightarrow {{x}^{2}}+{{y}^{2}}=25$ nên $25-4x-2y=5$$\Leftrightarrow 2x+y=10$$\Leftrightarrow y=10-2x$
$\Rightarrow {{x}^{2}}+{{\left( 10-2x \right)}^{2}}=25$$\Leftrightarrow 5{{x}^{2}}-40x+75=0$
$ \Leftrightarrow \left[ \begin{array}{l} x = 5\\ x = 3 \end{array} \right.$+ Với $x=5\Rightarrow y=0$, không thỏa mãn vì $y\ne 0$.
+ Với $x=3\Rightarrow y=4$, thỏa mãn $y\ne 0$$\Rightarrow z=3+4i$.
Do đó điểm $M\left( 3;\text{ }4 \right)$ biểu diễn số phức $z$.
Câu 15. Cho số phức $z=a+bi$ $\left( a,b\in \mathbb{R},a>0 \right)$ thỏa mãn $\left| z-1+2i \right|=5$ và $z.\bar{z}=10$. Tính $P=a-b$.
A. $P=4$ B. $P=-4$ C. $P=-2$ D. $P=2$
Lời giải:
Chọn C Từ giả thiết $\left| z-1+2i \right|=5$ và $z.\bar{z}=10$ ta có hệ phương trình
$\left\{ \begin{array}{l} {\left( {a – 1} \right)^2} + {\left( {b + 2} \right)^2} = 25\\ {a^2} + {b^2} = 10 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a – 2b = – 5\\ {a^2} + {b^2} = 10 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} a = 2b – 5\\ {\left( {2b – 5} \right)^2} + {b^2} = 10 \end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l} a = – 3\\ b = 1 \end{array} \right.$(loại) hay
$\left\{ \begin{array}{l} a = 1\\ b = 3 \end{array} \right.$Vậy $P=-2$.
Câu 16. Số phức $z=a+bi$ ( với $a$, $b$ là số nguyên) thỏa mãn $\left( 1-3i \right)z$ là số thực và $\left| \overline{z}-2+5i \right|=1$. Khi đó $a+b$ là
A. $9$ B. $8$ C. $6$ D. $7$
Lời giải:
Chọn B
Ta có: $\left( 1-3i \right)z$$=\left( 1-3i \right)\left( a+bi \right)$$=a+3b+\left( b-3a \right)i$.
Vì $\left( 1-3i \right)z$ là số thực nên $b-3a=0$$\Rightarrow b=3a$ $\left( 1 \right)$.
$\left| \overline{z}-2+5i \right|=1$$\Leftrightarrow \left| a-2+\left( 5-b \right)i \right|=1$$\Leftrightarrow {{\left( a-2 \right)}^{2}}+{{\left( 5-b \right)}^{2}}=1$ $\left( 2 \right)$. Thế $\left( 1 \right)$ vào $\left( 2 \right)$ ta có: ${{\left( a-2 \right)}^{2}}+{{\left( 5-3a \right)}^{2}}=1$$\Leftrightarrow 10{{a}^{2}}-34a+28=0$
$ \Leftrightarrow \left[ \begin{array}{l} a = 2 \Rightarrow b = 6\\ a = \frac{7}{5}{\rm{ (}}loa\”i i) \end{array} \right.$Vậy $a+b=2+6=8$.
Ä Mức độ 4
Câu 1. Cho số phức $w=1+\left( 1+i \right)+{{\left( 1+i \right)}^{2}}+{{\left( 1+i \right)}^{3}}+…+{{\left( 1+i \right)}^{20}}$. Tìm phần thực và phần ảo của số phức $\bar{w}$.
A. Phần thực bằng $-{{2}^{10}}$ và phần ảo bằng $\left( 1+{{2}^{10}} \right)$.
B. Phần thực bằng $-{{2}^{10}}$ và phần ảo bằng $-\left( 1+{{2}^{10}} \right)$.
C. Phần thực bằng ${{2}^{10}}$ và phần ảo bằng $\left( 1+{{2}^{10}} \right)$.
D. Phần thực bằng ${{2}^{10}}$ và phần ảo bằng $-\left( 1+{{2}^{10}} \right)$.
Lời giải
Chọn B
Ta có ${{\left( 1+i \right)}^{20}}={{\left( 2i \right)}^{10}}=-{{2}^{10}}\Rightarrow {{\left( 1+i \right)}^{21}}=-{{2}^{10}}-{{2}^{10}}i$.
Suy ra $w=\frac{\left[ 1-{{\left( 1+i \right)}^{21}} \right]}{-i}=\frac{1+{{2}^{10}}}{-i}+\frac{{{2}^{10}}i}{-i}=-{{2}^{10}}+\left( 1+{{2}^{10}} \right)i\Rightarrow \bar{w}=-{{2}^{10}}-\left( 1+{{2}^{10}} \right)i$.
Vậy $\bar{w}$ có phần thực bằng $-{{2}^{10}}$ và phần ảo bằng $-\left( 1+{{2}^{10}} \right)$.
Câu 2. Cho số phức $z\ne 0$ thỏa mãn $\frac{iz-\left( 3i+1 \right)\overline{z}}{1+i}={{\left| z \right|}^{2}}$. Số phức $w=\frac{13}{3}iz$ có môđun bằng:
A. $26$. B. $\sqrt{26}$. C. $\frac{3\sqrt{26}}{2}$. D. $13$.
Lời giải
Chọn C
Gọi $z=a+bi\left( a,b\in \mathbb{R} \right)$. Suy ra $\overline{z}=a-bi$.
Ta có $\frac{iz-\left( 3i+1 \right)\overline{z}}{1+i}={{\left| z \right|}^{2}}\Leftrightarrow \frac{i\left( a+bi \right)-\left( 3i+1 \right)\left( a-bi \right)}{1+i}={{a}^{2}}+{{b}^{2}}$
$\Leftrightarrow ai-b-3ai-3b-a+bi={{a}^{2}}+{{b}^{2}}+{{a}^{2}}i+{{b}^{2}}i$
$\Leftrightarrow \left( {{a}^{2}}+{{b}^{2}}+2a-b \right)i+\left( {{a}^{2}}+{{b}^{2}}+4b+a \right)=0$
$ \Leftrightarrow \left\{ \begin{array}{l} {a^2} + {b^2} + 2a – b = 0\\ {a^2} + {b^2} + a + 4b = 0 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} 26{b^2} + 9b = 0\\ a = 5b \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} b = 0,a = 0\\ b = \frac{{ – 9}}{{26}},a = \frac{{ – 45}}{{26}} \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} z = 0\\ z = \frac{{ – 45}}{{26}}i – \frac{9}{{26}} \end{array} \right.$$\Rightarrow z=\frac{-45}{26}i-\frac{9}{26}$ (Vì $z\ne 0$).
Với $z=\frac{-45}{26}i-\frac{9}{26}\Rightarrow \text{w}=\frac{15}{2}-\frac{3}{2}i\Rightarrow \left| \text{w} \right|=\frac{3\sqrt{26}}{2}$.
Câu 3. Cho hai số phức $z$, $w$ thỏa mãn $\left| z+2w \right|=3$, $\left| 2z+3w \right|=6$ và $\left| z+4w \right|=7$. Tính giá trị của biểu thức $P=z.\overline{w}+\overline{z}.w$.
A. $P=-14i$. B. $P=-28i$. C. $P=-14$. D. $P=-28$.
Lời giải
Chọn D
Ta có: $\left| z+2w \right|=3$\[\Leftrightarrow {{\left| z+2w \right|}^{2}}=9\]$\Leftrightarrow \left( z+2w \right).\left( \overline{z+2w} \right)=9$$\Leftrightarrow \left( z+2w \right).\left( \overline{z}+2\overline{w} \right)=9$
$\Leftrightarrow z.\overline{z}+2\left( z.\overline{w}+\overline{z}.w \right)+4w.\overline{w}=9$$\Leftrightarrow {{\left| z \right|}^{2}}+2P+4{{\left| w \right|}^{2}}=9$ $\left( 1 \right)$.
Tương tự:
$\left| 2z+3w \right|=6$$\Leftrightarrow {{\left| 2z+3w \right|}^{2}}=36$$\Leftrightarrow \left( 2z+3w \right).\left( 2\overline{z}+3\overline{w} \right)=36$$\Leftrightarrow 4{{\left| z \right|}^{2}}+6P+9{{\left| w \right|}^{2}}=36$ $\left( 2 \right)$.
$\left| z+4w \right|=7$$\Leftrightarrow \left( z+4w \right).\left( \overline{z}+4\overline{w} \right)=49$$\Leftrightarrow {{\left| z \right|}^{2}}+4P+16{{\left| w \right|}^{2}}=49$ $\left( 3 \right)$. Giải hệ phương trình gồm $\left( 1 \right)$, $\left( 2 \right)$, $\left( 3 \right)$ ta có:
$\left\{ \begin{array}{l} {\left| z \right|^2} = 33\\ P = – 28\\ {\left| w \right|^2} = 8 \end{array} \right.$$\Rightarrow P=-28$
Câu 4. Cho các số phức${{z}_{1}},{{z}_{2}},{{z}_{3}}$ thoả mãn $\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|=\left| {{z}_{3}} \right|=1$và ${{z}_{1}}^{3}+{{z}_{2}}^{3}+{{z}_{3}}^{3}+{{z}_{1}}{{z}_{2}}{{z}_{3}}=0$. Đặt $z={{z}_{1}}+{{z}_{2}}+{{z}_{3}}$, giá trị của ${{\left| z \right|}^{3}}-3{{\left| z \right|}^{2}}$ bằng:
A. $\left\{ -2;\,2 \right\}$. B. $\left\{ -2;\,-4 \right\}$. C. $\left\{ -4;4 \right\}$. D. $\left\{ 2;\,4 \right\}$.
Lời giải
Chọn B
Ta có $\left| {{z}_{1}} \right|=\left| {{z}_{2}} \right|=\left| {{z}_{3}} \right|=1\Rightarrow {{\overline{z}}_{1}}=\frac{1}{{{z}_{1}}};{{\overline{z}}_{2}}=\frac{1}{{{z}_{2}}};{{\overline{z}}_{3}}=\frac{1}{{{z}_{3}}}$ và đặt $\left| z \right|=x$
${{\left| z \right|}^{2}}={{\left| {{z}_{1}}+{{z}_{2}}+{{z}_{3}} \right|}^{2}}=\left( {{z}_{1}}+{{z}_{2}}+{{z}_{3}} \right)\left( \overline{{{z}_{1}}}+\overline{{{z}_{2}}}+\overline{{{z}_{3}}} \right)=3+{{z}_{1}}\left( \overline{{{z}_{2}}}+\overline{{{z}_{3}}} \right)+{{z}_{2}}\left( \overline{{{z}_{1}}}+\overline{{{z}_{3}}} \right)+{{z}_{3}}\left( \overline{{{z}_{1}}}+\overline{{{z}_{2}}} \right)$
$=3+\frac{{{z}_{1}}}{{{z}_{2}}}+\frac{{{z}_{2}}}{{{z}_{1}}}+\frac{{{z}_{1}}}{{{z}_{3}}}+\frac{{{z}_{3}}}{{{z}_{1}}}+\frac{{{z}_{3}}}{{{z}_{2}}}+\frac{{{z}_{2}}}{{{z}_{3}}}$
$=3+\frac{{{z}_{1}}^{2}\left( {{z}_{2}}+{{z}_{3}} \right)+{{z}_{2}}^{2}\left( {{z}_{1}}+{{z}_{3}} \right)+{{z}_{3}}^{2}\left( {{z}_{1}}+{{z}_{2}} \right)}{{{z}_{1}}{{z}_{2}}{{z}_{3}}}$
$=3+\frac{z\left( {{z}_{1}}^{2}+{{z}_{2}}^{2}+{{z}_{3}}^{2} \right)-{{z}_{1}}^{3}-{{z}_{2}}^{3}-{{z}_{3}}^{3}}{{{z}_{1}}{{z}_{2}}{{z}_{3}}}$
$=4+z\frac{{{\left( {{z}_{1}}+{{z}_{2}}+{{z}_{3}} \right)}^{2}}-2\left( {{z}_{1}}{{z}_{2}}+{{z}_{1}}{{z}_{2}}+{{z}_{2}}{{z}_{3}} \right)}{{{z}_{1}}{{z}_{2}}{{z}_{3}}}$
$=4+\frac{{{z}^{3}}}{{{z}_{1}}{{z}_{2}}{{z}_{3}}}-2z\left( \frac{1}{{{z}_{1}}}+\frac{1}{{{z}_{2}}}+\frac{1}{{{z}_{3}}} \right)$
$=4+\frac{{{z}^{3}}}{{{z}_{1}}{{z}_{2}}{{z}_{3}}}-2z\left( \overline{{{z}_{1}}}+\overline{{{z}_{2}}}+\overline{{{z}_{3}}} \right)$
$=4+\frac{{{z}^{3}}}{{{z}_{1}}{{z}_{2}}{{z}_{3}}}-2{{x}^{2}}\Rightarrow \left| 3{{x}^{2}}-4 \right|={{x}^{3}}$.
$ \Leftrightarrow \left[ \begin{array}{l} x = 1 \Rightarrow \left| z \right| = 1 \Rightarrow {\left| z \right|^3} – 3{\left| z \right|^2} = – 2\\ x = 2 \Rightarrow \left| z \right| = 2 \Rightarrow {\left| z \right|^3} – 3{\left| z \right|^2} = – 4 \end{array} \right.$Câu 5. Xét số phức $z$ thỏa mãn $\left( 1+2i \right)\left| z \right|=\frac{\sqrt{10}}{z}-2+i.$ Mệnh đề nào dưới đây đúng?
A. $\frac{3}{2}<\left| z \right|<2.$ B. $\left| z \right|>2.$ C. $\left| z \right|<\frac{1}{2}.$ D. $\frac{1}{2}<\left| z \right|<\frac{3}{2}.$
Lời giải:
Chọn D
Ta có ${{z}^{-1}}=\frac{1}{{{\left| z \right|}^{2}}}\overline{z}.$
Vậy $\left( 1+2i \right)\left| z \right|=\frac{\sqrt{10}}{z}-2+i$$\Leftrightarrow \left( \left| z \right|+2 \right)+\left( 2\left| z \right|-1 \right)i=\left( \frac{\sqrt{10}}{{{\left| z \right|}^{2}}} \right).\overline{z}$
$\Rightarrow \left| \left( \left| z \right|+2 \right)+\left( 2\left| z \right|-1 \right)i \right|=\left| \left( \frac{\sqrt{10}}{{{\left| z \right|}^{2}}} \right).\overline{z} \right|$
$\Rightarrow {{\left( \left| z \right|+2 \right)}^{2}}+{{\left( 2\left| z \right|-1 \right)}^{2}}=\left( \frac{10}{{{\left| z \right|}^{4}}} \right).{{\left| z \right|}^{2}}=\frac{10}{{{\left| z \right|}^{2}}}.$
Đặt $\left| z \right|=a>0.$ $\Rightarrow {{\left( a+2 \right)}^{2}}+{{\left( 2a-1 \right)}^{2}}=\left( \frac{10}{{{a}^{2}}} \right)\Leftrightarrow {{a}^{4}}+{{a}^{2}}-2=0$
$ \Leftrightarrow \left[ \begin{array}{l} {a^2} = 1\\ {a^2} = – 2 \end{array} \right.$$\Rightarrow a=1\Rightarrow \left| z \right|=1.$
Câu 6. Có bao nhiêu số phức $z$ thỏa mãn $\left| z \right|\left( z-4-i \right)+2i=\left( 5-i \right)z$?
A. $2$ B. $3$ C. $1$ D. $4$
Lời giải:
Chọn B
Ta có $\left| z \right|\left( z-4-i \right)+2i=\left( 5-i \right)z$
$\Leftrightarrow \left| z \right|z-4\left| z \right|-\left| z \right|i+2i=\left( 5-i \right)z$ $\Leftrightarrow z\left( \left| z \right|-5+i \right)=4\left| z \right|+\left( \left| z \right|-2 \right)i$.
Lấy module 2 vế ta được
$\left| z \right|\sqrt{{{\left( \left| z \right|-5 \right)}^{2}}+1}=\sqrt{{{\left( 4\left| z \right| \right)}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}}\Leftrightarrow {{\left| z \right|}^{2}}\left[ {{\left( \left| z \right|-5 \right)}^{2}}+1 \right]={{\left( 4\left| z \right| \right)}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}\left( 1 \right)$.
Đặt $t=\left| z \right|$, $t\ge 0$.
Phương trình $\left( 1 \right)$ trở thành
${{t}^{2}}\left[ {{\left( t-5 \right)}^{2}}+1 \right]={{\left( 4t \right)}^{2}}+{{\left( t-2 \right)}^{2}}$$\Leftrightarrow {{t}^{2}}\left( {{t}^{2}}-10t+26 \right)=17{{t}^{2}}-4t+4$
$\Leftrightarrow {{t}^{4}}-10{{t}^{3}}+9{{t}^{2}}+4t-4=0$ $\Leftrightarrow \left( t-1 \right)\left( {{t}^{3}}-9{{t}^{2}}+4 \right)=0$
$ \Leftrightarrow \left[ \begin{array}{l} t = 1\\ {t^3} – 9{t^2} + 4 = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} t = 1 & & \left( n \right)\\ t \approx 8,95 & \left( n \right)\\ t \approx 0,69 & \left( n \right)\\ t \approx – 0,64 & \left( l \right) \end{array} \right.$Ứng với mỗi giá trị $t\ge 0$, với $z=\frac{-4t+\left( 2-t \right)i}{5-i-t}$ suy ra có 3 số phức $z$ thỏa mãn.
Câu 7. Có bao nhiêu số phức thỏa mãn $\left| z \right|\left( z-6-i \right)+2i=\left( 7-i \right)z$?
A. $2$ B. $3$ C. $1$ D. $4$
Lời giải:
Chọn B
Đặt $\left| z \right|=a\ge 0,a\in \mathbb{R}$, khi đó ta có
$\left| z \right|\left( z-6-i \right)+2i=\left( 7-i \right)z$$\Leftrightarrow a\left( z-6-i \right)+2i=\left( 7-i \right)z$$\Leftrightarrow \left( a-7+i \right)z=6a+ai-2i$$\Leftrightarrow \left( a-7+i \right)z=6a+\left( a-2 \right)i$$\Leftrightarrow \left| \left( a-7+i \right) \right|\left| z \right|=\left| 6a+\left( a-2 \right)i \right|$ $\Leftrightarrow \left[ {{\left( a-7 \right)}^{2}}+1 \right]{{a}^{2}}=36{{a}^{2}}+{{\left( a-2 \right)}^{2}}$$\Leftrightarrow {{a}^{4}}-14{{a}^{3}}+13{{a}^{2}}+4a-4=0$
$ \Leftrightarrow \left( {a – 1} \right)\left( {{a^3} – 13{a^2} + 4} \right) = 0$
$ \Leftrightarrow \left[ \begin{array}{l} a = 1\\ {a^3} – 13{a^2} + 4 = 0 \end{array} \right.$Xét hàm số $f\left( a \right)={{a}^{3}}-13{{a}^{2}}+4\left( a\ge 0 \right)$, có bảng biến thiên là
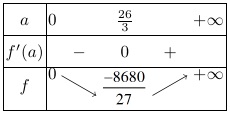
Đường thẳng $y=-4$ cắt đồ thị hàm số $f\left( a \right)$ tại hai điểm nên phương trình ${{a}^{3}}-13{{a}^{2}}+4=0$ có hai nghiệm khác $1$ (do $f\left( 1 \right)\ne 0$). Mỗi giá trị của $a$ cho ta một số phức $z$.
Vậy có $3$ số phức thỏa mãn điều kiện.
Câu 8. Có bao nhiêu số phức $z$ thỏa mãn $\left| z \right|\left( z-3-i \right)+2i=\left( 4-i \right)z$?
A. $1$ B. $3$ C. $2$ D. $4$
Lời giải:
Chọn B
$\left| z \right|\left( z-3-i \right)+2i=\left( 4-i \right)z$$\Leftrightarrow \left( \left| z \right|-4+i \right)z=3\left| z \right|+\left( \left| z \right|-2 \right)i$ (*)
$\Rightarrow \sqrt{{{\left( \left| z \right|-4 \right)}^{2}}+1}.\left| z \right|=\sqrt{9{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}}$ (1). Đặt $m=\left| z \right|\ge 0$ ta có $\left( 1 \right)\Leftrightarrow \left( {{\left( m-4 \right)}^{2}}+1 \right).{{m}^{2}}=9{{m}^{2}}+{{\left( m-2 \right)}^{2}}$$\Leftrightarrow {{m}^{4}}-8{{m}^{3}}+7{{m}^{2}}+4m-4=0$$\Leftrightarrow \left( m-1 \right)\left( {{m}^{3}}-7{{m}^{2}}+4 \right)=0$
$ \Leftrightarrow \left[ \begin{array}{l} m = 1\\ {m^3} – 7{m^2} + 4 = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} m = 1\\ m \approx 6,91638\\ m \approx 0.80344\\ m \approx – 0.71982 & \left( {\rm{L}} \right) \end{array} \right.$Từ (*) ta suy ra ứng với mỗi $\left| z \right|=m$ sẽ có một số phức $z=\frac{3m+\left( m-2 \right)i}{m-4+i}$ thỏa mãn đề bài.
Vậy có $3$ số phức $z$ thỏa mãn yêu cầu bài toán.
Câu 9. Có bao nhiêu số phức $z$ thỏa $\left| z+1-2i \right|=\left| \overline{z}+3+4i \right|$ và $\frac{z-2i}{\overline{z}+i}$
là một số thuần ảo ?
A. 0. B. Vô số. C. 1. D. 2.
Lời giải:
Chọn C
Đặt $z=x+yi\,(x,y\in \mathbb{R})$
Theo bài ra ta có
$\left| {x + 1 + \left( {y – 2} \right)i} \right| = \left| {x + 3 + \left( {4 – y} \right)i} \right|$ $ \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y – 2} \right)^2} = {\left( {x + 3} \right)^2} + {\left( {y – 4} \right)^2} \Leftrightarrow y = x + 5$Số phức
$\text{w}=\frac{z-2i}{\overline{z}+i}=\frac{x+\left( y-2 \right)i}{x+\left( 1-y \right)i}=\frac{{{x}^{2}}-\left( y-2 \right)\left( y-1 \right)+x\left( 2y-3 \right)i}{{{x}^{2}}+{{\left( y-1 \right)}^{2}}}$
$w$ là một số ảo khi và chỉ khi
$\left\{ \begin{array}{l} {x^2} – \left( {y – 2} \right)\left( {y – 1} \right) = 0\\ {x^2} + {\left( {y – 1} \right)^2} > 0\\ y = x + 5 \end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l} x = – \frac{{12}}{7}\\ y = \frac{{23}}{7} \end{array} \right.$Vậy $z=-\frac{12}{7}+\frac{23}{7}i$.Vậy chỉ có $1$ số phức $z$ thỏa mãn.
Câu 10. Có bao nhiêu số phức $z$ thỏa mãn $\left| z \right|\left( z-5-i \right)+2i=\left( 6-i \right)z$?
A. $1$ B. $3$ C. $4$ D. $2$
Lời giải:
Chọn B
Ta có $\left| z \right|\left( z-5-i \right)+2i$$=\left( 6-i \right)z$$\Leftrightarrow \left( \left| z \right|-6+i \right)z$$=5\left| z \right|+\left( \left| z \right|-2 \right)i$ $\left( 1 \right)$
Lây môđun hai vế của $\left( 1 \right)$ ta có:
$\sqrt{{{\left( \left| z \right|-6 \right)}^{2}}+1}.\left| z \right|$$=\sqrt{25{{\left| z \right|}^{2}}+{{\left( \left| z \right|-2 \right)}^{2}}}$
Bình phương và rút gọn ta được:
${{\left| z \right|}^{4}}-12{{\left| z \right|}^{3}}+11{{\left| z \right|}^{2}}+4\left| z \right|-4=0$$\Leftrightarrow \left( \left| z \right|-1 \right)\left( {{\left| z \right|}^{3}}-11{{\left| z \right|}^{2}}+4 \right)=0$
$ \Leftrightarrow \left[ \begin{array}{l} \left| z \right| = 1\\ {\left| z \right|^3} – 11{\left| z \right|^2} + 4 = 0 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} \left| z \right| = 1\\ \left| z \right| = 10,9667…\\ \left| z \right| = 0,62…\\ \left| z \right| = – 0,587… \end{array} \right.$Do $\left| z \right|\ge 0$, nên ta có $\left| z \right|=1$, $\left| z \right|=10,9667…$, $\left| z \right|=0,62…$. Thay vào $\left( 1 \right)$ ta có $3$ số phức thỏa.
————————-




0 Bình luận