Khoảng đồng biến nghịch -biến của hàm số

Lý thuyết hàm số: Khoảng đồng biến nghịch-biến của hàm số

Định nghĩa: Cho \(f(x)\) là hàm số xác định trên K, K là một khoảng, một đoạn hoặc một nửa khoảng.

 • Hàm số \(f(x)\) gọi là đồng biến (hay tăng) trên K nếu ∀\(x_1,x_2\in K,\), \(x_1\) < \(x_2\) ⇒ \(f\left(x_1\right)\) < \(f\left(x_2\right)\)

• Hàm số \(f(x)\) gọi là nghịch biến (hay giảm) trên K nếu ∀\(x_1,x_2\in K,\),  \(x_1\) < \(x_2\) ⇒ \(f\left(x_1\right)\) > \(f\left(x_2\right)\)

     + Nếu một hàm số đồng biến trên K thì trên đó, đồ thị của nó đi từ phía dưới bên trái lên phía trên bên phải ;

     + Nếu một hàm số nghịch biến trên K thì trên đó, đồ thị của nó đi từ phía trên bên trái xuống phía dưới bên phải.

Định lý: Cho hàm số y = \(f\left(x\right)\) có đạo hàm y’  $\forall x \in D$.

• Nếu \(f’\left(x\right)\) ≥ 0, ∀x ∈ D và \(f’\left(x\right)\)= 0 tại hữu hạn điểm thuộc D thì y = \(f\left(x\right)\) đồng biến trên D;

• Nếu \(f’\left(x\right)\) ≤ 0, ∀x ∈ D và \(f’\left(x\right)\)= 0 tại hữu hạn điểm thuộc D thì y = \(f\left(x\right)\) nghịch biến trên D;

• Nếu \(f’\left(x\right)\) = 0, ∀x ∈ D thì y = \(f\left(x\right)\) không đổi (hàm số hằng) trên D.

B. Kỹ Năng Cơ Bản

• Tìm tập xác định.
• Tính y’. Tìm các điểm tại đó y’ bằng 0 hoặc không xác định.
• Tính các giới hạn (nếu cần): $\mathop {\lim }\limits_{x \to \pm \infty } f(x);\mathop {\lim }\limits_{x \to {{({x_0})}^ \pm }} f(x)$.
•  Lập bảng biến thiên.
• Tìm giá trị lớn nhất- nhỏ nhất của hàm số.

C. Các dạng toán cơ bản

Dạng 1. Tìm các khoảng đơn điệu của hàm số.

Quy tắc:

• Tìm tập xác định \(D_f\) .
• Tính y’. Tìm các điểm tại đó y’ bằng 0 hoặc không xác định.
• Tính các giới hạn (nếu cần): $\mathop {\lim }\limits_{x \to \pm \infty } f(x);\mathop {\lim }\limits_{x \to {{({x_0})}^ \pm }} f(x)$.
• Lập bảng biến thiên.
• Kết luận về khoảng  đồng biến- nghịch biến.

Ví dụ 1 : Xét tính đơn điệu của hàm số :

\(y=\frac{x^3}{3}-x^2-3x+2\)

Bài giải :

Tập xác định : \(D=R\)

Ta có : \(y’=x^2-2x-3,y’=0\Leftrightarrow x^2-2x-3=0\Leftrightarrow x=-1;x=3\)

Lập bảng biến thiên :

Kết luận: Hàm số đồng biến trên mỗi khoảng \(\left(-\infty;-1\right)\) và \(\left(3;+\infty\right)\), nghịch biến trên \(\left(-1;3\right)\)

Dạng 2. Chứng minh hàm số đồng biến (hoặc nghịch biến) trên khoảng D.

Quy tắc:

+ Tìm y’.

+ CMR: \(f’\left(x\right)\) ≥ 0, ∀x ∈ D (hoặc  \(f’\left(x\right)\) ≤ 0, ∀x ∈ D). Suy ra điều phải CM.

Ví dụ 2 : Chứng minh rằng hàm số \(f\left(x\right)=x+\cos^2x\) đồng biến trên R

Bài giải :

Tập xác định \(D=R\)

Ta có: $f’\left( x \right) = 1 – \sin 2x = {(sinx + \cos x)^2} \ge 0;\forall x \in R$. Vậy ta có điều phải CM.

Dạng 3. Tìm điều kiện tham số để hàm số Đồng biến (hoặc Nghịch biến) trên D.

Quy tắc:

• Tính y’.

+ Hàm số đồng biến trên D <=>\(f’\left(x\right)\) ≥ 0, ∀x ∈ D <=>$f(x) \ge m;\forall x \in D$$ \Leftrightarrow \mathop {Min}\limits_D f(x) \ge m$.

+ Hàm số nghịch biến trên D <=>\(f’\left(x\right)\) ≤ 0, ∀x ∈ D<=>$f(x) \le m;\forall x \in D$$\mathop {Max}\limits_D f(x) \le m$

Ví dụ 3 : Tìm m để hàm số : \(y=x^3-3mx^2+3\left(2m+3\right)x+1\) nghịch biến trong khoảng \(\left(-\frac{1}{2};\frac{1}{2}\right)\)

Bài giải :

Tập xác định R

Ta có \(y’=3x^2-6mx+3\left(2m-1\right)=3\left[x^2-2mx+\left(2m+3\right)\right]\)

Hàm số nghịch biến trong khoảng \(\left(-\frac{1}{2};\frac{1}{2}\right)\) khi và chỉ khi \(y’\le0\), mọi \(x\in\left(-\frac{1}{2};\frac{1}{2}\right)\)

hay \(f\left(x\right)=x^2-2mx+\left(2m+3\right)\le0\left(1\right)\)mọi \(x\in\left(-\frac{1}{2};\frac{1}{2}\right)\)

Ta có (1) \(\Leftrightarrow2m\left(x-1\right)\ge x^2+3\Leftrightarrow m\le\frac{x^2+3}{2x-2}\) với mọi \(x\in\left(-\frac{1}{2};\frac{1}{2}\right)\)

Xét hàm số \(g\left(x\right)=\frac{x^2+3}{2x-2}\); với mọi \(x\in\left(-\frac{1}{2};\frac{1}{2}\right)\)

\(g’\left(x\right)=\frac{2x\left(2x-2\right)-2\left(x^2+3\right)}{\left(2x-2\right)^2}=\frac{\left(x+1\right)\left(2x-6\right)}{\left(2x-2\right)^2}<0\) với mọi \(x\in\left(-\frac{1}{2};\frac{1}{2}\right)\)

Bảng biến thiên :

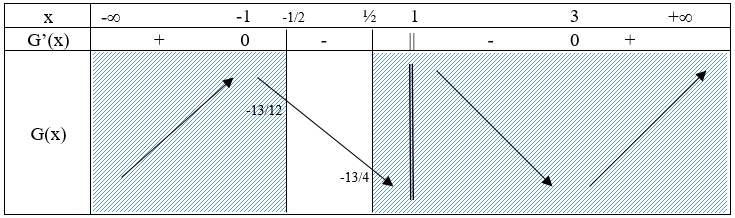
Từ bảng biến thiên suy ra: $\mathop {Min}\limits_{\left( { – \frac{1}{2};\frac{1}{2}} \right)} f(x) = – \frac{{13}}{4}$.

Vậy: \(m\le-\frac{13}{4}\) là giá trị cần tìm

Cách khác.

+ Dễ thấy nếu \(f\left(x\right)=0\) vô nghiệm hoặc có nghiệm kép thì \(f\left(x\right)\ge0\) với mọi x, khi đó không có giá trị nào m thỏa mãn

+ Phương trình \(f\left(x\right)=0\) có hai nghiệm phân biệt \(x_1,x_2\)

\(x_1,x_2,\) (\(x_1\)<\(x_2\))\(\Leftrightarrow\Delta’>0\Leftrightarrow m^2-2m-2>0\) \(\Leftrightarrow m>3\) hoặc \(m<-1\)

Khi đó \(f\left(x\right)\le0\), với mọi \(x\in\left(-\frac{1}{2};\frac{1}{2}\right)\)\(\Leftrightarrow\left(-\frac{1}{2};\frac{1}{2}\right)\subset\left[x_1;x_2\right]\Leftrightarrow x_1\le-\frac{1}{2}\)<\(\frac{1}{2}\le x_2\)