Ý nghĩa của đạo hàm

Ý NGHĨA CỦA ĐÀO HÀM

I. Mối liên hệ giữa đạo hàm và tính liên tục của hàm số

1.1. Định lý

• Nếu hàm số $y=f(x)$ có đạo hàm tại x₀ thì nó liên tục tại điểm đó.

• Chiều ngược lại chưa chắc đúng.

1.2. Chứng minh

Chiều thuận: Hàm số có đạo hàm tại x₀ thì liên tục tại x₀ .

Theo giả thiết hàm số có đạo hàm tại x₀ suy ra: $f'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} \left( {\frac{{\Delta y}}{{\Delta x}}} \right)$.

$\mathop {\lim }\limits_{\Delta x \to 0} \Delta y = \mathop {\lim }\limits_{\Delta x \to 0} \left( {\frac{{\Delta y}}{{\Delta x}}.\Delta x} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \left( {\frac{{\Delta y}}{{\Delta x}}} \right)\mathop {\lim }\limits_{\Delta x \to 0} \left( {\Delta x} \right) = f’\left( x \right).0 = 0$

Mặt khác: $\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} f(x) = 0 = f(0)$. Vậy hàm số liên tục tại x₀ .

Chiều ngược lại: Hàm số liên tục tại x₀ nhưng chưa chắc có đạo hàm tại x₀ .

Ví dụ minh họa

Chứng minh rằng hàm số:

$f(x) = \left\{ {\begin{array}{*{20}{c}} {{-x^2}}\\ { x} \end{array}} \right.\begin{array}{*{20}{c}} ;\\ ; \end{array}\begin{array}{*{20}{c}} {x \ge 0}\\ {x < 0} \end{array}$

liên tục tại x=0 nhưng không có đạo hàm tại x=0.

Giải

a).$\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \left( { – {x^2}} \right) = 0 = f(0)$. Suy ra hàm số liên tục bên phải tại x=0.

$\mathop {\lim }\limits_{x \to {0^ – }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} \left( x \right) = 0 = f(0)$. Suy ra hàm số liên tục bên trái tại x=0.

Vậy hàm số liên tục tại x=0.

b). $f'({0^ + }) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{f(x) – f(0)}}{{x – 0}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{ – {x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \left( { – x} \right) = 0$

$f'({0^ – }) = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{f(x) – f(0)}}{{x – 0}} = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{ – x}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \left( { – 1} \right) = – 1$

Do: $f'({0^ + }) = 0 \ne f'({0^ – }) = – 1$ nên hàm số không có đạo hàm tại điểm x=0.

Vậy ta có điều phải chứng minh.

Chú ý: Hàm số liên tục tại x₀ nhưng không có đạo hàm tại điểm x₀ thì đồ thị bị gãy tại điểm x₀ .

II. Ý nghĩa hình học của đạo hàm

2.1. Tiếp tuyến của đường cong phẳng

Trên mặt phẳng 0xy, cho hàm số: $y = f(x)$ có đồ thị (C). Giả sử M₀ (x₀ ;f(x₀)) $ \in $ (C).

Một cát tuyến M₀t chuyển động quanh M₀ cắt (C) tại M(x;y). Giả sử M₀T là vị trí giới hạn của M₀t. Khi đó, M₀T gọi là tiếp tuyến của (C) tại điểm x₀ . Điểm x₀ gọi là tiếp điểm.

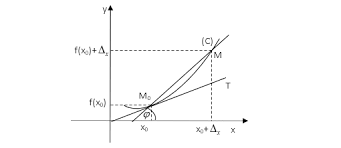
2.2. Ý nghĩa hình học của đạo hàm

Cho hàm số $y = f(x)$ xác định trên khoảng (a;b) và có đạo hàm tại ${x_0} \in (a;b)$. Gọi (C) là đồ thị của hàm số.

Định lí

Đạo hàm của hàm số $y = f(x)$ tại điểm x₀ là hệ số góc của tiếp tuyến M₀T của (C) tại điểm M₀ (x₀; f(x₀)).

2.3. Phương trình tiếp tuyến

Định lí

Phương trình tiếp tuyến của đồ thị (C) của hàm số $y = f(x)$ tại điểm ${M_0}\left( {{x_0};f({x_0})} \right)$ là:

$y – {y_0} = f\left( {{x_0}} \right)\left( {x – {x_0}} \right)$

trong đó: ${y_0} = f\left( {{x_0}} \right)$.

Ví dụ minh họa

Cho hàm số: $y = {x^2}$ có đồ thi (C), lập phương trình tiếp tuyến của (C) tại điểm x₀=2.

Giải

$y’\left( 2 \right) = \mathop {\lim }\limits_{x \to 2} \frac{{f(x) – f(2)}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} – {2^2}}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x – 2} \right)\left( {x + 2} \right)}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 2} \right) = 4$.

${y_0} = f(2) = {2^2} = 4$

Phương trình tiếp tuyến: $y – 4 = 4(x – 2) \Leftrightarrow y = 4x – 4$.

III. Ý nghĩa vật lý của đạo hàm

3.1. Vận tốc tức thời của chất điểm

Một chất điểm M chuyển động trên trục s’Os. Quãng đường chuyển động của chất điểm M là một hàm số của thời gian t: s=s(t). trong khoảng thời gian từ t₀ đến t₁ , chất điểm đi được quãng đường là: s-s₀ =s(t)-s(t₀).

• Nếu chất điểm chuyển động đều thì tỉ số: $\frac{{s – {s_0}}}{{t – {t_0}}} = \frac{{s(t) – s({t_0})}}{{t – {t_0}}}$ là hằng số với mọi t. Đại lượng đó là vận tốc của chuyển động tại mọi thời điểm.
• Nếu chất điểm chuyển động không đều thì đại lượng đó là vận tốc trung bình của chuyển động trong khoảng thời gian |t-t₀|.
• Nếu t càng gần tới t₀ tức là |t-t₀| càng nhỏ thì vận tốc trung bình càng thể hiện được chính xác hơn độ nhanh chậm của chuyển động tại thời điểm t₀. Khi đó: $\mathop {\lim }\limits_{t – {t_0}} \frac{{s(t) – s({t_0})}}{{t – {t_0}}}$ được gọi là vận tốc tức thời của chuyển động tại thời điểm t₀.

Hệ quả: $v({t_0})=s'({t_0}) = \mathop {\lim }\limits_{t – {t_0}} \frac{{s(t) – s({t_0})}}{{t – {t_0}}}$.

Ví dụ: Một vật rơi tự do theo phương trình: $s = \frac{1}{2}g{t^2}$, trong đó $g \approx 9,8m/{s^2}$ là gia tốc trọng trường. Tính vận tốc tức thời của chuyển động tại thời điểm t=5s.

Giải

Vận tốc tức thời của chuyển động là:

$v(5)=s'(5) = \mathop {\lim }\limits_{t \to 5} \frac{{s(t) – s(5)}}{{t – 5}} = \mathop {\lim }\limits_{t \to 5} \frac{{\frac{1}{2}g{t^2} – \frac{1}{2}g{{.5}^2}}}{{t – 5}} = \frac{1}{2}g\mathop {\lim }\limits_{t \to 5} \left( {t + 5} \right) = 10g \approx 98\left( {m/s} \right)$.

3.2. Gia tốc tức thời của một chuyển động

Xét chuyển động xác định bởi phương trình $s=f(t)$, Vận tốc tức thời tại thời điểm $t$ của chuyển động là $v(t)=f'(t)$.

Lấy số gia $\Delta t$ tại $t$ thì $v(t)$ có số gia tương ứng là $\Delta v$.

Khi đó: $v'(t)= \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta v}}{{\Delta t}}$ là gia tốc tức thời của của chuyển động tại thời điểm $t$. Kí hiệu là $a(t)$.

Hệ quả

$a(t) = v'(t) = s”(t)$

Ví dụ

Gia tốc tức thời của rơi tự do: $s(t) = \frac{1}{2}g{t^2};g \approx 9,8\left( {m/s} \right)$ tại thời điểm t=3 s bằng bao nhiêu?

Giải

Ta có: $v(t)=s'(t) = \left( {\frac{1}{2}g{t^2}} \right)’ = gt$

$a(t) = s”(t) = \left( {gt} \right)’ = g$= Hằng số với mọi $t$.

Vậy: Gia tốc của vật rơi tự do luôn bằng $g \approx 9,8\left( {m/{s^2}} \right)$.

3.3. Cường độ tức thời của dòng điện qua một tiết diện phẳng

Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t: Q=Q(t). Cường độ trung bình bình của dòng điện trong khoảng thời gian |t-t₀| là: $I = \frac{{Q(t) – Q({t_0})}}{{t – {t_0}}}$. Nếu |t-t₀| càng nhỏ thì tỉ số này càng biểu thị chính xác hơn cường độ dòng điện tại thời điểm t₀. Khi đó đại lượng: $I = \mathop {\lim }\limits_{t \to {t_0}} \frac{{Q(t) – Q({t_0})}}{{t – {t_0}}}$ gọi là cường độ tức thời của dòng điện tại thời điểm t₀.

Hệ quả: $I({t_0})=Q'({t_0}) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{Q(t) – Q({t_0})}}{{t – {t_0}}}$.

BÀI TẬP LUYỆN TẬP

Câu 1: Số gia của hàm số f(x)=x^3, ứng với: x_0=2 và ∆_x=1 là:
A. 19

B. -7

C. 7

D. 0

Câu 2: Số gia của hàm số $f(x)=x^2-1$ theo và $∆_x$ là:
A. $2x+∆_x$

B. $∆_x (x+∆_x)$

C. $∆_x (2x+∆_x)$

D. $(2x∆)_x$

Câu 3: Số gia của hàm số $f(x) = \frac{{{x^2}}}{2}$ ứng với số gia $∆_x$ của đối số tại $x_0=-1$ là:

A. $1/2 (∆_x )^2+∆_x$

B. $1/2 (∆_x )^2-∆_x$

C. $1/2 ((∆_x )^2-∆_x ) $

D. $1/2 (∆_x )^2-∆_x+1$

Câu 4: Hệ số góc của tiếp tuyến với đồ thị hàm số $f(x)=-x^3$ tại điểm M(-2; 8) là:

A. 12

B. -12

C. 192

D. -192

Câu 5: Phương trình tiếp tuyến của Parabol $y=-3x^2+x-2$ tại điểm M(1; 1) là:

A. y=5x+6

B. y=-5x+6

C. y=-5x-6

D. y=5x-6

Câu 6: Một chất điểm chuyển động có phương trình $s=t^2$ (t tính bằng giây, s tính bằng mét). Vận tốc của chất điểm tại thời điểm $t_0=3$ (giây) bằng:

A. 2 m⁄s

B. 5 m⁄s

C. 6 m⁄s

D. 3 m⁄s

Câu 7: Điện lượng truyền trong dây dẫn có phương trình Q=5t+3 thì cường độ dòng điện tức thời tại điểm $t_0=3$ bằng:

A. 15(A)

B. 8(A)

C. 3(A)

D. 5(A)

Câu 8: Cho chuyển động thẳng xác định bởi phương trình , trong đó t được tính bằng giây và S được tính bằng mét. Vận tốc tại thời điểm gia tốc bị triệt tiêu là:

A. 3 m/s

B. −3 m/s

C. $\frac{1}{3}$ m/s

D. 1 m/s

Câu 9. Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu  (bỏ qua sức cản của không khí). Thời điểm tại đó tốc độ của viên đạn bằng 0 là:

A. 10s      

B. 20s        

C. 25s          

D. 30s          

Câu 10. Một vật chuyển động với phương trình $S(t) = 4{t^2} + {t^3}$, trong đó t>0, t tính bằng (s), S(t) tính bằng (m/s). Tìm gia tốc của vật tại thời điểm vận tốc của vật bằng 11.

A.  $11\left( {m/{s^2}} \right)$                

B.   $12\left( {m/{s^2}} \right)$            

C.  $13\left( {m/{s^2}} \right)$              

D. 14\left( {m/{s^2}} \right)$

—————————