Các quy tắc tính giới hạn hàm số

Các quy tắc tính giới hạn hàm số

1. Quy tắc giới hạn của tích \(f(x).g(x)\)

+ Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \pm \infty \) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = L \ne 0\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right).g\left( x \right)} \right]\) được cho trong bảng sau:

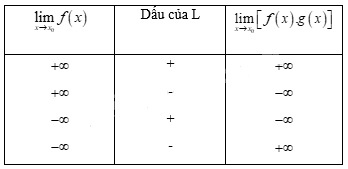
2. Quy tắc tìm giới hạn của thương \(\dfrac{f(x)}{g(x)}\)

+ Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L \ne 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\) và \(g\left( x \right) > 0\) hoặc \(g\left( x \right) < 0\) với mọi \(x \in J\backslash \left\{ {{x_0}} \right\}\), trong đó \(J\) là một khoảng nào đó chứa \({x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) được cho trong bảng sau:

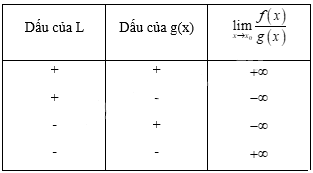
3. Cách tính giới hạn hàm số thường gặp

3.1.Dạng $\frac{0}{0}$ đối với giới hạn tại một điểm

Ví dụ 1: Tính: $\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 16}}{{x – 4}}$

Giải

Bước 1: Ta thế 4 vào phương trình f(x) thì sẽ được dạng  nên khẳng định đây là dạng $\frac{0}{0}$.

Bước 2: Biến đổi: $\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 16}}{{x – 4}}$ $ = \mathop {\lim }\limits_{x \to 4} \frac{{\left( {x – 4} \right)\left( {x + 4} \right)}}{{x – 4}}$ $ = \mathop {\lim }\limits_{x \to 4} \left( {x + 4} \right) = 8$

Ví dụ 2.

Tính $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 1} – 1}}{{{x^2}}}$

Giải

Bước 1: Ta thế 0 vào biểu thức dưới dấu lim thì sẽ thấy dạng  $\frac{0}{0}$  nên khẳng định đây là dạng  $\frac{0}{0}$.

Bước 2: Lúc này ta biến đổi nó bằng cách nhân lượng liên hợp cho cả tử và mẫu:

$\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 1} – 1}}{{{x^2}}}$ $ = \lim \frac{{\left( {\sqrt {{x^2} + 1} – 1} \right)\left( {\sqrt {{x^2} + 1} + 1} \right)}}{{{x^2}\left( {\sqrt {{x^2} + 1} + 1} \right)}}$ $\mathop { = \lim }\limits_{x \to 0} \frac{{{x^2}}}{{{x^2}\left( {\sqrt {{x^2} + 1} + 1} \right)}}$

Đến đây, chia cả tử và mẫu cho x² ta được: $ = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt {{x^2} + 1} + 1}} = \frac{1}{2}$

3.2.Dạng $\frac{\infty }{\infty }$

 Phương pháp: Ta chia cho x với số mũ lớn nhất của tử và mẫu.

Ví dụ 1.

Tính giới hạn sau: $\mathop {\lim }\limits_{x \to + \infty } \frac{{4{x^2} – x – 1}}{{3 + 2{x^2}}}$.

Giải

Thay $ + \infty $ và biểu thức ta thấy có dạng $\frac{{ + \infty }}{{ + \infty }}$.

Lại có bậc của x lớn nhất bằng 2, ta chia cả tử và mẫu cho x².

$\mathop {\lim }\limits_{x \to + \infty } \frac{{4{x^2} – x – 1}}{{3 + 2{x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{4 – \frac{1}{x} – \frac{1}{{{x^2}}}}}{{\frac{3}{{{x^2}}} + 2}} = \frac{4}{2} = 2$

3.3. Dạng ${ + \infty + \infty }$

Ví dụ

Tính các giới hạn sau: $\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$

Giải

$\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{\left| x \right|\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – x\sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{x\left( { – \sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} – 1} \right)}}{{x Ví dụ1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – \sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} – 1}}{{1 – \frac{1}{x}}} = \frac{{ – 2}}{1} = – 2$.

Lưu ý: Học sinh rất dễ nhầm dạng ${ + \infty + \infty }$ và dạng ${ + \infty – \infty }$.

3.4. Dạng ${ + \infty – \infty }$

Ví dụ

Tính gới hạn sau:$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right)$.

Giải

Bước 1: Nhân với biểu thức liên hợp của biểu thức sau dấu lim.

Bước 2: Sau liên hợp, có dạng $\frac{\infty }{\infty }$, nên ta chia cả tử và mẫu cho x.

$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right)$

$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right)\left( {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} } \right)}}{{\left( {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} } \right)}}$

$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – x – 1}}{{\left( {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} } \right)}}$

$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 1 – \frac{1}{x}}}{{\left( {\sqrt {1 – \frac{1}{x}} + \sqrt {1 + \frac{1}{{{x^2}}}} } \right)}} = – \frac{1}{2}$

3.5. Dạng ${0.\infty }$

Ví dụ

Tính giới hạn sau:$\mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\sqrt {\frac{x}{{{x^2} – 9}}} $

Giải

$\mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\sqrt {\frac{x}{{{x^2} – 9}}} $

$ = \mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\frac{{\sqrt x }}{{\sqrt {{x^2} – 9} }}$

$ = \mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\frac{{\sqrt x }}{{\sqrt {x – 3} .\sqrt {x + 3} }}$

$ = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{\sqrt {x – 3} \sqrt x }}{{\sqrt {x + 3} }} = 0$

Chúc các bạn thành công!

Xem thêm:

• Các phương pháp tính giới hạn dãy số.
• Các phương pháp tính gới hạn hàm số.