Tổng và hiệu của hai vectơ
1. Phép cộng hai véc tơ
1.1. Định nghĩa
Cho hai vectơ
và
. Lấy một điểm O tùy ý, vẽ
và
. Vectơ
được gọi là tổng của hai vectơ
và
. Ta kí hiệu tổng của hai vectơ
và
là
. Vậy
(hình vẽ).
Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.
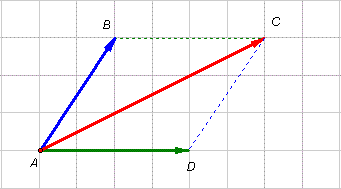
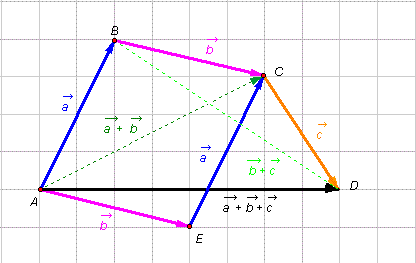
Với mọi hình bình hành ABCD ta luôn có: 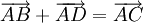 (hình vẽ).
(hình vẽ).
1.3. Tính chất của phép cộng các vectơ
Với ba vectơ 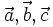 tùy ý ta có: tùy ý ta có: |
|
*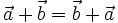 |
(tính chất giao hoán) |
| *$\left( {\vec a + \vec b} \right) + \vec c = \vec a + \left( {\vec b + \vec c} \right) = \vec a + \vec b + \vec c$ | (tính chất kết hợp) |
*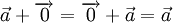 |
(tính chất của Vectơ-không). |
Chứng minh:(hình vẽ).
2. Hiệu của hai vectơ
2.1. Vectơ đối của một véc tơ
Cho vectơ
. vectơ có cùng độ dài và ngược hướng với
được gọi là vectơ đối của vectơ
, kí hiệu là
.
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của  là
là 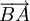 , nghĩa là
, nghĩa là 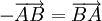 .
.
Đặc biệt, vectơ đối của vectơ  là vectơ
là vectơ  .
.
2.2. Phép trừ hai vec tơ
a) Định nghĩa hiệu của hai vectơ
Cho hai vectơ  và
và  . Ta gọi hiệu của hai vectơ
. Ta gọi hiệu của hai vectơ  và
và  là vectơ
là vectơ 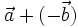 . Kí hiệu
. Kí hiệu 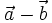 .
.
Hệ quả: 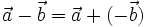
b) Quy tắc ba điểm đối với phép trừ
Với mọi ba điểm O;A;B ta luôn có: \(\overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {AB} \).

c) Quy tắc trung điểm
+ Với I là trung điểm AB, ta luôn có: $\overrightarrow {IA} + \overrightarrow {IB} = \vec 0$
d) Quy tắc trọng tâm tam giác
+ Với G là trọng tâm tam giác ABC, ta luôn có: 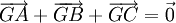 .
.
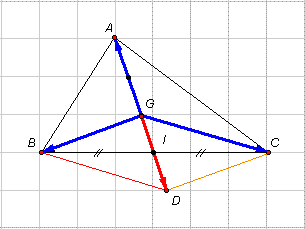
CHỨNG MINH
- Thuận
Gọi I là trung điểm của BC.
Vẽ D là điểm đối xứng với G qua I.
Từ (1)&(2) suy ra BGCD là hình bình hành.
Từ (3) suy ra 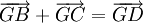
Từ (2) suy ra G là trung điểm của đoạn thẳng AD.
Từ (5) suy ra 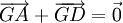 .
.
Từ (4)&(6), ta có: 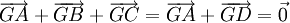 (đpcm).
(đpcm).
- Đảo
Ngược lại, giả sử 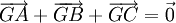 . Vẽ hình bình hành BGCD có I là giao điểm của hai đường chéo. Khi đó
. Vẽ hình bình hành BGCD có I là giao điểm của hai đường chéo. Khi đó 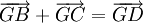 , suy ra
, suy ra 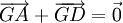 nên G là trung điểm của AD. Do đó ba điểm A, G, D thẳng hàng, GA = 2 GI, điểm G nằm giữa A và I. Vậy G là trọng tâm của tam giác ABC.
nên G là trung điểm của AD. Do đó ba điểm A, G, D thẳng hàng, GA = 2 GI, điểm G nằm giữa A và I. Vậy G là trọng tâm của tam giác ABC.
3. Các ví dụ minh họa
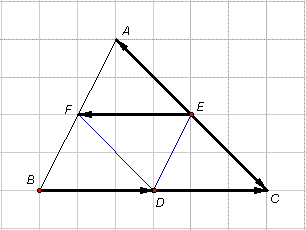
Ví dụ 1. Nếu D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC, khi đó ta có:
- Hai vectơ
 và
và  có cùng độ dài nhưng ngược hướng với nhau nên chúng là hai vectơ đối nhau. Do đó, ta có thể viết
có cùng độ dài nhưng ngược hướng với nhau nên chúng là hai vectơ đối nhau. Do đó, ta có thể viết
-
 hoặc
hoặc 
Tương tự, ta có:
 hoặc
hoặc 
 hoặc
hoặc
Ví dụ 2. Chứng minh rằng: “Với bốn điểm bất kì A, B, C, D ta luôn có:  “.
“.
Lời giải
Ta có:
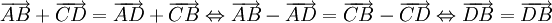 – luôn đúng.
– luôn đúng.
Vậy đẳng thức đã cho luôn đúng (đpcm).
Ví dụ 3. Cho hình vuông $ABCD$ có cạnh bằng $a$ với tâm là $O$. Tính:
a) Độ dài vectơ $\overrightarrow{OA}-\overrightarrow{CB}$
b) Tính $\left| \overrightarrow{AB}+\overrightarrow{DC} \right|$.
Lời giải
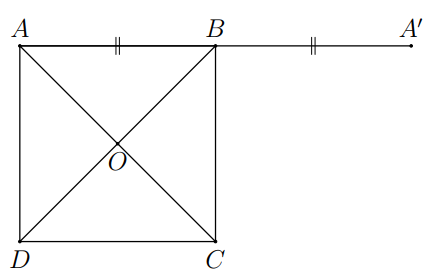
a) Ta có $\overrightarrow{OA}-\overrightarrow{CB}=\overrightarrow{CO}-\overrightarrow{CB}=\overrightarrow{BO}$.
Mặt khác $BO=\frac{1}{2}BD=\frac{1}{2}\sqrt{{{a}^{2}}+{{a}^{2}}}=\frac{a\sqrt{2}}{2}$.
Nên $\left| \overrightarrow{OA}-\overrightarrow{CB} \right|=\frac{a\sqrt{2}}{2}$.
b) Gọi ${A}’$ là điểm đối xứng với $A$ qua $B$.
Ta có $\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AB}+\overrightarrow{B{A}’}=\overrightarrow{A{A}’}$ nên $\left| \overrightarrow{AB}+\overrightarrow{DC} \right|=\left| \overrightarrow{A{A}’} \right|=2a$.
Ví dụ 4. Cho tam giác $ABC$. Gọi $M$, $N$, $P$ lần lượt là trung điểm của $BC$, $CA$, $AB$. Chứng minh rằng:
a) $\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}=\vec{0}$
b) $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}$, với $O$ là điểm bất kì.
Lời giải
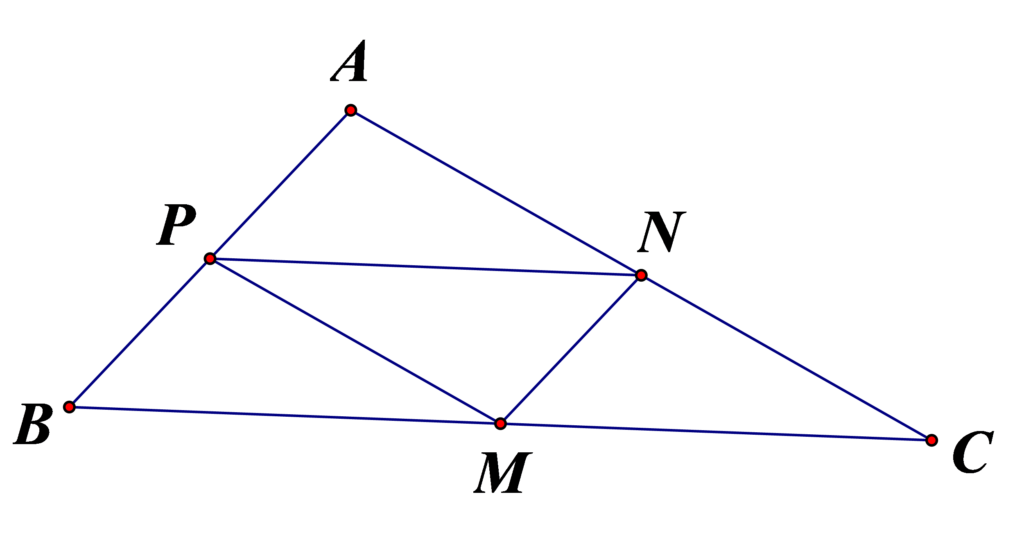
a) Vì $PN$, $MN$ là đường trung bình của tam giác $ABC$ nên $PN\,\text{//}\,BM$, $MN\,\text{//}\,BP$ suy ra tứ giác $BMNP$ là hình bình hành $\Rightarrow \overrightarrow{BM}=\overrightarrow{PN}$.
$N$ là trung điểm của $AC\Rightarrow \overrightarrow{CN}=\overrightarrow{NA}$.
Do đó theo quy tắc ba điểm ta có
$\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}=\left( \overrightarrow{PN}+\overrightarrow{NA} \right)+\overrightarrow{AP}$$=\overrightarrow{PA}+\overrightarrow{AP}=\vec{0}$.
b) Theo quy tắc ba điểm ta có
$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\left( \overrightarrow{OP}+\overrightarrow{PA} \right)+\left( \overrightarrow{OM}+\overrightarrow{MB} \right)+\left( \overrightarrow{ON}+\overrightarrow{NC} \right)$$=\left( \overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP} \right)+\overrightarrow{PA}+\overrightarrow{MB}+\overrightarrow{NC}$$=\left( \overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP} \right)-\left( \overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP} \right)$
Theo câu a) $\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}=\vec{0}$ ta suy ra $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}$.
Ví dụ 5. Cho tam giác $ABC$. Xác định điểm $M$ thỏa điều kiện $\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\vec{0}$.
Lời giải
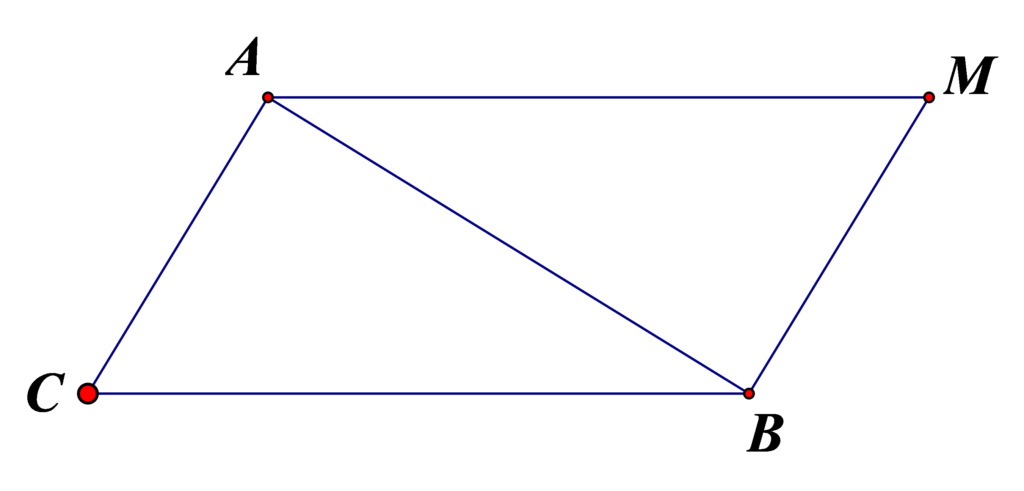
Ta có $\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\vec{0}$
$\Leftrightarrow \overrightarrow{MA}+\overrightarrow{CB}=\overrightarrow{0}$
$\Leftrightarrow \overrightarrow{MA}=\overrightarrow{BC}$.
Suy ra $M$ là đỉnh thứ tư của hình bình hành $ACBM$.
Ví dụ 6. Cho hình chữ nhật $ABCD$ có $AB=2$, $AD=1$. Gọi $I$ là trung điểm $CD$. Hãy tính:
a) $\left| \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BC} \right|$.
b) $\left| \overrightarrow{AC}-\overrightarrow{AB}-\overrightarrow{AI} \right|$.
Lời giải
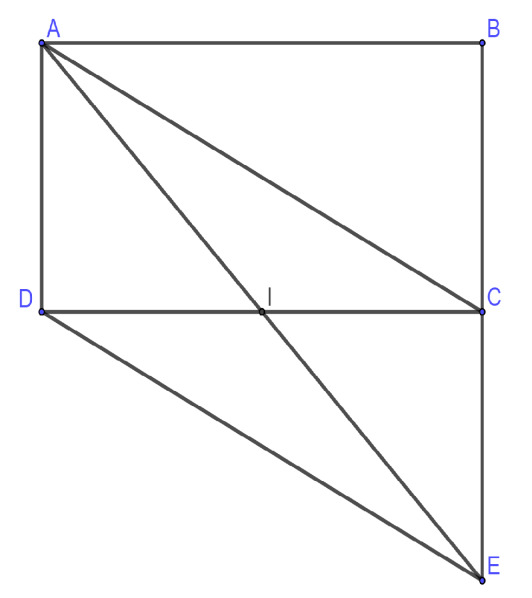
a)Ta thực hiện biến đổi:
$\left| \overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{BC} \right|=\left| \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AD} \right|=\left| \overrightarrow{AC}+\overrightarrow{AD} \right|$.
Dựng điểm $E$ sao cho: $\overrightarrow{CE}=\overrightarrow{AD}$.
Suy ra $ACED$ là hình bình hành.
Theo quy tắc hình bình hành: $\left| \overrightarrow{AC}+\overrightarrow{AD} \right|=\left| \overrightarrow{AE} \right|=AE$.
Tam giác $ABE$ vuông cân tại $B$ nên:$AE=AB\sqrt{2}=2\sqrt{2}$.
b)Ta thực hiện biến đổi:
$\left| \overrightarrow{AC}-\overrightarrow{AB}-\overrightarrow{AI} \right|=\left| \overrightarrow{BC}-\overrightarrow{AI} \right|=\left| \overrightarrow{AD}-\overrightarrow{AI} \right|=\left| \overrightarrow{ID} \right|=ID=\frac{CD}{2}=1$.
4. BÀI TẬP TỰ LUẬN
Bài 1. Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vectơ 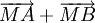 và
và 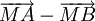 .
.
Bài 2. Cho hình bình hành ABCD và một điểm M tùy ý. Chứng minh rằng 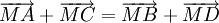 .
.
| Bài 3. Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có: | |
a) 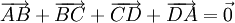 |
b) 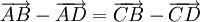 . . |
Bài 4. Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng 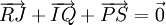 .
.
Bài 5. Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ 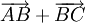 và
và 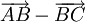 .
.
| bài 6. Cho hình bình hành ABCD có tâm O. Chứng minh rằng: | |
a) 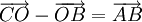 |
b) 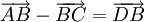 |
c) 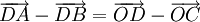 |
d) 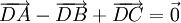 |
Bài 7. Cho 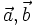 là hai vectơ khác vectơ là hai vectơ khác vectơ  . Khi nào có đẳng thức: . Khi nào có đẳng thức: |
|
a) 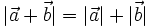 |
b) 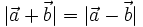 |
Bài 8. Cho 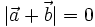 . So sánh độ dài, phương và hướng của hai vectơ
. So sánh độ dài, phương và hướng của hai vectơ  và
và  .
.
Bài 9. Chứng minh rằng 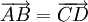 khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
Bài 10. Cho ba lực 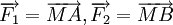 và
và 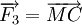 cùng động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của
cùng động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của 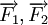 đều là 100N và
đều là 100N và 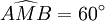 . Tìm cường độ và hướng của lực
. Tìm cường độ và hướng của lực  .
.
5. Ứng dụng thực tiễn
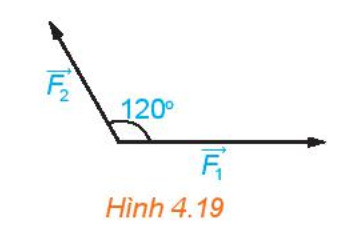
Ví dụ 1. Hình 4.19 biểu diễn hai lực$\overrightarrow{{{F}_{1}}},\,\overrightarrow{{{F}_{2}}}$ cùng tác động lên một vật, cho$\left| \overrightarrow{{{F}_{1}}} \right|=3N,\,\left| \overrightarrow{{{F}_{2}}} \right|=2N$ . Tính độ lớn của hợp lực $\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}$ .
Lời giải
|
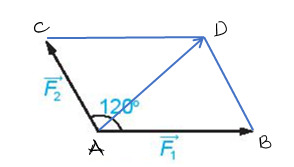
Gọi $\overrightarrow{AB}=\overrightarrow{{{F}_{1}}},\,\overrightarrow{AC}=\overrightarrow{{{F}_{2}}}$ Ta có $\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}=\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}=\overrightarrow{F}$ Xét tam giác$ABD$ ${AD = \sqrt {B{A^2} + B{D^2} – 2BA.BD.{\rm{cos6}}{{\rm{0}}^0}} }$ ${ = \sqrt {9 + 4 – 2.3.2.\frac{1}{2}} = \sqrt 7 .{\rm{\;}}}$ Vậy: $\left| {\vec F} \right| = \sqrt 7 N.$ |
Ví dụ 2.
Hai con tàu xuất phát cùng lúc từ bờ bên này để sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn được giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn ( hình vẽ). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?
Lời giải
Gọi tàu thứ nhất là tàu hướng xuống hạ lưu có vận tốc thực tế là $\overrightarrow{{{v}_{1}}}=\overrightarrow{{{v}_{r}}}+\overrightarrow{{{v}_{n}}}$
tàu thứ hai là tàu hướng lên thượng nguồn có vận tốc thực tế là $\overrightarrow{{{v}_{2}}}=\overrightarrow{{{v}_{r}}}-\overrightarrow{{{v}_{n}}}$
Ta thấy $\overrightarrow{{{v}_{1}}}>\overrightarrow{{{v}_{2}}}$ nên tàu thứ nhất sẽ sang bờ bên kia trước.
6. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho ba vectơ $\vec{a}$, $\vec{b}$ và $\vec{c}$ khác vectơ-không. Trong các khẳng định sau, khẳng định nào sai?
A.$\vec{a}+\vec{b}=\vec{b}+\vec{a}$.
B. $\left( \vec{a}+\vec{b} \right)+\vec{c}=\vec{a}+\left( \vec{b}+\vec{c} \right)$.
C.$\vec{a}+\overrightarrow{0}=\vec{a}$.
D. $\overrightarrow{0}+\vec{a}=\overrightarrow{0}$.
Lời giải
Chọn D
$\overrightarrow{0}+\vec{a}=\vec{a}$.
Câu 2. Cho hình bình hành $ABCD$. Vectơ tổng $\overrightarrow{CB}+\overrightarrow{CD}$ bằng
A. $\overrightarrow{CA}$.
B. $\overrightarrow{BD}$.
C. $\overrightarrow{AC}$.
D. $\overrightarrow{DB}$ .
Lời giải
Chọn A
$\overrightarrow{CB}+\overrightarrow{CD}=\overrightarrow{CA}$.
Câu 3. Cho ba điểm phân biệt$A,B,C$. Trong các khẳng định sau, khẳng định nào sai?
A. $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
B. $\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$.
C. $\overrightarrow{CA}+\overrightarrow{BC}=\overrightarrow{BA}$.
D. $\overrightarrow{CB}+\overrightarrow{AC}=\overrightarrow{BA}$.
Lời giải
Chọn D
$\overrightarrow{CB}+\overrightarrow{AC}=\overrightarrow{AB}$.
Câu 4. Cho bốn điểm phân biệt$A,B,C,D$. Vectơ tổng $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{DA}$ bằng
A. $\overrightarrow{0}$.
B. $\overrightarrow{AC}$.
C. $\overrightarrow{BD}$.
D. $\overrightarrow{BA}$.
Lời giải
Chọn A
$\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{DA}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{AA}=\overrightarrow{0}$.
Câu 5. Cho tam giác $ABC$. Gọi $M,N,P$ lần lượt là trung điểm của $AB,BC,CA$. Vectơ tổng $\overrightarrow{MP}+\overrightarrow{NP}$ bằng
A. $\overrightarrow{BP}$.
B. $\overrightarrow{MN}$.
C. $\overrightarrow{CP}$.
D. $\overrightarrow{PA}$.
Lời giải
Chọn A
$\overrightarrow{MP}+\overrightarrow{NP}=\overrightarrow{BM}+\overrightarrow{MP}=\overrightarrow{BP}$.
Câu 6. Cho hình bình hành $ABCD$ và gọi I là giao điểm của hai đường chéo. Trong các khẳng định sau, khẳng định nào đúng?
A. $\overrightarrow{IA}+\overrightarrow{DC}=\overrightarrow{IB}$.
B.$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{BD}$.
C. $\overrightarrow{IA}+\overrightarrow{BC}=\overrightarrow{IB}$.
D. $\overrightarrow{AB}+\overrightarrow{IA}=\overrightarrow{BI}$.
Lời giải
Chọn A
$\overrightarrow{IA}+\overrightarrow{DC}=\overrightarrow{IA}+\overrightarrow{AB}=\overrightarrow{IB}$.
Câu 7. Cho hình bình hành $ABCD$ và gọi I là giao điểm của hai đường chéo. Trong các khẳng định sau, khẳng định nào sai?
A. $\overrightarrow{IA}+\overrightarrow{DC}=\overrightarrow{IB}$.
B. $\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{BI}=\overrightarrow{DI}$.
C. $\overrightarrow{ID}+\overrightarrow{AB}=\overrightarrow{IC}$.
D. $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CI}=\overrightarrow{IA}$.
Lời giải
Chọn D
$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CI}=\overrightarrow{AC}+\overrightarrow{CI}=\overrightarrow{AI}$.
Câu 8. Cho các điểm phân biệt $M,N,P,Q,R$. Xác định vectơ tổng $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RP}+\overrightarrow{NP}+\overrightarrow{QR}$.
A. $\overrightarrow{MP}$.
B. $\overrightarrow{MN}$.
C. $\overrightarrow{MQ}$.
D. $\overrightarrow{MR}$.
Lời giải
Chọn A
$\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RP}+\overrightarrow{NP}+\overrightarrow{QR}=\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{QR}+\overrightarrow{RP}=\overrightarrow{MP}$.
Câu 9. Cho hình bình hành $ABCD$. Trong các khẳng định sau, khẳng định nào sai?
A. $\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{BC}$.
B. $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.
C. $\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{CB}$.
D. $\overrightarrow{DC}+\overrightarrow{DA}=\overrightarrow{DB}$ .
Lời giải
Chọn C
$\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}=\overrightarrow{BC}$.
Câu 10. Cho tam giác $ABC$ và $M,N,P$ lần lượt là trung điểm của $BC,CA,AB$. Trong các khẳng định sau, khẳng định nào sai?
A. $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\overrightarrow{0}$.
B. $\overrightarrow{AP}+\overrightarrow{BM}+\overrightarrow{CN}=\overrightarrow{0}$.
C. $\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PM}=\overrightarrow{0}$.
D. $\overrightarrow{PB}+\overrightarrow{MC}=\overrightarrow{MP}$ .
Lời giải
Chọn D
$\overrightarrow{PB}+\overrightarrow{MC}=\overrightarrow{PB}+\overrightarrow{BM}=\overrightarrow{PM}$.
Câu 11. Cho lục giác đều $ABCDEF$ có tâm $O$. Trong các khẳng định sau, khẳng định nào sai?.
A. $\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OE}=\overrightarrow{0}$.
B. $\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}=\overrightarrow{EB}$.
C. $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EF}=\overrightarrow{0}$.
D. $\overrightarrow{BC}+\overrightarrow{EF}=\overrightarrow{AD}$ .
Lời giải
Chọn D
$\overrightarrow{BC}+\overrightarrow{EF}=\overrightarrow{0}$.
Câu 12. Cho hình vuông $ABCD$, tâm O. Trong các khẳng định sau, khẳng định nào đúng?
A. $\overrightarrow{BC}+\overrightarrow{AB}=\overrightarrow{CA}$.
B. $\overrightarrow{OC}+\overrightarrow{AO}=\overrightarrow{CA}$.
C. $\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{CA}$.
D. $\overrightarrow{DC}+\overrightarrow{BC}=\overrightarrow{CA}$ .
Lời giải
Chọn A
$\overrightarrow{BA}+\overrightarrow{DA}=\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{CA}$.
Câu 13. Cho lục giác đều $ABCDEF$ có tâm $O$. Trong các khẳng định sau, khẳng định nào sai?.
A. $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}=\overrightarrow{0}$.
B. $\overrightarrow{OA}+\overrightarrow{AB}+\overrightarrow{BO}=\overrightarrow{0}$.
C. $\overrightarrow{OA}+\overrightarrow{FE}=\overrightarrow{0}$.
D. $\overrightarrow{OA}+\overrightarrow{ED}+\overrightarrow{FA}=\overrightarrow{0}$ .
Lời giải
Chọn D
$\overrightarrow{OA}+\overrightarrow{ED}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{FA}$.
Câu 14. Cho tam giác $ABC$ có trọng tâm $G$. Gọi $M$ là trung điểm $BC$, ${{G}_{1}}$ là điểm đối xứng của $G$ qua $M$. Vectơ tổng $\overrightarrow{{{G}_{1}}B}+\overrightarrow{{{G}_{1}}C}$ bằng
A. $\overrightarrow{GA}$.
B. $\overrightarrow{BC}$.
C. $\overrightarrow{{{G}_{1}}A}$.
D. $\overrightarrow{{{G}_{1}}M}$.
Lời giải
Chọn A
$\overrightarrow{{{G}_{1}}B}+\overrightarrow{{{G}_{1}}C}=\overrightarrow{{{G}_{1}}G}=\overrightarrow{GA}$.
Câu 15. Xét tam giác $ABC$ có trọng tâm $G$ và tâm đường tròn ngoại tiếp $O$ thỏa mãn $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$. Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1)$\overrightarrow{OG}=\overrightarrow{0}$;
2) Tam giác $ABC$ là tam giác vuông cân;
3) Tam giác $ABC$ là tam giác đều;
4) Tam giác $ABC$ là tam giác cân.
A. $3$. B.$1$. C. $2$. D. $4$.
Lời giải
Chọn A
$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OG}+\overrightarrow{OG}+\overrightarrow{OG}=\overrightarrow{0}\Rightarrow O\equiv G$. Do đó tam giác $ABC$ là tam giác đều.
Câu 16. Xét tam giác $ABC$ có trọng tâm $H$ và tâm đường tròn ngoại tiếp $O$ thỏa mãn $\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{0}$. Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1) $\overrightarrow{HG}=\overrightarrow{0}$;
2) Tam giác $ABC$ là tam giác vuông cân;
3) $\overrightarrow{OG}=\overrightarrow{0}$;
4) Tam giác $ABC$ là tam giác cân.
A. $3$. B. $1$. C. $2$. D. $4$.
Lời giải
Chọn A
$\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{HG}+\overrightarrow{HG}+\overrightarrow{HG}=\overrightarrow{0}\Rightarrow H\equiv G$. Do đó tam giác $ABC$ là tam giác đều.
Câu 17. Xét tam giác $ABC$ nội tiếp có $O$ là tâm đường tròn ngoại tiếp, $H$ là trực tâm. Gọi $D$ là điểm đối xứng của $A$ qua $O$. Hỏi trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1) $\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{HD}$;
2) $\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{HA}$;
3) $\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{H{{H}_{1}}}$, với ${{H}_{1}}$ là điểm đối xứng của $H$ qua $O$;
4) Nếu $\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{0}$ thì tam giác $ABC$ là tam giác đều.
A. $3$. B. $1$. C. $2$. D. $4$.
Lời giải
Chọn A
$\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{HD}\Rightarrow \overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{H{{H}_{1}}}$.
Nếu $\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{0}$ thì $\overrightarrow{H{{H}_{1}}}=\overrightarrow{0}$, suy ra $H\equiv O$.
Câu 18. Cho $5$ điểm phân biệt $M$, $N$, $P$, $Q$, $R$. Mệnh đề nào sau đây đúng?
A. $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}=\overrightarrow{MP}$.
B. $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}=\overrightarrow{PR}$.
C. $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}=\overrightarrow{MR}$.
D. $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}=\overrightarrow{MN}$.
Lời giải
Chọn D
$\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}=\overrightarrow{MN}$.
Câu 19. Cho hình bình hành $ABCD$, tâm $O$. Vectơ tổng $\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}$ bằng
A. $\overrightarrow{0}$.
B. $\overrightarrow{BD}$.
C. $\overrightarrow{OC}$.
D. $\overrightarrow{OA}$.
Lời giải
Chọn A
$\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{CD}+\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{CC}=\overrightarrow{0}$.
Câu 20. Cho $n$ điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là ${{A}_{1}},{{A}_{2}},…,{{A}_{n}}$. Bạn Bình kí hiệu chúng là ${{B}_{1}},{{B}_{2}},…,{{B}_{n}}$ (${{A}_{1}}\not{\equiv }{{B}_{n}}$). Vectơ tổng $\overrightarrow{{{A}_{1}}{{B}_{1}}}+\overrightarrow{{{A}_{2}}{{B}_{2}}}+…+\overrightarrow{{{A}_{n}}{{B}_{n}}}$ bằng
A. $\overrightarrow{0}$.
B. $\overrightarrow{{{A}_{1}}{{A}_{n}}}$.
C. $\overrightarrow{{{B}_{1}}{{B}_{n}}}$.
D. $\overrightarrow{{{A}_{1}}{{B}_{n}}}$.
Lời giải
Chọn A
Lấy điểm $O$ bất kì. Khi đó
$\overrightarrow{{{A}_{1}}{{B}_{1}}}+\overrightarrow{{{A}_{2}}{{B}_{2}}}+…+\overrightarrow{{{A}_{n}}{{B}_{n}}}=\left( \overrightarrow{{{A}_{1}}O}+\overrightarrow{{{A}_{2}}O}+…+\overrightarrow{{{A}_{n}}O} \right)+\left( \overrightarrow{O{{B}_{1}}}+\overrightarrow{O{{B}_{2}}}+…+\overrightarrow{O{{B}_{n}}} \right)$
Vì $\left\{ {{B}_{1}},{{B}_{2}},…,{{B}_{n}} \right\}=\left\{ {{A}_{1}},{{A}_{2}},…,{{A}_{n}} \right\}$ nên
$\overrightarrow{O{{B}_{1}}}+\overrightarrow{O{{B}_{2}}}+…+\overrightarrow{O{{B}_{n}}}=\overrightarrow{O{{A}_{1}}}+\overrightarrow{O{{A}_{2}}}+…+\overrightarrow{O{{A}_{n}}}$
Do đó $\overrightarrow{{{A}_{1}}{{B}_{1}}}+\overrightarrow{{{A}_{2}}{{B}_{2}}}+…+\overrightarrow{{{A}_{n}}{{B}_{n}}}=\left( \overrightarrow{{{A}_{1}}O}+\overrightarrow{O{{A}_{1}}} \right)+\left( \overrightarrow{{{A}_{2}}O}+\overrightarrow{O{{A}_{2}}} \right)+…+\left( \overrightarrow{{{A}_{n}}O}+\overrightarrow{O{{A}_{n}}} \right)=\overrightarrow{0}$.
Câu 21. Cho $\overrightarrow{a}$ và $\overrightarrow{b}$ là các vectơ khác $\overrightarrow{0}$ với $\overrightarrow{a}$ là vectơ đối của $\ \overrightarrow{b}$. Khẳng định nào sau đây sai?
A. Hai vectơ $\overrightarrow{a},\ \overrightarrow{b}$ cùng phương.
B. Hai vectơ $\overrightarrow{a},\ \overrightarrow{b}$ ngược hướng.
C. Hai vectơ $\overrightarrow{a},\ \overrightarrow{b}$ cùng độ dài.
D. Hai vectơ $\overrightarrow{a},\ \overrightarrow{b}$ chung điểm đầu.
Lời giải
Chọn D
Ta có $\overrightarrow{a}=-\overrightarrow{b}$. Do đó, $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương, cùng độ dài và ngược hướng nhau.
Câu 22. Gọi $O$ là tâm hình bình hành $ABCD$. Đẳng thức nào sau đây sai?
A. $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{CD}.$.
B. $\overrightarrow{OB}-\overrightarrow{OC}=\overrightarrow{OD}-\overrightarrow{OA}.$.
C. $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}.$.
D. $\overrightarrow{BC}-\overrightarrow{BA}=\overrightarrow{DC}-\overrightarrow{DA}.$.
Lời giải
Chọn B
Xét các đáp án:
Đáp án A. Ta có $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}=\overrightarrow{CD}$. Vậy A đúng.
Đáp án B. Ta có
$\left\{ {\begin{array}{*{20}{l}}
{\rm{\;}}&{\overrightarrow {OB} – \overrightarrow {OC} = \overrightarrow {CB} = – \overrightarrow {AD} }\\
{\rm{\;}}&{\overrightarrow {OD} – \overrightarrow {OA} = \overrightarrow {AD} }
\end{array}} \right..$
Vậy B sai.
Đáp án C. Ta có $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB}.$ Vậy C đúng.
Đáp án D. Ta có
$\left\{ {\begin{array}{*{20}{l}}
{\rm{\;}}&{\overrightarrow {BC} – \overrightarrow {BA} = \overrightarrow {AC} }\\
{\rm{\;}}&{\overrightarrow {DC} – \overrightarrow {DA} = \overrightarrow {AC} }
\end{array}} \right.$
Vậy D đúng
Câu 23. Gọi $O$ là tâm hình vuông $ABCD$. Tính $\overrightarrow{OB}-\overrightarrow{OC}$.
A. $\overrightarrow{BC}$.
B. $\overrightarrow{DA}$.
C. $\overrightarrow{OD}-\overrightarrow{OA}$.
D. $\overrightarrow{AB}$.
Lời giải
Chọn B
$\overrightarrow{OB}-\overrightarrow{OC}=\overrightarrow{CB}=\overrightarrow{DA}$.
Câu 24. Cho $O$ là tâm hình bình hành $ABCD$. Hỏi vectơ $\left( \overrightarrow{AO}-\overrightarrow{DO} \right)$ bằng vectơ nào?
A. $\overrightarrow{BA}$.
B. $\overrightarrow{BC}$.
C. $\overrightarrow{DC}$.
D. $\overrightarrow{AC}$.
Lời giải
Chọn B
$\overrightarrow{AO}-\overrightarrow{DO}=\overrightarrow{OD}-\overrightarrow{OA}=\overrightarrow{AD}=\overrightarrow{BC}$.
Câu 25. Chọn khẳng định sai:
A. Nếu $I$là trung điểm đoạn $AB$thì $\overrightarrow{IA}-\overrightarrow{IB}=\overrightarrow{0}$.
B. Nếu $I$là trung điểm đoạn $AB$thì $\overrightarrow{AI}-\overrightarrow{BI}=\overrightarrow{AB}$.
C. Nếu $I$là trung điểm đoạn $AB$thì $\overrightarrow{AI}-\overrightarrow{IB}=\overrightarrow{0}$.
D. Nếu $I$là trung điểm đoạn $AB$thì $\overrightarrow{IA}-\overrightarrow{BI}=\overrightarrow{0}$.
Lời giải
Chọn A
$\overrightarrow{IA}-\overrightarrow{IB}=\overrightarrow{BA}\ne \overrightarrow{0}$.
Câu 26. Cho 4 điểm bất kỳ$A,\text{ }B,\text{ }C,\text{ }D$. Đẳng thức nào sau đây là đúng:
A. $\overrightarrow{OA}=\overrightarrow{CA}+\overrightarrow{CO}$.
B. $\overrightarrow{BC}-\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{0}$.
C. $\overrightarrow{BA}=\overrightarrow{OB}-\overrightarrow{OA}$.
D. $\overrightarrow{OA}=\overrightarrow{OB}-\overrightarrow{BA}$.
Lời giải
Chọn B
$\overrightarrow{BC}-\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{BC}-\overrightarrow{AC}=\overrightarrow{AC}-\overrightarrow{AC}=\overrightarrow{0}$.
Câu 27. Cho các điểm phân biệt$A,\text{ }B,\text{ }C,\text{ }D$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{BC}-\overrightarrow{DA}$.
B. $\overrightarrow{AC}-\overrightarrow{BD}=\overrightarrow{CB}-\overrightarrow{AD}$.
C. $\overrightarrow{AC}-\overrightarrow{DB}=\overrightarrow{CB}-\overrightarrow{DA}$.
D. $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DC}-\overrightarrow{BC}$.
Lời giải
Chọn D
Ta có: $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DB},\text{ }\overrightarrow{DC}-\overrightarrow{BC}=\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB}$.
Vậy: $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DC}-\overrightarrow{BC}$.
Câu 28. Chỉ ra vectơ tổng $\overrightarrow{MN}-\overrightarrow{QP}+\overrightarrow{RN}-\overrightarrow{PN}+\overrightarrow{QR}$ trong các vectơ sau
A. $\overrightarrow{MR}$.
B. $\overrightarrow{MQ}$.
C. $\overrightarrow{MP}$.
D. $\overrightarrow{MN}$.
Lời giải
Chọn D
$\overrightarrow{MN}+\overrightarrow{NP}+\overrightarrow{PQ}+\overrightarrow{QR}+\overrightarrow{RN}=\overrightarrow{MN}$.
Câu 29. Cho hình bình hành $ABCD$và điểm $M$ tùy ý. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{MC}+\overrightarrow{MD}$.
B. $\overrightarrow{MA}+\overrightarrow{MD}=\overrightarrow{MC}+\overrightarrow{MB}$.
C. $\overrightarrow{AM}+\overrightarrow{MB}=\overrightarrow{CM}+\overrightarrow{MD}$.
D. $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$.
Lời giải
Chọn D
Ta có: $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$
${ \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MC} – \overrightarrow {MB} – \overrightarrow {MD} = \vec 0}$
${ \Leftrightarrow \overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} – \overrightarrow {MD} = \vec 0}$
$\Leftrightarrow \overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}.$(đúng).
Câu 30. Cho tam giác $ABC$có $M,\text{ }N,\text{ }D$lần lượt là trung điểm của$AB,\text{ }AC,\text{ }BC$. Khi đó, các vectơ đối của vectơ $\overrightarrow{DN}$ là:
A. $\overrightarrow{AM},\text{ }\overrightarrow{MB},\text{ }\overrightarrow{ND}$.
B. $\overrightarrow{MA},\text{ }\overrightarrow{MB},\text{ }\overrightarrow{ND}$.
C. $\overrightarrow{MB},\text{ }\overrightarrow{AM}$.
D. $\overrightarrow{AM},\text{ }\overrightarrow{BM},\text{ }\overrightarrow{ND}$.
Lời giải
Chọn A.
Nhìn hình ta thấy vectơ đối của vectơ $\overrightarrow{DN}$ là:$\overrightarrow{AM},\text{ }\overrightarrow{MB},\text{ }\overrightarrow{ND}$.
Câu 31. Cho các điểm phân biệt$A,\text{ }B,\text{ }C$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{AB}=\overrightarrow{BC}-\overrightarrow{AC}$.
B. $\overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}$.
C. $\overrightarrow{AB}=\overrightarrow{BC}-\overrightarrow{CA}$.
D. $\overrightarrow{AB}=\overrightarrow{CA}-\overrightarrow{CB}$.
Lời giải
Chọn D
${\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}=\overrightarrow{CD}}$.
Câu 32. Cho hình bình hành $ABCD$ tâm $O$. Khi đó $\overrightarrow{CB}-\overrightarrow{CA}$ bằng
A. ${\overrightarrow{OC}+\overrightarrow{OB}}$.
B. ${\overrightarrow{AB}}$.
C. ${\overrightarrow{OC}+\overrightarrow{DO}}$.
D. ${\overrightarrow{CD}}$.
Lời giải
Chọn B
$\overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}$ (qui tắc 3 điểm).
Câu 33. Cho bốn điểm $A,\text{ }B,\text{ }C,\text{ }D$phân biệt. Khi đó vectơ $\overrightarrow{u}=\overrightarrow{AD}-\overrightarrow{CD}+\overrightarrow{CB}-\overrightarrow{DB}$là:
A. $\overrightarrow{u}=\overrightarrow{0}$.
B. $\overrightarrow{u}=\overrightarrow{AD}$.
C. $\overrightarrow{u}=\overrightarrow{CD}$.
D. $\overrightarrow{u}=\overrightarrow{AC}$.
Lời giải
Chọn D
$\overrightarrow{u}=\overrightarrow{AD}-\overrightarrow{CD}+\overrightarrow{CB}-\overrightarrow{DB}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}$.
Câu 34. Cho bốn điểm $A,\text{ }B,\text{ }C,\text{ }D$ phân biệt. Khi đó vectơ $\overrightarrow{u}=\overrightarrow{AD}-\overrightarrow{CD}+\overrightarrow{CB}-\overrightarrow{AB}$bằng:
A. $\overrightarrow{u}=\overrightarrow{AD}$.
B. $\overrightarrow{u}=\overrightarrow{0}$.
C. $u=\overrightarrow{CD}$.
D. $\overrightarrow{u}=\overrightarrow{AC}$.
Lời giải
Chọn B
$\overrightarrow{u}=\overrightarrow{AD}-\overrightarrow{CD}+\overrightarrow{CB}-\overrightarrow{AB}=\overrightarrow{AD}-\overrightarrow{AB}+\overrightarrow{CB}-\overrightarrow{CD}=\overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}$.
Câu 35. Cho 4 điểm$A,\text{ }B,\text{ }C,\text{ }D$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{AB}-\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{DB}$.
B. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{BC}$.
C. $\overrightarrow{AB}-\overrightarrow{DC}=\overrightarrow{AD}+\overrightarrow{CB}$.
D. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{DA}-\overrightarrow{CB}$.
Lời giải
Chọn C
$\overrightarrow{AB}-\overrightarrow{DC}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$.
Câu 40. Cho Cho hình bình hành $ABCD$ tâm$O$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{AO}+\overrightarrow{BO}-\overrightarrow{CO}+\overrightarrow{DO}=\overrightarrow{0}$.
B. $\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=\overrightarrow{0}$.
C. $\overrightarrow{AO}+\overrightarrow{OB}+\overrightarrow{CO}-\overrightarrow{OD}=\overrightarrow{0}$.
D. $\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{CO}+\overrightarrow{DO}=\overrightarrow{0}$.
Lời giải
Chọn B
Ta có: $\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=\overrightarrow{AO}+\overrightarrow{CO}+\overrightarrow{BO}+\overrightarrow{DO}=\overrightarrow{0}$.
Do $\overrightarrow{AO},\text{ }\overrightarrow{CO}$ đối nhau, $\overrightarrow{BO},\text{ }\overrightarrow{DO}$ đối nhau.
Câu 41. Cho Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
A. $\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{EO}=\overrightarrow{0}$.
B. $\overrightarrow{BC}-\overrightarrow{EF}=\overrightarrow{AD}$.
C. $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{EB}-\overrightarrow{OC}$.
D. $\overrightarrow{AB}+\overrightarrow{CD}-\overrightarrow{EF}=\overrightarrow{0}$.
Lời giải
Chọn D
Ta có: $\overrightarrow{AB}+\overrightarrow{CD}-\overrightarrow{EF}=\overrightarrow{AB}+\overrightarrow{BO}-\overrightarrow{OA}=\overrightarrow{AO}-\overrightarrow{OA}=2\overrightarrow{AO}\ne \overrightarrow{0}$.
Câu 42. Cho hình bình hành $ABCD$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{BA}-\overrightarrow{BC}+\overrightarrow{DC}=\overrightarrow{CB}$.
B. $\overrightarrow{BA}-\overrightarrow{BC}+\overrightarrow{DC}=\overrightarrow{BC}$.
C. $\overrightarrow{BA}-\overrightarrow{BC}+\overrightarrow{DC}=\overrightarrow{AD}$.
D. $\overrightarrow{BA}-\overrightarrow{BC}+\overrightarrow{DC}=\overrightarrow{CA}$.
Lời giải
Chọn A
$\overrightarrow{BA}-\overrightarrow{BC}+\overrightarrow{DC}=\overrightarrow{CA}+\overrightarrow{DC}=\overrightarrow{DC}+\overrightarrow{CA}=\overrightarrow{DA}=\overrightarrow{CB}$.
Câu 43. Cho 4 điểm $A,B,C,D$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$.
B. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{BC}$.
C. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{BD}$.
D. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{DA}+\overrightarrow{BC}$.
Lời giải
Chọn A
$\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\Leftrightarrow \overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\Leftrightarrow \overrightarrow{DB}=\overrightarrow{DB}$.
Câu 44. Cho DABC, vẽ bên ngoài tam giác các hình bình hành ABEF, ACPQ, BCMN. Xét các mệnh đề:
$(I)$ $\overrightarrow{NE}+\overrightarrow{FQ}=\overrightarrow{MP}$
$(II)$ $\overrightarrow{EF}+\overrightarrow{QP}=-\overrightarrow{MN}$
$\left( III \right)$ $\overrightarrow{AP}+\overrightarrow{BF}+\overrightarrow{CN}=\overrightarrow{AQ}+\overrightarrow{EB}+\overrightarrow{MC}$
Mệnh đề đúng là :
A. Chỉ $\left( I \right)$.
B. Chỉ $\left( III \right)$.
C. $\left( I \right)$và $(II)$.
D. Chỉ $(II)$.
Lời giải
Chọn A
$\overrightarrow{NE}+\overrightarrow{FQ}=\overrightarrow{MP}$.
Câu 45. Cho tam giác $ABC$ đều cạnh $a$. Tính $\left| \overrightarrow{AB}+\overrightarrow{AC} \right|.$
A. $\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=a\sqrt{3}$.
B. $\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=\frac{a\sqrt{3}}{2}.$
C. $\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=2a$.
D. $\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=2a\sqrt{3}$.
Lời giải
Chọn A
Gọi $M$ là điểm sao cho $ABMC$là hình bình hành. Ta có $AB=AC$ nên $ABMC$là hình thoi. Gọi O là tâm hình thoi $ABMC$. $\left| \overrightarrow{AB}+\overrightarrow{AC} \right|=\left| \overrightarrow{AM} \right|=AM=2AO=a\sqrt{3}$.
Câu 46. Cho hình vuông $ABCD$ có cạnh bằng $a$. Độ dài $\left| \overrightarrow{AD}+\overrightarrow{AB} \right|$ bằng
A. $2a$
B. $\frac{a\sqrt{2}}{2}$.
C. $\frac{a\sqrt{3}}{2}$.
D. $a\sqrt{2}$.
Lời giải
Chọn D
Theo quy tắc đường chéo hình bình hành, ta có
$\left| \overrightarrow{AD}+\overrightarrow{AB} \right|$$=\left| \overrightarrow{AC} \right|$$=AC$$=AB\sqrt{2}$$=a\sqrt{2}$.
Câu 47. Cho tam giác đều $ABC$ cạnh $a$, mệnh đề nào sau đây đúng?
A. $\left| \overrightarrow{AC} \right|=\overrightarrow{BC}$.
B. $\overrightarrow{AC}=a$.
C. $\overrightarrow{AB}=\overrightarrow{AC}$.
D. $\left| \overrightarrow{AB} \right|=a$.
Lời giải
Chọn D
$\left| \overrightarrow{AB} \right|=AB$ $=a$.
Câu 48. Cho $\overrightarrow{AB}$ khác $\overrightarrow{0}$ và cho điểm $C$.Có bao nhiêu điểm $D$ thỏa $\left| \overrightarrow{AB} \right|=\left| \overrightarrow{CD} \right|$?
A. Vô số.
B. $1$ điểm.
C. $2$ điểm.
D. Không có điểm nào.
Lời giải
Chọn A
Ta có $\left| \overrightarrow{AB} \right|=\left| \overrightarrow{CD} \right|$$\Leftrightarrow AB=CD$.
Suy ra tập hợp các điểm $D$là đường tròn tâm $C$ bán kính $AB$.
Câu 49. Cho tam giác $ABC$ đều có cạnh $AB=5$, $H$ là trung điểm của $BC$. Tính $\left| \overrightarrow{CA}-\overrightarrow{HC} \right|$.
A. $\left| \overrightarrow{CA}-\overrightarrow{HC} \right|=\frac{5\sqrt{3}}{2}$.
B. $\left| \overrightarrow{CA}-\overrightarrow{HC} \right|=5$.
C. $\left| \overrightarrow{CA}-\overrightarrow{HC} \right|=\frac{5\sqrt{7}}{4}$.
D. $\left| \overrightarrow{CA}-\overrightarrow{HC} \right|=\frac{5\sqrt{7}}{2}$.
Lời giải
Chọn D
Gọi $M$ là điểm sao cho $CHMA$ là hình bình hành.
Ta có: $\left| \overrightarrow{CA}-\overrightarrow{HC} \right|=\left| \overrightarrow{CA}+\overrightarrow{CH} \right|=\left| \overrightarrow{CM} \right|=CM=2CE$ ($E$ là tâm cúa hình bình hành$CHMA$).
Ta lại có: $AH=\frac{5\sqrt{3}}{2}$ ($\Delta ABC$ đều, $AH$ là đường cao).
Trong tam giác $HEC$ vuông tại $H$, có:
$EC=\sqrt{C{{H}^{2}}+H{{E}^{2}}}=\sqrt{{{2.5}^{2}}+{{\left( \frac{5\sqrt{3}}{4} \right)}^{2}}}=\frac{5\sqrt{7}}{4}$$\Rightarrow \left| \overrightarrow{CA}-\overrightarrow{HC} \right|=2CE=\frac{5\sqrt{7}}{2}$.
Câu 50. Có hai lực $\overrightarrow{{{F}_{1}}}$, $\overrightarrow{{{F}_{2}}}$ cùng tác động vào một vật đứng tại điểm $O$, biết hai lực $\overrightarrow{{{F}_{1}}}$, $\overrightarrow{{{F}_{2}}}$ đều có cường độ là $50\,\,\left( \text{N} \right)$ và chúng hợp với nhau một góc $60{}^\circ $. Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?
A. $100\,\,\left( \text{N} \right)$.
B. $50\sqrt{3}\,\,\left( \text{N} \right)$.
C. $100\sqrt{3}\,\,\left( \text{N} \right)$.
D. Đáp án khác.
Lời giải
Chọn B
Giả sử $\overrightarrow{{{F}_{1}}}=\overrightarrow{OA}$, $\overrightarrow{{{F}_{2}}}=\overrightarrow{OB}$.
Theo quy tắc hình bình hành, suy ra $\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}=\overrightarrow{OC}$, như hình vẽ.
Ta có $\widehat{AOB}=60{}^\circ $, $OA=OB=50$, nên tam giác $OAB$ đều, suy ra $OC=50\sqrt{3}$.
Vậy $\left| \overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}} \right|=\left| \overrightarrow{OC} \right|=50\sqrt{3}\,\left( \text{N} \right)$.
————————-
Xem thêm:
 và
và 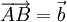 . Vectơ
. Vectơ 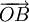 được gọi là tổng của hai vectơ
được gọi là tổng của hai vectơ 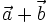 . Vậy
. Vậy 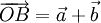 (hình vẽ).
(hình vẽ).

 .
.
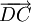 và
và 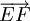 có cùng độ dài nhưng ngược hướng với nhau nên chúng là hai vectơ đối nhau. Do đó, ta có thể viết
có cùng độ dài nhưng ngược hướng với nhau nên chúng là hai vectơ đối nhau. Do đó, ta có thể viết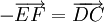 hoặc
hoặc 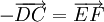
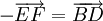 hoặc
hoặc 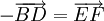
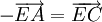 hoặc
hoặc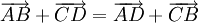 “.
“.


0 Bình luận