Đề 004-TN THPT QG

Đề 004-TN THPT QG

Câu 44. [Mức độ 3] Cho hai hàm số $u\left( x \right)=\frac{x+3}{\sqrt{{{x}^{2}}+3}}$ và $f\left( x \right)$, trong đó đồ thị hàm số $y=f\left( x \right)$ như hình sau.

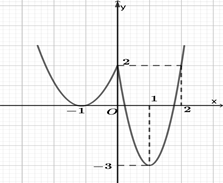
Hỏi có bao nhiêu số nguyên $m$ để phương trình $f\left( u\left( x \right) \right)=m$ có đúng ba nghiệm

phân biệt?

A. $4$.                           

B. $3$.                         

C. $2$.                         

D. $1$.

Hướng dẫn và Lời giải

Chọn đáp án B

Xét hàm số $y=f\left( u\left( x \right) \right)$với $u\left( x \right)=\frac{x+3}{\sqrt{{{x}^{2}}+3}}$.

Ta có:

$\begin{array}{l} y’ = u’\left( x \right).f’\left( {u\left( x \right)} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} u’\left( x \right) = 0\\ f’\left( {u\left( x \right)} \right) = 0 \end{array} \right.{\mkern 1mu} {\mkern 1mu} . \end{array}$

+) $u\left( x \right)=\frac{x+3}{\sqrt{{{x}^{2}}+3}}$$\Rightarrow {u}’\left( x \right)=\frac{\sqrt{{{x}^{2}}+3}-\frac{\left( x+3 \right)x}{\sqrt{{{x}^{2}}+3}}}{{{x}^{2}}+3}=\frac{3-3x}{\left( {{x}^{2}}+3 \right)\sqrt{{{x}^{2}}+3}}$ $\Rightarrow {u}’\left( x \right)=0\Leftrightarrow x=1$.

$\begin{array}{l} + )\,f’\left( {u\left( x \right)} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \frac{{x + 3}}{{\sqrt {{x^2} + 3} }} = – 1\\ \frac{{x + 3}}{{\sqrt {{x^2} + 3} }} = 0\\ \frac{{x + 3}}{{\sqrt {{x^2} + 3} }} = 1 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} VN\\ x = – 3\\ x = – 1 \end{array} \right.\\ \Rightarrow f’\left( {u\left( x \right)} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l} – 1 < \frac{{x + 3}}{{\sqrt {{x^2} + 3} }} < 0\\ 1 < \frac{{x + 3}}{{\sqrt {{x^2} + 3} }} < 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} x < - 3\\ x > – 1 \end{array} \right.\,\,\,. \end{array}$

Ta thấy $\underset{x\to +\infty }{\mathop{\lim }}\,u\left( x \right)=1\Rightarrow \underset{x\to +\infty }{\mathop{\lim }}\,f\left( u\left( x \right) \right)=-3\,\,\text{v }\!\!\grave{\mathrm{a}}\!\!\text{ }\,\,\underset{x\to -\infty }{\mathop{\lim }}\,u\left( x \right)=-1\Rightarrow \underset{x\to -\infty }{\mathop{\lim }}\,f\left( u\left( x \right) \right)=0$.

Bảng biến thiên $y=f\left( u\left( x \right) \right)$

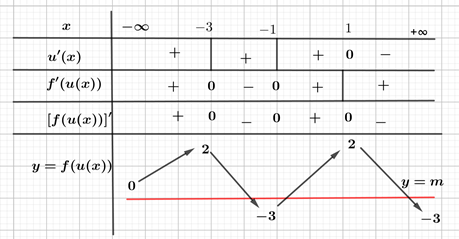
Vậy phương trình $f\left( u\left( x \right) \right)=m$ có 3 nghiệm phân biệt khi và chỉ khi $-3<m\le 0$.

Vì $m\in \mathbb{Z}$ nên $m=\left\{ -2\,;\,-1\,;\,0 \right\}$. Suy ra có 3 giá trị $m$ thỏa mãn yêu cầu bài toán.

Trở lại đề thi