Phần 1. ĐB-NB của hàm số không chứa tham số
Dạng 1. Tìm khoảng ĐB-NB của hàm số cho trước
Dạng 1.1. Biết bảng biến thiên
Ví dụ 1: Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau:
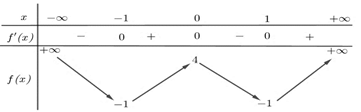
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. $\left( -\infty ;-1 \right)$.
B. $\left( 0;1 \right)$.
C. $\left( -1;1 \right)$.
D. $\left( -1;0 \right)$
Hướng dẫn và lời giải
Dựa vào bảng biến thiên, chọn đáp án C.
Dạng 1.2. Biết bảng dấu y’
Ví dụ: Cho hàm số $y=f\left( x \right)$ có bảng xét dấu đạo hàm như sau

Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng $\left( -\infty ;-2 \right)$
B. Hàm số đồng biến trên khoảng $\left( -2;0 \right)$
C. Hàm số đồng biến trên khoảng $\left( -\infty ;0 \right)$
D. Hàm số nghịch biến trên khoảng $\left( 0;2 \right)$
Hướng dẫn và lời giải
Dựa vào bảng dấu y’, chọn đáp án D.
Dạng 1.3. Biết đồ thị hàm số
Ví dụ: Cho hàm số $y=f\left( x \right)$ có đồ thị (c) như hình vẽ bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
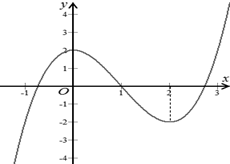
A. $\left( -1;1 \right).$
B. $\left( -1;2 \right).$
C. $\left( 1;2 \right).$
D. $\left( 2;+\infty \right).$
Hướng dẫn và lời giải
Dựa vào đồ thị (c), hàm số nghịch biến trên $\left( 0;2 \right)\supset \left( 1;2 \right).$Vậy chọn đáp án C.
Dạng 1.4. Biết hàm số
Ví dụ: Cho hàm số $y={{x}^{4}}-2{{x}^{2}}$. Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng $\left( -\infty ;\,-2 \right)$
B. Hàm số đồng biến trên khoảng $\left( -1;\,1 \right)$
C. Hàm số nghịch biến trên khoảng $\left( -1;\,1 \right)$
D. Hàm số đồng biến trên khoảng $\left( -\infty ;\,-2 \right)$
Hướng dẫn và lời giải
Txđ: R
$y’=4{{x}^{3}}-4x$
$y’ = 0 \Leftrightarrow 4{x^3} – 4x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = \pm 1} \end{array}} \right.$Bảng bt:
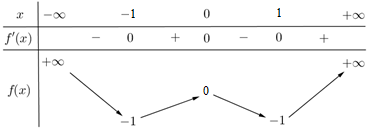
Ta có: Hàm số nghịch biến trên $\left( -\infty ;-1 \right)\supset \left( -\infty ;-2 \right)$. Vậy chọn A.
Dạng 1.5. Cho biết đạo hàm y’.
Ví dụ: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm ${f}’\left( x \right)={{\left( 1-x \right)}^{2}}{{\left( x+1 \right)}^{3}}\left( 3-x \right)$. Hàm số $y=f\left( x \right)$ đồng biến trên khoảng nào dưới đây?
A. $\left( -\infty ;\,1 \right)$.
B. $\left( -\infty ;\,-1 \right)$.
C. $\left( 1;\,3 \right)$.
D. $\left( 3;\,+\infty \right)$.
Hướng dẫn và lời giải
$f'(x)=0\Leftrightarrow x=1;x=-1;x=3$
Lập bảng xét dấu ý, ta có:
| x | -$\infty $ -1 1 3 +$\infty $ |
| f’(x) | – 0 – 0 + 0 – |
Suy ra: hàm số đồng biến trên (1;3). Vậy chọn C.
Dạng 1.6. Tìm hàm số đồng biến nghịch biến trên khoảng cho trước
Ví dụ: Hàm số nào dưới đây đồng biến trên khoảng $\left( -\infty ;+\infty \right)$?
A. $y=\frac{x-1}{x-2}$
B. $y={{x}^{3}}+x$
C. $y=-{{x}^{3}}-3x$
D. $y=\frac{x+1}{x+3}$
Hướng dẫn và lời giải
* Xét A.
Hàm số có TXĐ $x\ne 2$ không liên tục tại x=2, do đó loại đáp án A.
*Xét B.
Hàm số có TXĐ: $\mathbb{R}$
$y’=3{{x}^{2}}+1>0;\forall x\in \mathbb{R}$=> hàm số Đồng biến trên $\mathbb{R}$, Vậy chọn đáp án B.
Phần 2. Hàm số chứa tham số
1. Phương pháp giải
Ba phương pháp tìm điều kiện của tham số sao cho hàm số đồng biến, nghịch biến trên khoảng K.
Phương pháp 1. Phương pháp loại trừ.
Phương pháp 2. Sử dụng Max, Min.
Phương pháp 3. Phương pháp tự luận.
2. Ví dụ minh họa
Cho hàm số $y={{x}^{3}}-3m{{x}^{2}}+1$. Tìm m sao cho hàm số đồng biến trên (2;+$\infty $).
A. $m\le 1$
B. $m\le 0$
C. $0<m\le 1$
D. $m>1$
Hướng dẫn và lời giải
Cách 1. Áp dụng quy tắc 1.
*Trước hết ta nhận xét: m=1 chỉ thuộc đáp án A;C. Ta kiểm tra yêu cầu đề bài với m=1.
Với m=1. Ta có: $y’=3{{x}^{2}}-6x$$y’=0\Leftrightarrow x=0;x=2$
Lập BBT:
| x | -$\infty $ 0 2 +$\infty $ |
| y’ | + 0 – 0 + |
Suy ra hàm số đồng biến trên (2;+$\infty $) thỏa mãn, Vì vậy loại đáp án B; D.
*Nhận xét m=0 thuộc đáp án A nhưng không thuộc đáp án C. Kiểm tra với m=0.
Ta có: $y’=3{{x}^{2}}\ge 0;\forall x\in \mathbb{R}$, suy ra hàm số đồng biến trên $\mathbb{R}$chứa (2;+$\infty $), vậy loại đáp án C và chọn đáp án A.
Kết luận: Chọn đáp án A.
Bình luận: Với quy tắc này các bạn chỉ cần nắm chắc quy tắc lập bảng biến thiên là giải được.
Cách 2. Áp dụng Max, min.
Ta có: $y’=3{{x}^{2}}-6mx$
Hàm số đồng biến trên(2;+$\infty $) khi và chỉ khi $y’\ge 0;\forall x>2$$\Leftrightarrow 3{{x}^{2}}-6mx\ge 0;\forall x>2$$\Leftrightarrow m\le \frac{x}{2};\forall x>2$
$\Leftrightarrow m\le \underset{(2;+\infty )}{\mathop{Min}}\,g(x)$với: $g(x)=\frac{x}{2}$
Khi đó: $g'(x)=\frac{1}{2}>0;\forall x>2$. Suy ra hàm số đồng biến trên (2;+$\infty $), nên $\underset{(2;+\infty )}{\mathop{Min}}\,g(x)=g(2)=1\Leftrightarrow m\le 1.$.
Vậy chọn đáp án A.
Cách 3. Sử dụng tự luận.
Ta có: $y’=3{{x}^{2}}-6mx$
$y’=0\Leftrightarrow x=0;x=2m$.
*Xét trường hợp 1. m=0.
Ta có bảng biến thiên
| x | -$\infty $ 0 +$\infty $ |
| y’ | + 0 + |
Suy ra hàm số đồng biến trên $\mathbb{R}$ nên đồng biến trên (2;+$\infty $). Vậy m=0 thỏa mãn.
* Xét trường hợp 2. m<0.
Ta có bảng biến thiên
| x | -$\infty $ 2m 0 +$\infty $ |
| y’ | + 0 – 0 + |
Suy ra hàm số đồng biến trên $(0;+\infty )$ nên đồng biến trên (2;+$\infty $). Vậy m<0 thỏa mãn.
* Xét trường hợp 3. m>0.
Ta có bảng biến thiên
| x | -$\infty $ 0 2m +$\infty $ |
| y’ | + 0 – 0 + |
Suy ra hàm số đồng biến trên $(2m;+\infty )$ nên đồng biến trên (2;+$\infty $) khi và chỉ khi $2m\le 2\Leftrightarrow m\le 1.$ Vậy $0<m\le 1$ thỏa mãn.
Kết hợp (1);(2);(3) ta có: $m\le 1$.
Kết luận: Chọn đáp án A.
3. Một số dạng thường gặp
Dạng 1. Tìm tham số để hàm số bậc 3 ĐB-NB trên $\mathbb{R}$
Xét hàm số bậc ba $y=f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d.$
– Bước 1. Tập xác định: $D=\mathbb{R}.$
– Bước 2. Tính đạo hàm ${y}’={f}'(x)=3a{{x}^{2}}+2bx+c.$
+ Để $f(x)$ đồng biến trên $\mathbb{R}\Leftrightarrow $
$ \Leftrightarrow y’ = f'(x) \ge 0,{\rm{ }}\forall x \in \mathbb{R} $
$ \Leftrightarrow \left\{ \begin{array}{l} {a_{f'(x)}} = 3a > 0\\ {\Delta _{f'(x)}} = 4{b^2} – 12ac \le 0 \end{array} \right. \Rightarrow m{\rm{ }}?$+ Đề nghịch biến trên $\mathbb{R}$ $ \Leftrightarrow y’ = f'(x) \le 0,{\rm{ }}\forall x \in \mathbb{R}$
$ \Leftrightarrow \left\{ \begin{array}{l} {a_{f'(x)}} = 3a < 0\\ {\Delta _{f'(x)}} = 4{b^2} - 12ac \le 0 \end{array} \right. \Rightarrow m{\rm{ }}?$Lưu ý: Dấu của tam thức bậc hai $f(x)=a{{x}^{2}}+bx+c.$
+Để
$f(x) \ge 0,{\rm{ }}\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l} a > 0\\ \Delta \le 0 \end{array} \right. \cdot $+ Để
$f(x) \le 0,{\rm{ }}\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l} a < 0\\ \Delta \le 0 \end{array} \right. \cdot $Ví dụ:
Có bao nhiêu giá trị nguyên của tham số $m$ sao cho hàm số $f(x)=\frac{1}{3}{{x}^{3}}+m{{x}^{2}}+4x+3$ đồng biến trên $\mathbb{R}$.
A. $5$.
B. $4$.
C. $3$.
D. $2$.
Hướng dẫn và lời giải
Chọn A
Ta có ${f}'(x)={{x}^{2}}+2mx+4$.
Hàm số đã cho đồng biến trên $\mathbb{R}$ khi và chỉ khi ${f}'(x)\ge 0,\,\forall x\in \mathbb{R}$ (Dấu ‘=’ xảy ra tại hữu hạn điểm).
Ta có ${f}'(x)\ge 0,\,\forall x\in \mathbb{R}\Leftrightarrow Delta ‘ \le 0$
$\Leftrightarrow \Delta ‘={{m}^{2}}-4\le 0$
$\Leftrightarrow -2\le m\le 2$.
Vì $m\in \mathbb{Z}$ nên $m\in \left\{ -2;\,-1;\,0;\,1;\,2 \right\}$, vậy có $5$ giá trị nguyên của $m$ thỏa mãn.
Dạng 2. Xét hàm số bậc 1 /bậc 1: $y=f(x)=\frac{ax+b}{cx+d}\cdot $
– Bước 1. Tập xác định: $D=\mathbb{R}\backslash \left\{ -\frac{d}{c} \right\}\cdot $
– Bước 2. Tính đạo hàm ${y}’={f}'(x)=\frac{a.d-b.c}{{{(cx+d)}^{2}}}\cdot $
+ Để $f(x)$ đồng biến trên $D\Leftrightarrow {y}’={f}'(x)>0,\text{ }\forall x\in D\Leftrightarrow a.d-b.c>0\Rightarrow m\text{ }?$
+ Để $f(x)$ nghịch biến trên $D\Leftrightarrow {y}’={f}'(x)<0,\text{ }\forall x\in D\Leftrightarrow a.d-b.c<0\Rightarrow m\text{ }?$
Ví dụ
Cho hàm số $y=\frac{mx-2m-3}{x-m}$ với $m$ là tham số. Gọi $S$ là tập hợp tất cả các giá trị nguyên của $m$ để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của $S$.
A. Vô số B. $3$ C. $5$ D. $4$
Hướng dẫn và giải
Hàm số đồng biến trên TXĐkhi và chỉ khi $ad – cb = m.( – m) – 1.( – 2m – 3) = – {m^2} + 2m + 3 > 0$ $ \Leftrightarrow – 1 < m < 3$.
Do m nguyên nên $m = \left\{ {0;1;2} \right\}$ .
Vậy chọn đáp án B.
Dạng 3. Tìm tham số để hàm số ĐB-NB trên khoảng $\left( {\alpha ;\beta } \right)$
Phương pháp : Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Tìm tham số $m$ để hàm số $y=f\left( x\,;\,m \right)$ đơn điệu trên khoảng $\left( \alpha \,;\,\beta \right)$.
Bước 1: Ghi điều kiện để $y=f\left( x\,;\,m \right)$ đơn điệu trên $\left( \alpha \,;\,\beta \right)$. Chẳng hạn:
$\centerdot $ Đề yêu cầu $y=f\left( x\,;\,m \right)$ đồng biến trên $\left( \alpha \,;\,\beta \right)$$\Rightarrow {y}’={f}’\left( x\,;\,m \right)\ge 0$.
$\centerdot $ Đề yêu cầu $y=f\left( x\,;\,m \right)$ nghịch biến trên $\left( \alpha \,;\,\beta \right)$$\Rightarrow {y}’={f}’\left( x\,;\,m \right)\le 0$.
Bước 2: Độc lập $m$ ra khỏi biến số và đặt vế còn lại là $g\left( x \right)$, có hai trường hợp thường gặp :
$\centerdot \text{ }m\ge g\left( x \right)$, $\text{ }\forall x\in \left( \alpha \,;\,\beta \right)$$\Rightarrow m\ge \underset{\left( \alpha \,;\,\beta \right)}{\mathop{\max }}\,g\left( x \right)$.
$\centerdot \text{ }m\le g\left( x \right)$, $\forall x\in \left( \alpha \,;\,\beta \right)$$\Rightarrow m\le \underset{\left( \alpha \,;\,\beta \right)}{\mathop{\min }}\,g\left( x \right)$.
Bước 3: Khảo sát tính đơn điệu của hàm số $g\left( x \right)$ trên $D$ (hoặc sử dụng Cauchy) để tìm giá trị lớn nhất và giá trị nhỏ nhất. Từ đó suy ra $m$.
Ví dụ
Tập hợp tất cả các giá trị thực của tham số $m$ để hàm số $y={{x}^{3}}-3{{x}^{2}}+\left( 4-m \right)x$ đồng biến trên khoảng $\left( 2;+\infty \right)$ là
A. $\left( -\infty ;1 \right]$
B. $\left( -\infty ;4 \right]$
C. $\left( -\infty ;1 \right)$
D. $\left( -\infty ;4 \right)$
Hướng dẫn và lời giải
Chọn B
Ta có.
${{y}^{‘}}=3{{x}^{2}}-6x+4-m$.$ycbt\Leftrightarrow {{y}^{‘}}\ge 0,\forall x\in \left( 2;+\infty \right)$
$\Leftrightarrow 3{{x}^{2}}-6x+4-m\ge 0,\forall x\in \left( 2;+\infty \right)$$\Leftrightarrow m\le 3{{x}^{2}}-6x+4,\forall x\in \left( 2;+\infty \right)$
$\Leftrightarrow m\le \underset{\left( 2;+\infty \right)}{\mathop{\min }}\,g\left( x \right)$ với $g\left( x \right)=3{{x}^{2}}-6x+4$
Ta có.
${{g}^{‘}}\left( x \right)=6x-6$
${{g}^{‘}}\left( x \right)=0\Leftrightarrow 6x-6=0\Leftrightarrow x=1$
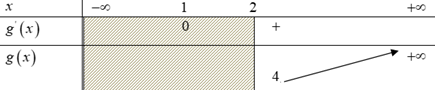
Dựa vào bảng biến thiên, suy ra: $m\le 4$ thỏa yêu cầu bài toán.
Vậy: $m\in \left( -\infty ;4 \right]$ thì hàm số đồng biến trên khoảng $\left( 2;+\infty \right)$.
Phần 3. Tìm khoảng ĐB-NB của Hàm hợp-Hàm ẩn
Dạng 1. Tìm khoảng đơn điệu của hàm số g(x)=f[u(x)] khi biết đồ thị hàm số f’(x)
Cách 1:
Bước 1: Tính đạo hàm của hàm số $g\left( x \right)$, ${g}’\left( x \right)={u}’\left( x \right).{f}’\left[ u\left( x \right) \right]$.
Bước 2: Sử dụng đồ thị của ${f}’\left( x \right)$, lập bảng xét dấu của ${g}’\left( x \right)$.
Bước 3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số.
Cách 2:
Bước 1: Tính đạo hàm của hàm số $g\left( x \right)$, ${g}’\left( x \right)={u}’\left( x \right).{f}’\left[ u\left( x \right) \right]$.
Bước 2: Hàm số $g\left( x \right)$ đồng biến $\Leftrightarrow {g}’\left( x \right)\ge 0$; (Hàm số $g\left( x \right)$ nghịch biến $\Leftrightarrow {g}’\left( x \right)\le 0$) (*)
Bước 3: Giải bất phương trình $\left( * \right)$ (dựa vào đồ thị hàm số $y={f}’\left( x \right)$) từ đó kết luận khoảng đồng biến, nghịch biến của hàm số.
Ví dụ minh họa
Ví dụ 1.
Cho hàm số $y=f(x)$. Hàm số $y=f'(x)$ có đồ thị như hình bên. Hàm số $y=f(2-x)$đồng biến trên khoảng
A. $\left( 2;+\infty \right)$
B. $\left( -2;1 \right)$
C. $\left( -\infty ;-2 \right)$
D. $\left( 1;3 \right)$
Hướng dẫn và lời giải
Chọn B
Cách 1:
Ta thấy $f'(x)<0$ với
nên $f(x)$ nghịch biến trên $\left( 1;4 \right)$ và $\left( -\infty ;-1 \right)$ suy ra $g(x)=f(-x)$ đồng biến trên$(-4;-1)$ và $\left( 1;+\infty \right)$. Khi đó $f(2-x)$ đồng biến biến trên khoảng $(-2;1)$và $\left( 3;+\infty \right)$
Cách 2:
Dựa vào đồ thị của hàm số $y={f}’\left( x \right)$ ta có .
$f’\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l} x < – 1\\ 1 < x < 4 \end{array} \right.$Ta có ${{\left( f\left( 2-x \right) \right)}^{\prime }}={{\left( 2-x \right)}^{\prime }}.{f}’\left( 2-x \right)=-{f}’\left( 2-x \right)$.
Để hàm số $y=f\left( 2-x \right)$ đồng biến thì ${{\left( f\left( 2-x \right) \right)}^{\prime }}>0\Leftrightarrow {f}’\left( 2-x \right)<0$
$ \Leftrightarrow \left[ \begin{array}{l} 2 – x < – 1\\ 1 < 2 – x < 4 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x > 3\\ – 2 < x < 1 \end{array} \right.$Ví dụ 2.
Cho hàm số $f\left( x \right)$, bảng xét dấu của ${f}’\left( x \right)$ như sau:

Hàm số $y=f\left( 5-2x \right)$ đồng biến trên khoảng nào dưới đây?
A. $\left( 3\,;\,4 \right)$.
B. $\left( 1\,;\,3 \right)$.
C. $\left( -\infty \,;\,-3 \right)$.
D. $\left( 4\,;\,5 \right)$.
Hướng dẫn và lời giải
Chọn D
Ta có ${y}’={f}’\left( 5-2x \right)$$=-2{f}’\left( 5-2x \right)$.
${y}’=0$$\Leftrightarrow -2{f}’\left( 5-2x \right)=0$ $ \Leftrightarrow \left[ \begin{array}{l} 5 – 2x = – 3\\ 5 – 2x = – 1\\ 5 – 2x = 1 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} x = 4\\ x = 3\\ x = 2 \end{array} \right.$ ${f}’\left( 5-2x \right)<0$ $ \Leftrightarrow \left[ \begin{array}{l} 5 - 2x < - 3\\ - 1 < 5 - 2x < 1 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} x > 4\\ 2 < x < 3 \end{array} \right.$ $f’\left( {5 – 2x} \right) > 0$ $ \Leftrightarrow \left[ \begin{array}{l} 5 – 2x > 1\\ – 3 < 5 – 2x < – 1 \end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l} x < 2\\ 3 < x < 4 \end{array} \right.$Bảng biến thiên
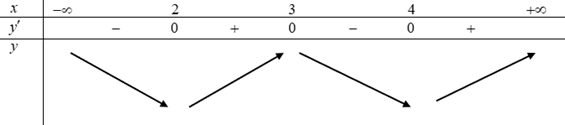
Dựa vào bảng biến thiên hàm số $y=f\left( 5-2x \right)$ đồng biến trên khoảng $\left( 4\,;\,5 \right)$.
————————–
Xem thêm: Tính Đồng biến- Nghịch biến của hàm số.



0 Bình luận