Lý thuyết tìm cực trị của hàm số
–Định lí cực trị
$\centerdot $ Điều kiện cần (định lí 1): Nếu hàm số $y=f(x)$ có đạo hàm trên khoảng $(a;b)$ và đạt cực đại
(hoặc cực tiểu) tại ${{x}_{\circ }}$ thì ${f}'({{x}_{\circ }})=0.$
$\centerdot $ Điều kiện đủ (định lí 2):
Nếu ${f}'(x)$ đổi dấu từ âm sang dương khi $x$ đi qua điểm ${{x}_{\circ }}$ (theo chiều tăng) thì hàm số $y=f(x)$
đạt cực tiểu tại điểm ${{x}_{\circ }}.$
Nếu ${f}'(x)$ đổi dấu từ dương sang âm khi $x$ đi qua điểm ${{x}_{\circ }}$ (theo chiều tăng) thì hàm số $y=f(x)$
đạt cực đại tại điểm ${{x}_{\circ }}.$
$\centerdot $ Định lí 3: Giả sử $y=f(x)$ có đạo hàm cấp $2$ trong khoảng $({{x}_{\circ }}-h;\text{ }{{x}_{\circ }}+h),$ với $h>0.$ Khi đó:
Nếu ${y}'({{x}_{\circ }})=0,\text{ }{y}”({{x}_{\circ }})>0$ thì ${{x}_{\circ }}$ là điểm cực tiểu.
Nếu ${y}'({{x}_{o}})=0,\text{ }{y}”({{x}_{o}})<0$ thì ${{x}_{\circ }}$ là điểm cực đại.
– Các THUẬT NGỮ cần nhớ
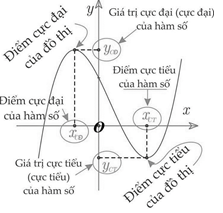
$y=f(x)\Rightarrow \left\{ \begin{align} & {y}'({{x}_{\circ }})=0 \\ & M({{x}_{\circ }};{{y}_{\circ }})\in y=f(x) \\ \end{align} \right.\cdot $$\centerdot $ Điểm cực đại (cực tiểu) của hàm số là ${{x}_{\circ }},$ giá trị cực đại (cực tiểu) của hàm số là $f({{x}_{\circ }})$
(hay ${{y}_{\mathsf{C}}}$ hoặc ${{y}_{\text{CT}}}).$ Điểm cực đại của đồ thị hàm số là $M({{x}_{\circ }};f({{x}_{\circ }})).$
$\centerdot $ Nếu $M({{x}_{\circ }};{{y}_{\circ }})$ là điểm cực trị của đồ thị hàm số:
Phần 1. Tìm cực trị của hàm số không chứa tham số
Dạng 1. Cho biết bảng biến thiên
Ví dụ.
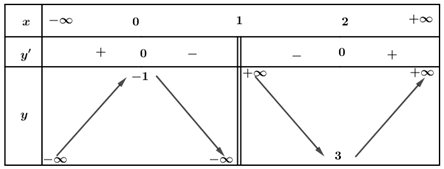
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
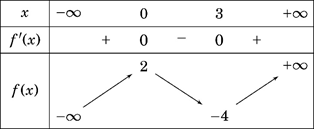
Giá trị cực tiểu của hàm số đã cho bằng
A. $2$. B. $3$. C. $0$. D. $-4$.
Hướng dẫn và lời giải
Chọn D
Từ bảng biến thiên, ta thấy giá trị cực tiểu của hàm số đã cho bằng $-4$.
Dạng 2. Biết đồ thị hàm số
Ví dụ.
Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
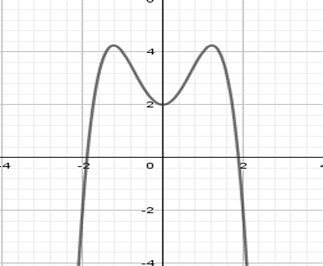
A. $3$ B. $1$ C. $2$ D. $0$
Hướng dẫn và lời giải
Chọn A
Hàm số có ba điểm cực trị.
Dạng 3. Biết bảng dấu y’.
Ví dụ.
Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của ${f}’\left( x \right)$ như sau:
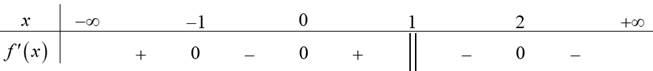
Số điểm cực đại của hàm số đã cho là
A. $4$. B. $1$. C. $2$. D. $3$.
Hướng dẫn và lời giải
Chọn C
Do hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$, ${f}’\left( -1 \right)=0$và ${f}’\left( x \right)$ đổi dấu từ $”+”$ sang $”-”$ khi đi qua các điểm $x=-1$ nên hàm số đã cho đạt cực đại tại điểm $x=-1$.
${f}’\left( 1 \right)$ không xác định nhưng do hàm số liên tục trên $\mathbb{R}$ nên tồn tại $f\left( 1 \right)$ và ${f}’\left( x \right)$ đổi dấu từ $”+”$ sang $”-”$ khi đi qua các điểm $x=1$ nên hàm số đã cho đạt cực đại tại điểm $x=1$.
Vậy số điểm cực đại của hàm số đã cho là 2.
Chọn C.
Dạng 4. Biết đạo hàm y’.
Ví dụ 1.
Cho hàm số $f(x)$ có đạo hàm ${f}'(x)=x(x-1){{(x+2)}^{3}}{{\left( x-2 \right)}^{2}}$, $\forall x\in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là
A. $1$ B. $3$ C. $2$ D. $5$
Hướng dẫn và lời giải
Chọn B
| x | -2 | 0 | 1 | 2 | |||||
| f’(x) | – | 0 | + | 0 | – | 0 | + | 0 | + |
Từ bảng dấu y’ ta có 3 điểm cực trị.
Vậy chọn B.
Dạng 5. Biết đồ thị của f'(x)
Ví dụ 1.
Cho hàm số $y=f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị hàm số $y={f}’\left( x \right)$ là đường cong ở
hình bên.
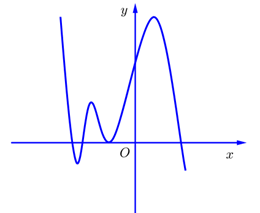
Hỏi hàm số $y=f\left( x \right)$ có bao nhiêu điểm cực trị ?
A. 6.
B. 3.
C. 4.
D. 5.
Lời giải
Chọn B
Đầu tiên ta xác định số nghiệm của f'(x) chính là số giao điểm của đồ thị f'(x) và trục hoành 0x.
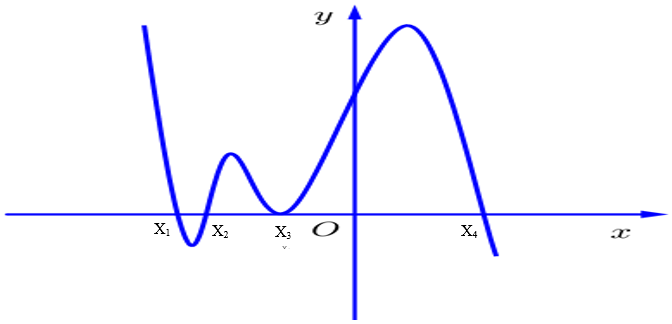
Tiếp sau ta lập bảng dấu của f'(x) dựa vào đồ thị f'(x).
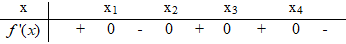
Dựa vào bảng dấu f'(x) ta thấy phương trình ${f}’\left( x \right)=0$ có 4 nghiệm nhưng giá trị ${f}’\left( x \right)$ chỉ đổi dấu 3 lần.
Vậy hàm số $y=f\left( x \right)$ có 3 điểm cực trị.
Dạng 6. Biết hàm số f(x)
Ví dụ.
Giá trị cực đại của hàm số $y={{x}^{3}}-3x+2$ bằng
A. $-1.$
B. $0.$
C. $1.$
D. $4.$
Hướng dẫn và lời giải
Chọn D
Ta có: $y’ = 3{x^2} – 3$
$y’ = 0 \Leftrightarrow x = \pm 1$
Dấu y’:
| x | -1 | 1 | |||
| f’(x) | + | 0 | – | 0 | + |
$ \Rightarrow {x_{c{\rm{d}}}} = – 1;{y_{c{\rm{d}}}} = 4$.
Dạng 7. Tìm hàm số có cực trị cho trước
Ví dụ 1.
Trong các hàm số sau, hàm số nào có 3 điểm cực trị?
A. $y=\frac{x-1}{x+1}$
B. $y={{x}^{3}}-3{{\text{x}}^{2}}+$
C. $y={{x}^{4}}-2{{\text{x}}^{2}}-3$
D. $y=x-\frac{1}{x-1}$
Hướng dẫn và lời giải
Chọn C
+Hàm A. là hàm số bậc1/bậc1 luôn đơn điệu trên tập xác định => loại.
+Hàm B. Là hàm bậc 3 có nhiều nhất 2 cực trị => loại.
+Hàm C. Có $y{\rm{‘}} = 4{x^3} – 4x$; $y{\rm{‘}} = 0 \Leftrightarrow x = 0;x = \pm 1.$ Hàm đa thức bậc 3 có 3 nghiệm phân biệt nên chúng đổi dấu khi qua các nghiệm.
+Hàm D. Là hàm bậc 2/bậc 1 có nhiều nhất 2 cực trị => loại.
Vậy chọn C.
Dạng 8. Tìm cực trị hàm số $y = \left| {f(x)} \right|$
Ví dụ 1.
Biết rằng đồ thị hàm số $y=f(x)$ có dạng như hình vẽ:
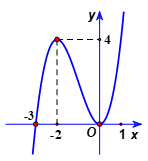
Hỏi đồ thị hàm số $y=\left| f(x) \right|$ có bao nhiêu điểm cực trị?
A. 0. B. 2. C. 1. D. 3.
Lời giải
Chọn D
Xác định đồ thị $y=\left| f(x) \right|$ bằng cách lấy đối xứng qua trục 0x phần đồ thị phía dưới 0x (hình vẽ).
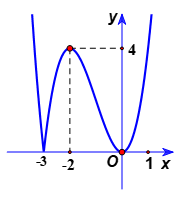
Dựa vào đồ thị $y=\left| f(x) \right|$, ta thấy đồ thị hàm số có 3 điểm cực trị.
Dạng 9. Tìm cực trị của hàm số $y = f\left( {\left| x \right|} \right)$
Ví dụ 1.
Cho hàm số $y=f\left( x \right)$ có đồ thị hình sau.
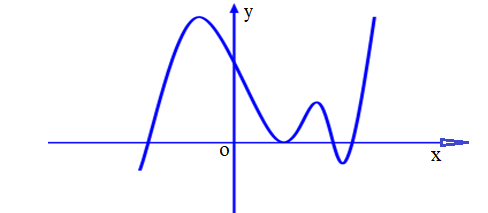
Hàm số $y=f\left( \left| x \right| \right)$ có bao nhiêu điểm cực trị?
A. 3. B. 2. C. 5. D. 7.
Lời giải
Chọn D
Xác định đồ thị $y=f\left( \left| x \right| \right)$ bằng cách giữ nguyên phần đồ thị bên phải trục $Oy$
Lấy đối xứng phần đồ thị nằm trên phải trục $Oy$ qua $Oy$ ta được đồ thị hàm $y=f\left( \left| x \right| \right)$.
Vậy hàm số $y=f\left( \left| x \right| \right)$ có $7$ cực trị.
Hệ quả: Số cực trị của $y=f\left( \left| x \right| \right)$ bằng $2m + 1$ với $m$ là số cực trị có hoành độ dương của $y=f(x)$
Lưu ý: Ngoài hai trường hợp thường gặp trên đây còn có thể gặp các phép biến đổi đồ thị khác. Khi đó tùy theo yêu cầu mà ta biến đổi đồ thị cho phù hợp.
Phần 2. Hàm số chứa tham số.
Dạng 1. Tìm tham số để hàm số đạt cực đại, cực tiểu tại điểm cho trước
Ví dụ.
Xác định giá trị của tham số m để hàm số $y=\frac{{{x}^{2}}+mx+1}{x+m}$đạt cực đại tại $x=2$.
A. m=$-1.$ B. m=$0.$ C. m=$1.$ D. m=$-3$
Hướng dẫn và lời giải
Chọn D
TXĐ: $\mathbb{R}\backslash \{-m\}$
$y’=\frac{{{x}^{2}}+2mx+{{m}^{2}}-1}{{{\left( x+m \right)}^{2}}}$
Hàm số đã cho các đạt cực trị tại $x=2$$\Rightarrow $$y'(2)=0$
$ \Rightarrow {2^2} + 2m.2 + {m^2} – 1 = 0$
$ \Leftrightarrow {m^2} + 4m + 3 = 0$
$ \Leftrightarrow \left[ \begin{array}{l} m = – 1\\ m = – 3 \end{array} \right.$Thử lại:
Với $m=-1$ thì $y’=\frac{{{x}^{2}}-2x}{{{\left( x+1 \right)}^{2}}}$
Lập BBT
Từ BBT ta thấy hàm số đạt cực tiểu tại $x=2$ nên $m=-1$ không phải là giá trị cần tìm.
Với $m=-3$ thì $y’=\frac{{{x}^{2}}-6x+8}{{{\left( x+3 \right)}^{2}}}$
Lập BBT
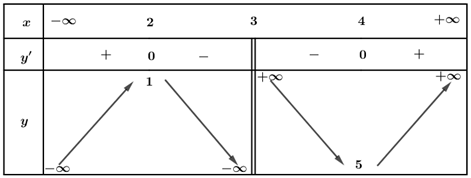
Từ BBT ta thấy hàm số đạt cực đại tại $x=2$ nên $m=-3$ là giá trị cần tìm.
Vậy $m=-3$ là giá trị cần tìm.
Dạng 2. Tìm tham số đề hàm có có n cực trị
Ví dụ.
Tập hợp các giá trị của tham số $m$ để hàm số $y={{x}^{3}}-3m{{x}^{2}}+6mx+m$ có hai điểm cực trị là
A. $\left( 0;2 \right).$
B. $\left( -\infty ;0 \right)\cup \left( 2;+\infty \right).$
C. $\left( 0;8 \right).$
D. $\left( -\infty ;0 \right)\cup \left( 8;+\infty \right).$
Hướng dẫn và lời giải
Chọn B
Ta có ${y}’=3\left( {{x}^{2}}-2mx+2m \right).$Để hàm số có hai điểm cực trị $\Leftrightarrow {y}’=0$ có hai nghiệm phân biệt
$ \Leftrightarrow \Delta ‘ = {m^2} – 2m > 0$
$ \Leftrightarrow \left[ \begin{array}{l} m < 0\\ m > 2 \end{array} \right..$Vậy Chọn B.
Dạng 3. Tìm tham số đề hàm có có cực trị thỏa mãn điều kiện cho trước
Ví dụ 1.
Gọi ${{x}_{1}},\,\text{ }{{x}_{2}}$ là hai điểm cực trị của hàm số$y={{x}^{3}}-3m{{x}^{2}}+3\left( {{m}^{2}}-1 \right)x-{{m}^{3}}+m.$ Tìm các giá trị của tham số $m$ để $x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}}=7.$
A. $m=0.$
B. $m=\pm \frac{1}{2}.$
C. $m=\pm \frac{9}{2}.$
D. $m=\pm 2.$
Hướng dẫn và lời giải
Chọn D
Đạo hàm: ${y}’=3\left[ {{x}^{2}}-2mx+\left( {{m}^{2}}-1 \right) \right].$ Có ${\Delta }’={{m}^{2}}-{{m}^{2}}+1=1>0,\text{ }\forall m\in \mathbb{R}$ nên hàm số luôn có hai điểm cực trị ${{x}_{1}},\,\text{ }{{x}_{2}}.$
Theo định lí Viet, ta có
$\left\{ \begin{array}{l} {x_1} + {x_2} = 2m\\ {x_1}{x_2} = {m^2} – 1 \end{array} \right.$YCBT $\Leftrightarrow {{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-3{{x}_{1}}{{x}_{2}}=7\Leftrightarrow 4{{m}^{2}}-3\left( {{m}^{2}}-1 \right)=7\Leftrightarrow {{m}^{2}}=4\Leftrightarrow m=\pm 2.$
Vậy Chọn D.
Ví dụ 2.
Tìm tất cả các giá trị thực của tham số $m$ để khoảng cách từ điểm $M\left( 0;3 \right)$ đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}+3mx+1$ bằng $\frac{2}{\sqrt{5}}.$
A. $m=\pm 1.$
B.$m=-1$.
C.$m=3,m=-1.$
D. Không tồn tại $m.$
Hướng dẫn và lời giải
Chọn B
Đạo hàm: ${y}’=3{{x}^{2}}+3m;\text{ }{y}’=0\Leftrightarrow {{x}^{2}}=-m.$
Để hàm số có hai điểm cực trị $\Leftrightarrow {y}’=0$ có hai nghiệm phân biệt $\Leftrightarrow m<0$. $\left( * \right)$
Thực hiện phép chia $y$ cho ${y}’$ ta được phần dư $2mx+1.$ Suy ra đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có phương trình $\Delta :y=2mx+1.$
Yêu cầu bài toán $\Leftrightarrow d\left[ M,\Delta \right]=\frac{2}{\sqrt{4{{m}^{2}}+1}}=\frac{2}{\sqrt{5}}\Leftrightarrow {{m}^{2}}=1$
$ \Leftrightarrow d\left[ {M,\Delta } \right] = \frac{2}{{\sqrt {4{m^2} + 1} }} = \frac{2}{{\sqrt 5 }}$ $ \Leftrightarrow {m^2} = 1$ $ \Leftrightarrow \left[ \begin{array}{l} m = 1{\rm{ }}\left( l \right)\\ m = – 1\left( {tm} \right) \end{array} \right.$Ví dụ 3.
Tìm giá trị thực của tham số $m$ để đường thẳng $d:y=\left( 2m-1 \right)x+3+m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+1.$
A.$m=-\frac{1}{2}.$
B.$m=\frac{3}{2}.$
C.$m=\frac{1}{4}.$
D.$m=\frac{3}{4}.$
Hướng dẫn và lời giải
Chọn D
Xét hàm $y={{x}^{3}}-3{{x}^{2}}+1,$ có
$y’ = 3{x^2} – 6x$
$y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0 \to y\left( 0 \right) = 1\\ x = 2 \to y\left( 2 \right) = – {\mkern 1mu} 3 \end{array} \right.$Suy ra $A\left( 0;1 \right),$$B\left( 2;-\,3 \right)$ là hai điểm cực trị của đồ thị hàm số.
Suy ra đường thẳng $AB$ có một VTCP là $\overrightarrow{AB}=\left( 2;-\,4 \right)\xrightarrow{{}}$VTPT ${{\vec{n}}_{AB}}=\left( 2;1 \right).$
Đường thẳng $d:y=\left( 2m-1 \right)x+3+m$ có một VTPT là ${{\vec{n}}_{d}}=\left( 2m-1;-1 \right).$
YCBT $\Leftrightarrow {{\vec{n}}_{AB}}.{{\vec{n}}_{d}}=0\Leftrightarrow 2.\left( 2m-1 \right)-1=0\Leftrightarrow m=\frac{3}{4}.$
Vậy Chọn D.
Ví dụ 4.
Tìm giá trị thực của tham số $m$ để đồ thị hàm số $y=-{{x}^{3}}+3mx+1$có hai điểm cực trị $A,$$B$sao cho tam giác $OAB$ vuông tại $O,$với $O$ là gốc tọa độ.
A. $m=-1.$
B. $m=0.$
C. $m=\frac{1}{2}.$
D. $m=1.$
Hướng dẫn và lời giải
Chọn C
Đạo hàm: ${y}’=-3{{x}^{2}}+3m=-3\left( {{x}^{2}}-m \right).$
Để hàm số có hai điểm cực trị $\Leftrightarrow {{x}^{2}}-m=0$ có hai nghiệm phân biệt $\Leftrightarrow m>0.$
Tọa độ các điểm cực trị của đồ thị hàm số là: $A\left( -\sqrt{m};1-2m\sqrt{m} \right)$ và $B\left( \sqrt{m};1+2m\sqrt{m} \right).$
Yêu cầu bài toán $\Leftrightarrow \overrightarrow{OA}.\overrightarrow{OB}=0\Leftrightarrow 4{{m}^{3}}+m-1=0\Leftrightarrow m=\frac{1}{2}\text{ }\left( tm \right).$
Vậy Chọn C.
Ví dụ 5.
Tìm giá trị thực của tham số $m$ sao cho đồ thị của hàm số $y={{x}^{4}}+2m{{x}^{2}}+1$ có ba điểm cực trị tạo thành tam giác vuông cân.
A. $m=-\frac{1}{\sqrt[3]{9}}.$
B. $m=-1.$
C. $m=\frac{1}{\sqrt[3]{9}}.$
D. $m=1.$
Hướng dẫn và lời giải
Chọn B
Ta có: $y’ = 4{x^3} + 4mx$
$y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} = – m \end{array} \right.$Hàm số có ba điểm cực trị $\Leftrightarrow m<0.$
Toạ độ các điểm cực trị: $A\left( 0;1 \right),\text{ }B\left( \sqrt{-m};-{{m}^{2}}+1 \right)$ và $C\left( -\sqrt{-m};-{{m}^{2}}+1 \right).$
YCBT $ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0$
$ \Leftrightarrow m + {m^4} = 0$
$ \Leftrightarrow \left[ \begin{array}{l} m = 0\left( l \right)\\ m = – 1\left( {tm} \right) \end{array} \right.$Chọn B.
Công thức giải nhanh: Điều kiện để có ba cực trị $ab<0\Leftrightarrow m<0.$
YCBT $\xrightarrow{{}}8a+{{b}^{3}}=0\Leftrightarrow 8.1+{{\left( 2m \right)}^{3}}=0\Leftrightarrow m=-1.$
Ví dụ 6.
Tìm tất cả các giá trị thực của tham số $m$ để đồ thị hàm số $y={{x}^{4}}-2m{{x}^{2}}+1$ có ba điểm cực trị $A\left( 0;1 \right),$$B,$$C$ thỏa mãn $BC=4.$
A.$m=\sqrt{2}.$
B.$m=\pm \sqrt{2}.$
C.$m=4.$
D.$m=\pm 4.$
Hướng dẫn và lời giải
Chọn C
Ta có:
$y’ = 4x\left( {{x^2} – m} \right)$
$y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} = m \end{array} \right.$Hàm số có ba điểm cực trị $\Leftrightarrow m>0.$
Tọa độ các điểm cực trị: $A\left( 0;1 \right),\text{ }B\left( \sqrt{m};1-{{m}^{2}} \right)$ và $\text{ }C\left( -\sqrt{m};1-{{m}^{2}} \right).$
YCBT: $BC=4\Leftrightarrow 2\sqrt{m}=4\Leftrightarrow \sqrt{m}=2\Leftrightarrow m=4$ (thỏa mãn).
Vậy Chọn C.
Công thức giải nhanh: Điều kiện để có ba cực trị $ab<0\Leftrightarrow m>0.$
YCBT: $BC={{m}_{0}}\to am_{0}^{2}+2b=0\Leftrightarrow {{1.4}^{2}}+2.\left( -2m \right)=0\Leftrightarrow m=4.$
Phần 3. Cực trị hàm ẩn-Hàm hợp
Ví dụ 1.
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ
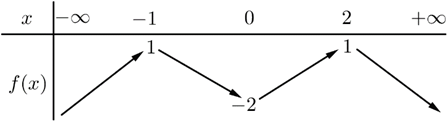
Hàm số $g\left( x \right)=f\left( 2x \right)$ đạt cực đại tại
A. $x=-2.$ B. $x=-1.$ C. $x=\frac{1}{2}.$ D. $x=1.$
Hướng dẫn và lời giải
Chọn D
Ta có ${g}’\left( x \right)=2{f}’\left( 2x \right);$
$g’\left( x \right) = 2f’\left( {2x} \right);$
$g’\left( x \right) = 0 \Leftrightarrow f’\left( {2x} \right) = 0$
$\left[ \begin{array}{l} 2x = – 1\\ 2x = 0\\ 2x = 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = – 0,5\\ x = 0\\ x = 1 \end{array} \right.$Bảng biến thiên
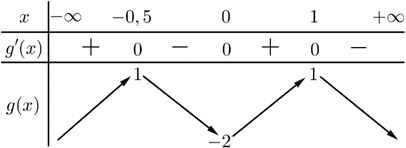
Dựa vào BTT, ta thấy hàm số $g\left( x \right)$ đạt cực đại tại $x=-\frac{1}{2}$ và tại $x=1.$
Chọn D.
Ví dụ 2.
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
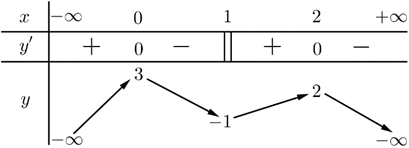
Hàm số $g\left( x \right)=f\left( 3-x \right)$ có bao nhiêu điểm cực trị?
A. $2.$ B. $3.$ C. $5.$ D. $6.$
Hướng dẫn và lời giải
Chọn B
Ta có ${g}’\left( x \right)=-{f}’\left( 3-x \right).$
$g’\left( x \right) = 0 \Leftrightarrow f’\left( {3 – x} \right) = 0$
$\mathop {\mathop \Rightarrow \limits^{{\rm{theo BBT}}} }\limits^{} \left[ \begin{array}{l} 3 – x = 0\\ 3 – x = 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = 3\\ x = 1 \end{array} \right.$$\bullet $${g}’\left( x \right)$ không xác định $\Leftrightarrow 3-x=1\Leftrightarrow x=2.$
Bảng biến thiên
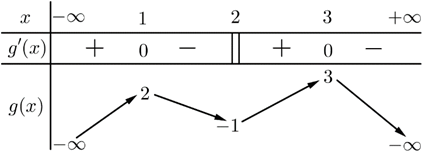
Vậy hàm số $g\left( x \right)=f\left( 3-x \right)$ có $3$ điểm cực trị.
=> Chọn B.
——————
Xem thêm: Cực trị hàm số.

0 Bình luận