Đề 002- TN THPT QG

Đề 002- TN THPT QG

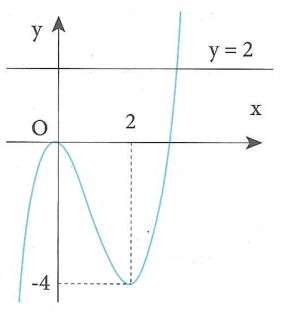
Câu 46. Cho hàm số $y=f(x)$ có đồ thị như hình bên dưới. Hàm số $g(x)=f(f(x))$ đồng biến trên khoảng nào?

A. $\left( 0;2 \right)$        

B. $\left( -\infty ;0 \right)$

C. $\left( 0;4 \right)$        

D. $\left( -1;1 \right)$

Hướng dẫn và lời giải

Đáp án B

Dựa vào đồ thị ta thấy $f(x)$ đạt cực trị tại 0 và 2

Suy ra

$f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.$

Ta có

$g’\left( x \right) = f’\left( x \right)f’\left( {f(x)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.\\ f’\left( {f(x)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l} f(x) = 0 \Leftrightarrow x = 0;x = a > 2\\ f(x) = 2 \Leftrightarrow x = b > a \end{array} \right. \end{array} \right.$

Vậy phương trình ${g}’\left( x \right)=0$ có 4 nghiệm bội lẻ là $x=0,x=2,x=a$ và $x=b$. Lập bảng biến thiên của hàm số $g\left( x \right)=f\left( f\left( x \right) \right)$ ta có được đáp án đúng.

Trở lại đề thi