Góc giữa đường thẳng và mặt phẳng- p1

Góc giữa đường thẳng và mặt phẳng

I. Lý thuyết

1. Định nghĩa:

• Nếu đường thẳng a vuông góc với (P) thì ta nói góc giữa đường thẳng a và mặt phẳng (P) bằng 90⁰ .
• Nếu đường thẳng a không vuông góc với (P) thì góc giữa đường thẳng a và mặt phẳng (P) là góc giữa a và hình chiếu a’ của a trên (P).

Kí hiệu: $\widehat {\left( {a,(P)} \right)}$.

Chú ý: $\widehat {\left( {a,(P)} \right)} = \widehat {\left( {a,a’} \right)}$ với a’ là hình chiếu của a trên (P).

Hệ quả:

• ${0^0} \le \widehat {\left( {a,(P)} \right)} \le {90^0}.$
• $\widehat {\left( {a,(P)} \right)} = {0^0}$ khi và chỉ khi a//(P) hoặc $a \subset (P)$.
• $\widehat {\left( {a,(P)} \right)} = {90^0} \Leftrightarrow a \bot (P).$

2. Phương pháp xác định góc giữa đường thẳng a và mặt phẳng (P).

Phương pháp 1. (Phương pháp hình học)

+ Tìm $I=d\cap (P)$

+ Tìm A thuộc d kẻ AH vuông góc với (P)

+ $(d,(P))=\widehat{AIH}$

Phương pháp 2. (Phương pháp vec tơ)

+ Gọi $\overrightarrow u = (a;b)$ là véc tơ chỉ phương của đướng thẳng a.

+ Gọi $\overrightarrow n = (A;B)$ là véc tơ pháp tuyến của (P).

=>$\sin \alpha = \sin \widehat {\left( {a,(P)} \right)} = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {aA + bB} \right|}}{{\sqrt {{a^2} + {b^2}} \sqrt {{A^2} + {B^2}} }}$

II.Ví dụ minh họa

A. Sử dụng phương pháp hình học

Ví dụ 1.

Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, $SA=a\sqrt{6}$. Tính sin của góc giữa:

a). SC và (SAB)

b). AC và (SBC)

Giải

a).Ta có: $BC\bot AB\text{ (gt)}$ và $SA\bot BC$ (vì $SA\bot (ABCD)$)$\Rightarrow $$BC\bot (SAB)$ do đó: SB là hình chiếu vuông góc của SC trên mp(SAB) $\Rightarrow (SC,(SAB))=\widehat{BSC}$. Ta có: $\begin{align}

  & \Rightarrow \sin (SC,(SAB))=\sin \widehat{BSC}= \\

 & =\frac{BC}{SC}=\frac{a}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{\sqrt{2}}{4} \\ \end{align}$

b) Trong mp(SAB) kẻ $AH\bot SB\text{ (H}\in \text{SB)}$. Theo a) $BC\bot (SAB)\Rightarrow AH\bot BC$ nên $AH\bot (SBC)$ hay CH là hình chiếu vuông góc của AC trên mp(SBC) $\Rightarrow (AC,(SBC))=\widehat{ACH}$.

+ Xét tam giác vuông SAB có: $\frac{1}{A{{H}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{S{{A}^{2}}}=\frac{7}{6{{a}^{2}}}\Rightarrow AH=a.\sqrt{\frac{6}{7}}$

+ Vậy $\sin (AC,(SBC))=\sin \widehat{ACH}=\frac{AH}{AC}=\frac{\sqrt{21}}{7}$

Ví dụ 2.

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $(SAB)\bot (ABCD)$, H là trung điểm của AB, SH=HC, SA=AB. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

Giải

+ Ta có: $AH=\frac{1}{2}AB=\frac{a}{2},$ $SA=AB=a$, $SH=HC=\sqrt{B{{H}^{2}}+B{{C}^{2}}}=\frac{a\sqrt{5}}{2}$.

Vì $S{{A}^{2}}+A{{H}^{2}}=\frac{5{{a}^{2}}}{4}=A{{H}^{2}}$ nên tam giác SAH vuông tại A hay $SA\bot AB$ mà $(SAB)\bot (ABCD)$ . Do đó, $SA\bot (ABCD)$ và AC là hình chiếu vuông góc của SC lên mp(ABCD).

+ Ta có: $(SC,(ABCD))=\widehat{SCA}$, $\tan \widehat{SCA}=\frac{SA}{AC}=\frac{\sqrt{2}}{2}$. Vậy góc giữa đường thẳng SC và mặt phẳng (ABCD) là góc có tang bằng $\frac{\sqrt{2}}{2}$.

Ví dụ 3.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).

A. 30°               B. 45°               C. 60°               D. 75°

Giải

Gọi H là trung điểm của BC suy ra: $AH = BH = CH = \frac{1}{2}BC = \frac{a}{2}$.

Ta có: $SH \bot (ABC) \Rightarrow SH = \sqrt {S{B^2} – B{H^2}} = \frac{{a\sqrt 3 }}{2}$

$\widehat {(SA,(ABC))} = \widehat {SAH} = \alpha $

$ \Rightarrow \tan \alpha = \frac{{SH}}{{AH}} = \sqrt 3 \Rightarrow \alpha = {60^0}$.

Vậy chọn: A.

Ví dụ 4.

Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD) . Biết SA = a(√6)/3. Tính góc giữa SC và (ABCD) .

A. 30°                B. 45°                C. 60°               D.90°

Giải

Ta có: $SA \bot (ABCD) \Rightarrow SA \bot AC$

$ \Rightarrow \widehat {(SC,(ABCD))} = \widehat {SCA} = \alpha $

Vì ABCD là hình vuông cạnh a, nên $AC = a\sqrt 2 ,SA = \frac{{a\sqrt 6 }}{3}$

$ \Rightarrow \tan \alpha = \frac{{SA}}{{AC}} = \frac{{\sqrt 3 }}{3} \Rightarrow \alpha = {30^0}$

Vậy chọn A.

Ví dụ 5.

Cho hình chóp S. ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)

A. 60°               B.90°               C. 45°                D. 30°

Giải

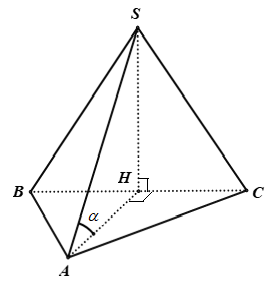
Do H là hình chiếu của S lên mặt phẳng ( ABC) nên SH ⊥ (ABC)

Vậy AH là hình chiếu của SH lên mp(ABC)

⇒ (SA, (ABC)) = (SA, AH) =$\widehat {SAH}$

Ta có: SH ⊥ (ABC) ⇒ SH ⊥ AH

Mà: ΔABC = ΔSBC ⇒ SH = AH

Vậy tam giác SAH vuông cân tại H ⇒ $\widehat {SAH}$ = 45°

=>Chọn C

B. Sử dụng phương pháp véc tơ

(Xem phần 2)

III. Bài tập trắc nghiệm

Câu 1. Cho hình thoi ABCD có tâm O, AC = 2a ; BD = 2AC . Lấy điểm S không thuộc (ABCD) sao cho SO ⊥ (ABCD) . Biết tan(SBO) = 1/2. Tính số đo của góc giữa SC và ( ABCD)

A. 30°               B.45°               C. 60°                D. 90°

Câu 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điể BC . Biết SB = a. Tính số đo của góc giữa SA và (ABC)

A. 30°               B.45°               C. 60°                D. 75°

Câu 3. Cho hình chóp S. ABC có SA ⊥ (ABC) và tam giác ABC không vuông. Gọi H, K lần lượt là trực tâm tam giác ABC và tam giác SBC. Số đo góc tạo bởi SC và (BHK) là:

A. 45°                  B. 120°                  C. 90°                  D. 65°

Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với mp( ABCD). Gọi α là góc giữa BD và mp(SAD) . Chọn khẳng định đúng trong các khẳng định sau?

A. $\alpha = {60^0}$                   B. $\alpha = {30^0}$                  

C. $\cos \alpha = \frac{{\sqrt 6 }}{4}$                  D. $\sin \alpha = \frac{{\sqrt 6 }}{4}$

Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = ${a\sqrt 6 }$. Gọi α là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau ?

A. $\alpha = {60^0}$                   B. $\alpha = {30^0}$                  

C. $ \alpha ={45^0} $                  D. $\cos \alpha = \frac{{\sqrt 3 }}{3}$

Câu 6. Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi α là góc giữa AC’ và mp(A’BCD’). Chọn khẳng định đúng trong các khẳng định sau?

A. $\alpha = {30^0}$                   B. $\alpha = {45^0}$                  

C. $\tan \alpha = \frac{2}{{\sqrt 3 }}$                  D. $\tan \alpha = \sqrt 2 $

Câu 7. Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, SA = 2a và SA vuông góc với mặt phẳng đáy (ABCD), góc giữa cạnh SC và mặt phẳng (ABCD) là?

A. $\tan \beta = \sqrt 2 $                   B. $\tan \beta = \sqrt 5 $                 

C. $\tan \beta = 3 $                  D. $\tan \alpha = 2 $

Câu 8. Cho hình chóp SABCD đáy ABCD là hình chữ nhật. AB=a, AD=2a, cạnh bên SA vuông góc với đáy. Góc giữa SC và đáy ABCD bằng 60⁰ . Tính độ dài SA?

A. $SA = a\sqrt 5 $                 B. $SA = a\sqrt 3 $             

C. $SA = a\sqrt 15 $                  D. $SA = a\sqrt 13 $

Câu 9. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A, B biết AB=BC=a, AD=2a, SA vuông góc với mặt phẳng đáy (ABCD). Tính độ dài SA để góc giữa SC và mặt phẳng (ABCD) bằng 45⁰ .

A. $SA = a\sqrt 5 $                 B. $SA = a\sqrt 3 $             

C. $SA = a\sqrt 6 $                  D. $SA = a\sqrt 2 $

Câu 10. Cho hình chóp SABC có SA = a, SA vuông góc với đáy, ABC là tam giác vuông cân tại B, góc $\widehat {ACB} = {30^0}$, AC=2a. Tính $\tan \alpha $ góc giữa SC và mặt phẳng (SAB).

A. $\tan \alpha = \frac{{\sqrt 5 }}{2}$                 B. $\tan \alpha = \frac{{\sqrt 6 }}{2}$            

C. $\tan \alpha = \frac{{1 }}{2}$                  D. $\tan \alpha = \frac{{\sqrt 3 }}{2}$

———————————-

Xem thêm:

• Góc giữa hai đường thẳng trong không gian.
• Góc giữa đường thẳng và mặt phẳng-p2.
• Góc giữa hai mặt phẳng trong không gian-p1.
• Góc giữa hai mặt phẳng trong không gian-p2.