KHOẢNG CÁCH GIỮA HAI ĐƯỜNG THẲNG CHÉO NHAU
CÁC PHƯƠNG PHÁP GIẢI TOÁN
I. Định nghĩa
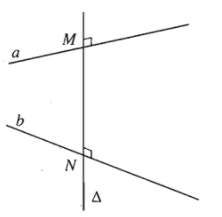
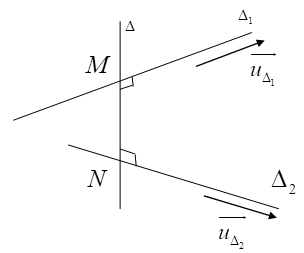
a) Đường thẳng $\Delta $ cắt hai đường thẳng chéo nhau $a,\text{ }b$ và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của $a$ và $b$.
b) Nếu đường vuông góc chung $\Delta $ cắt hai đường thẳng chéo nhau $a,\text{ }b$ lần lượt tại $M,N$ thì độ dài đoạn thẳng $MN$ gọi là khoảng cách giữa hai đường thẳng chéo nhau $a$ và $b$.
II. Các phương pháp giải toán
1. Phương pháp độ dài đoạn vuông góc chung
a. Quy tắc đường vuông góc chung giữa hai đường thẳng chéo nhau
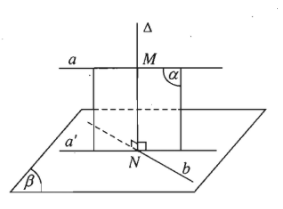
Cho hai đường thẳng chéo nhau $a$ và $b$. Gọi $\left( \beta \right)$ là mặt phẳng chứa $b$ và song song với $a$, ${a}’$ là hình chiếu vuông góc của $a$ lên $\left( \beta \right)$. Vì $a\text{//}\left( \beta \right)\Rightarrow {a}’\text{//}a$. Do đó ${a}’$ và $b$ cắt nhau tại một điểm. Gọi điểm này là $N$. Gọi $\left( \alpha \right)$ là mặt phẳng chứa $a$ và ${a}’$, $\Delta $ là đường thẳng đi qua $N$ và vuông góc với $\left( \beta \right)$. Khi đó $\left( \beta \right)\bot \left( \alpha \right)$ . Như vậy $\Delta $ nằm trong $\left( \alpha \right)$ và cắt $a$ tại $M$, cắt $b$ tại $N$, hơn nữa $\Delta $ vuông góc với cả $a$ và $b$. Vậy $MN$ là đoạn vuông góc chung của $a$ và $b$.
Nhận xét:
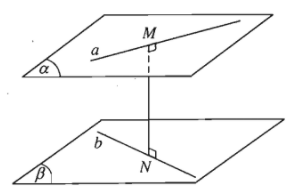
a) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó và mặt phẳng song song với nó chứa mặt phẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
b. Ví dụ điển hình
Bài toán 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh $a$; SA vuông góc đáy, $SA=a$. Gọi O là giao của AC và BD. Tính khoảng cách giữa BD và SC.
Lời giải
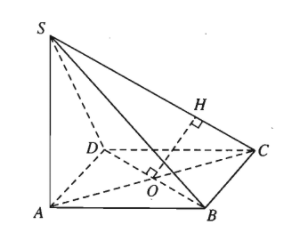
Gọi $O$ là tâm của hình vuông $ABCD$. Trong mặt phẳng $\left( SAC \right)$ vẽ $OH\bot SC$ (hình trên).
Ta có $BD\bot AC$ và nên $BD\bot \left( SAC \right)$, suy ra $BD\bot OH$.
Mặt khác $OH\bot SC$. Vậy $OH$ là đoạn vuông góc chung của $SC$ và $BD$. Độ dài đoạn $OH$ là khoảng cách giữa hai đường thẳng chéo nhau $SC$ và $BD$.
Hai tam giác vuông $SAC$ và $OHC$ đồng dạng vì có chung góc nhọn $C$.
Do đó $\frac{SA}{SC}=\frac{OH}{OC}\left( =\sin C \right)$.
Vậy $OH=\frac{SA.OC}{SC}$.
Ta có $SA=a,OC=\frac{a\sqrt{2}}{2}$ , $SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=\sqrt{{{a}^{2}}+2{{a}^{2}}}=a\sqrt{3}$ nên $OH=\frac{a.\frac{a\sqrt{2}}{2}}{a\sqrt{3}}=\frac{a\sqrt{6}}{6}$
Vậy khoảng cách giữa hai đường thẳng chéo nhau $SC$ và $BD$ là $OH=\frac{a\sqrt{6}}{6}$.
Bài toán 2 : Cho hình lăng trụ đứng $ABC.ABC$có đáy $ABC$là tam giác vuông, $AB=BC=a$, cạnh bên $AA=a\sqrt{2}.$ Gọi $M$ là trung điểm của $BC$. Tính khoảng cách giữa hai đường thẳng $AM$ và $B’C$.
Hướng dẫn và lời giải

Gọi $N$ là trung điểm của $BC$thì $CB//MN$nên $CB//\left( AMN \right).$
Vậy $d\left( BC,AM \right)=d\left( BC,\left( AMN \right) \right)=\left( B,\left( AMN \right) \right)$ $=d\left( B,\left( AMN \right) \right).$
Kẻ $BI\bot AM$ và kẻ $BE\bot NI$thì $BE\bot \left( AMN \right)$ nên $BE$ là khoảng cách cần tìm. $\frac{1}{B{{E}^{2}}}=\frac{1}{B{{I}^{2}}}+\frac{1}{B{{N}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{B{{M}^{2}}}+\frac{1}{B{{N}^{2}}}\Rightarrow BE=\frac{a\sqrt{7}}{7}$
2. Phương pháp tọa độ
a. Công thức khoảng cách
b. Ví dụ điển hình
Bài toán 1.
Trong không gian với hệ tọa độ Oxyz cho đường thẳng ${{\Delta }_{1}}$ có phương trình:$\left\{ \begin{matrix} x=1+2t \\ y=-1+3t \\ z=5+t \\ \end{matrix} \right.$ và đường thẳng ${{\Delta }_{2}}$ có phương trình: $\left\{ \begin{matrix} x=1+3t’ \\ y=-2+2t’ \\ z=-1+2t’ \\ \end{matrix} \right.$. Tính khoảng cách giữa hai đường thẳng trên.Lời giải
$\overrightarrow {{u_{\Delta 1}}} = (2;3;1);A(1; – 1;5) \in {\Delta _1}.$
$\overrightarrow {{u_{\Delta 2}}} = (3;2;2);B(1; – 2;1) \in {\Delta _2}.$
$\left[ {\overrightarrow {{u_{\Delta 1}}} ,\overrightarrow {{u_{\Delta 2}}} } \right] = (4; – 1; – 5);\overrightarrow {AB} = (0; – 1; – 4).$
$d\left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {\left[ {\overrightarrow {{u_{\Delta 1}}} ,\overrightarrow {{u_{\Delta 2}}} } \right].\overrightarrow {AB} } \right|}}{{\left| {\left[ {\overrightarrow {{u_{\Delta 1}}} ,\overrightarrow {{u_{\Delta 2}}} } \right]} \right|}} = \frac{{\sqrt 2 }}{2}$Ví dụ 2.
Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có tam giác $ABC$ vuông tại $A$. AB=a, AC=a\sqrt{3}, $A{A}’=2a$. Hình chiếu vuông góc của điểm $A$ trên mặt phẳng $\left( {A}'{B}'{C}’ \right)$ trung với trung điểm $H$ của đoạn ${B}'{C}’$ (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng $A{A}’$ và $B{C}’$ bằng
A. $\frac{a\sqrt{5}}{3}.$
B. $\frac{a\sqrt{15}}{5}.$
C. $\frac{a\sqrt{5}}{5}.$
D. $\frac{a\sqrt{5}}{5}.$
Hướng dẫn và Lời giải
Cách 1. Phương pháp hình không gian
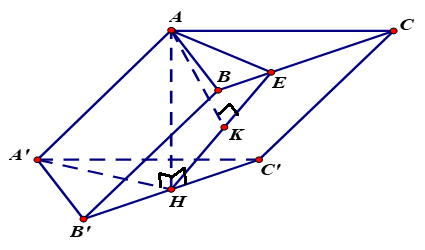
$AA’//\left( {BCC’A’} \right) \Rightarrow d\left( {AA’,{\mkern 1mu} BC’} \right) = d\left( {AA’,{\mkern 1mu} \left( {BCC’B’} \right)} \right) = d\left( {A,{\mkern 1mu} \left( {BCC’B’} \right)} \right).$
Dựng $AE$ vuông góc với $BC$ tại $E$.
Lúc đó $\left( AHE \right)\bot \left( BC{C}'{B}’ \right)$.
Dựng $AK$ vuông góc với $EH$ tại $K$. Lúc đó $AK\bot \left( BC{C}'{B}’ \right)$.
Do đó $d\left( {AA’,{\mkern 1mu} BC’} \right) = AK$
Tính $AK$:
Vì ba cạnh $AB,\,AC,\,AH$ đôi một vuông góc và $AK\bot \left( BCH \right)$
nên ta có $\frac{1}{A{{K}^{2}}}=\frac{1}{A{{B}^{2}}}+\frac{1}{A{{C}^{2}}}+\frac{1}{A{{H}^{2}}}$$=\frac{1}{{{a}^{2}}}+\frac{1}{{{\left( a\sqrt{3} \right)}^{2}}}+\frac{1}{A{{H}^{2}}}=\frac{4}{3{{a}^{2}}}+\frac{1}{A{{H}^{2}}}$.
Ta lại có $A{{H}^{2}}={A}'{{A}^{2}}-{A}'{{H}^{2}}$.
Vì tam giác ${A}'{B}'{C}’$ vuông tại ${A}’$ và có $H$ là trung điểm của ${B}'{C}’$ nên ${A}’H=\frac{{B}'{C}’}{2}$.
Ta có ${B}'{C}’=BC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2a$
do đó ${A}’H=a$
suy ra $A{{H}^{2}}={A}'{{A}^{2}}-{A}'{{H}^{2}}=3{{a}^{2}}$.
$\frac{1}{A{{K}^{2}}}=\frac{4}{3{{a}^{2}}}+\frac{1}{A{{H}^{2}}}=\frac{4}{3{{a}^{2}}}+\frac{1}{3{{a}^{2}}}=\frac{5}{3{{a}^{2}}}$ $\Rightarrow AK=\frac{a\sqrt{15}}{5}$.
Vậy $d\left( A{A}’,\,B{C}’ \right)=\frac{a\sqrt{15}}{5}$.
Cách 2. Phương pháp tọa độ trong không gian
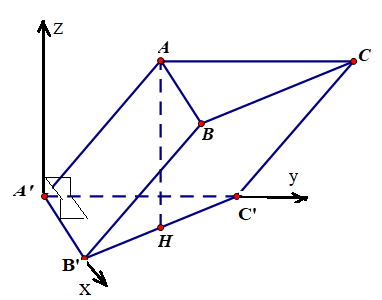
$AA’//\left( {BCC’A’} \right) \Rightarrow d\left( {AA’,BC’} \right) = d\left( {AA’,\left( {BCC’B’} \right)} \right) = d\left( {A,\left( {BCC’B’} \right)} \right)$
Ta có: $A{{H}^{2}}={A}'{{A}^{2}}-{A}'{{H}^{2}}$.
Vì tam giác ${A}'{B}'{C}’$ vuông tại ${A}’$ và có $H$ là trung điểm của ${B}'{C}’$
nên ${A}’H=\frac{{B}'{C}’}{2}$.
Ta có ${B}'{C}’=BC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2a$
do đó ${A}’H=a$ suy ra $A{{H}^{2}}={A}'{{A}^{2}}-{A}'{{H}^{2}}=3{{a}^{2}}\Rightarrow AH=a\sqrt{3}$.
Dựng hệ trục tọa độ 0xyz sao cho: 0 trùng A’; A’z song song với HA, A’B’=0x;A’C’=0y.
Ta suy ra được:
$A'(0;0;0);B'(a;0;0);C'(0;a\sqrt 3 ;0);$
$H(\frac{a}{2};\frac{{a\sqrt 3 }}{2};0) = > A(\frac{a}{2};\frac{{a\sqrt 3 }}{2};a\sqrt 3 )$
Lại có: $\overrightarrow {A’B’} = \overrightarrow {AB} \Rightarrow B(\frac{a}{2};\frac{{a\sqrt 3 }}{2};a\sqrt 3 )$.
${\overrightarrow {B’B} = ( – \frac{a}{2};\frac{{a\sqrt 3 }}{2};a\sqrt 3 ) \Rightarrow \vec u = ( – \sqrt 3 ;1;2)}$
${\overrightarrow {B’C’} = ( – a;a\sqrt 3 ;0) \Rightarrow \vec v = ( – 1;\sqrt 3 ;0)}$
${ \Rightarrow \left[ {\vec u,\vec v} \right] = (2\sqrt 3 ;{\rm{ – 2}}; – 2)}$
${ \Rightarrow {{\vec n}_{(B’BCC’)}} = (\sqrt 3 ; – 1; – 1)}$
Phương trình (B’BCC’) là:
${\sqrt 3 (x – a) – 1(y – 0) – 1(z – 0) = 0}$
${ \Leftrightarrow \sqrt 3 x – y – x – a\sqrt 3 = 0}$
Vậy: $d(A’;(B’BCC’) = \frac{{\left| {a\sqrt 3 } \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{( – 1)}^2} + {{( – 1)}^2}} }} = \frac{{a\sqrt 3 }}{{\sqrt 5 }} = \frac{{a\sqrt {15} }}{5}.$
——————————




0 Bình luận