THIẾT DIỆN CỦA $\left( \alpha \right)$ VỚI HÌNH CHÓP KHI BIẾT $\left( \alpha \right)$ SONG SONG VỚI MỘT MẶT PHẲNG $\left( \beta \right)$CHO TRƯỚC..

THIẾT DIỆN CỦA $\left( \alpha  \right)$ VỚI HÌNH CHÓP KHI BIẾT $\left( \alpha  \right)$ SONG SONG VỚI MỘT MẶT PHẲNG $\left( \beta  \right)$CHO TRƯỚC..

A. Phương pháp

Để xác định thiết diện trong trường hợp này ta sử dụng các tính chất sau:

• Khi $\left( \alpha  \right)\parallel \left( \beta  \right)$ thì $\left( \alpha  \right)$ sẽ song song với tất cả các đường thẳng trong $\left( \beta  \right)$ và ta chuyển về dạng thiết diện song song với đường thẳng.

Sử dụng:

\[\left\{ \begin{array}{l}
\left( \alpha \right)\parallel \left( \beta \right)\\
\left( \beta \right)\parallel \left( \gamma \right)\\
\left( \beta \right) \cap \left( \gamma \right) = d\\
M \in \left( \alpha \right) \cap \left( \gamma \right)
\end{array} \right. \Rightarrow \left( \alpha \right) \cap \left( \gamma \right) = d’\parallel d,M \in d’\]

• Tìm đường thẳng $d$ nằm trong $\left( \beta  \right)$ và xét các mặt phẳng có trong hình chóp mà chứa $d$, khi đó $\left( \alpha  \right)\parallel d$ nên sẽ cắt các mặt phẳng chứa $d$ ( nếu có) theo các giao tuyến song song với $d$.

B. VÍ DỤ MINH HỌA

Ví dụ 1.

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành và $M,N$ lần lượt là trung điểm của $AB,CD$. Xác định thiết diện của hình chóp cắt bởi $\left( \alpha  \right)$ đi qua $MN$ và song song với mặt phẳng $\left( SAD \right)$.Thiết diện là hình gì?

A. Tam giác                              B. Hình thang                        

C. Hình bình hành             D. Tứ giác

Giải

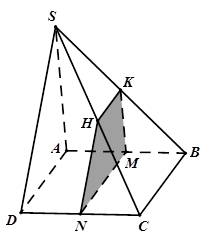
Ta có

$\left\{ \begin{array}{l}
M \in \left( {SAB} \right) \cap \left( \alpha \right)\\
\left( {SAB} \right) \cap \left( {SAD} \right) = SA
\end{array} \right.$

$ \Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = MK\parallel SA,K \in SB$

Tương tự

$\left\{ \begin{array}{l}
N \in \left( {SCD} \right) \cap \left( \alpha \right)\\
\left( \alpha \right)\parallel \left( {SAD} \right)\\
\left( {SCD} \right) \cap \left( {SAD} \right) = SD
\end{array} \right.$

$ \Rightarrow \left( {SCD} \right) \cap \left( \alpha \right) = NH\parallel SD,H \in SC$

Dễ thấy $HK=\left( \alpha  \right)\cap \left( SBC \right)$. Thiết diện là tứ giác $MNHK$. Ba mặt phẳng $\left( ABCD \right),\left( SBC \right)$ và $\left( \alpha  \right)$ đôi một cắt nhau theo các giao tuyến là $MN,HK,BC$, mà $MN\parallel BC\Rightarrow MN\parallel HK$.

Vậy thiết diện là một hình thang .

Ví dụ 2.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M, N, P lần lượt là trung điểm các cạnh AB, CD, SA.

a) Chứng minh $\left( SBN \right)\parallel \left( DPM \right)$.

b) Q là một điểm thuộc đoạn SP (Q khác S,P). Xác định thiết diện của hình chóp cắt bởi $\left( \alpha  \right)$ đi qua Q và song song với $\left( SBN \right)$.

c) Xác định thiết diện của hình chóp cắt bởi $\left( \beta  \right)$ đi qua MN song song với $\left( SAD \right)$.

Giải

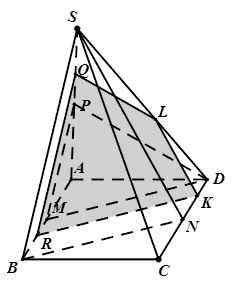
a) Ta có

$\left\{ \begin{array}{l}
BN\parallel DM\\
DM \subset \left( {DPM} \right)
\end{array} \right. \Rightarrow BN\parallel \left( {DPM} \right){\rm{ }}\left( 1 \right)$

Tương tự

$\left\{ \begin{array}{l}
BS\parallel MP\\
MP \subset \left( {DPM} \right)
\end{array} \right. \Rightarrow BS\parallel \left( {DPM} \right){\rm{ }}\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $\left( SBN \right)\parallel \left( DPM \right)$.

b) Ta có

$\left\{ \begin{array}{l}
SB \subset \left( {SBN} \right)\\
\left( \alpha \right)\parallel \left( {SBN} \right)
\end{array} \right. \Rightarrow SB\parallel \left( \alpha \right)$

Vậy $\begin{array}{l}
\left\{ \begin{array}{l}
Q \in \left( {SAB} \right) \cap \left( \alpha \right)\\
SB \subset \left( {SAB} \right)\\
SB\parallel \left( \alpha \right)
\end{array} \right.\\
\Rightarrow \left( {SAB} \right) \cap \left( \alpha \right) = QR\parallel SB,R \in AB
\end{array}$

Tương tự

$\left( \alpha  \right)\cap \left( ABCD \right)=RK\parallel BN,K\in CD$

$\left( \alpha  \right)\cap \left( SCD \right)=KL\parallel SB,L\in SD$.

Vậy thiết diện là tứ giác $QRKL$.

c) ta có:

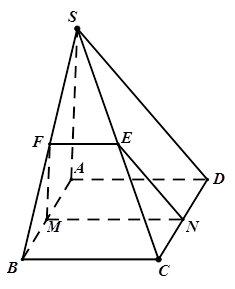
$\begin{array}{l}
\left\{ \begin{array}{l}
M \in \left( \beta \right) \cap \left( {SAB} \right)\\
SA\parallel \left( \beta \right)\\
SA \subset \left( {SAB} \right)
\end{array} \right.\\
\Rightarrow \left( \beta \right) \cap \left( {SAB} \right) = MF\parallel SA,F \in SB
\end{array}$

Tương tự $\left( \beta  \right)\cap \left( SCD \right)=NE//SD,E\in SC$.

Thiết diện là hình thang $MNEF$.

————————