Ứng dụng thực tế tích phân vào tính thể tích của vật thể

Lý thuyết: Ứng dụng tích phân vào tính thể tích của vật thể

1.Công thức tổng quát

Một vật thể \(\Omega\) giới hạn bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại x =a , x = b ( a < b). Một mặt phẳng tùy ý vuông góc với Ox tại hoành độ x ( a < x < b) và cắt \(\Omega\) theo thiết diện S(x) (hàm phụ thuộc vào hoành độ x) và là hàm liên tục theo biến x trên [a, b]. Khi đó thể tích của \(\Omega\) là (thừa nhận):

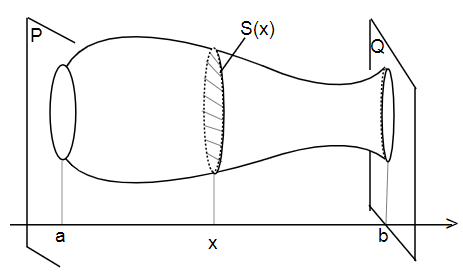
     \(V=\int\limits^b_aS\left(x\right)\text{d}x\)

2. Công thức thể tích hình lăng trụ

Tính thể tích hình lăng trụ biết diện tích đáy là B và chiều cao h (xem hình vẽ)

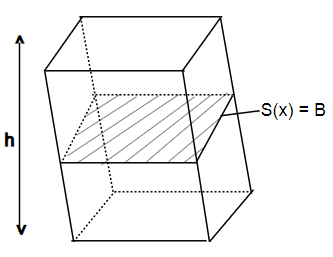
Áp dụng công thức ở trên:

    \(V=\int\limits^h_0S\left(x\right)\text{d}x=\int\limits^h_0B\text{d}x=B.x|^h_0=B.h\)

3. Thể tích khối chóp và khối chóp cụt

a) Khối chóp

Tính thể tích hình chóp có diện tích đáy B và chiều cao h (xem hình vẽ dưới)

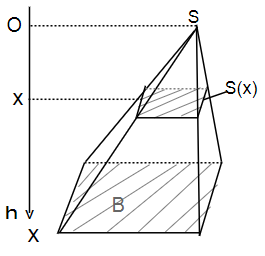
Ta có thiết diện và đáy tỉ lệ với x/h => Diện tích thiết diện và diện tích đáy tỉ lệ với (x/h)² (do diện tích bằng tích hai độ dài).

Hay là: \(\frac{S\left(x\right)}{B}=\frac{x^2}{h^2}\) => \(S\left(x\right)=\frac{B.x^2}{h^2}\)

Theo công thức tính thể tích:

   \(V=\int\limits^h_0S\left(x\right)\text{d}x=\int\limits^h_0\frac{B.x^2}{h^2}\text{d}x=\frac{B}{h^2}.\frac{x^3}{3}|^h_0=\frac{B.h}{3}\)

b) Khối chóp cụt

Thể tích khối chóp cụt có diện tích đáy dưới là \(B_1\) , diện tích đáy trên là \(B_2\)  và chiều cao là h:

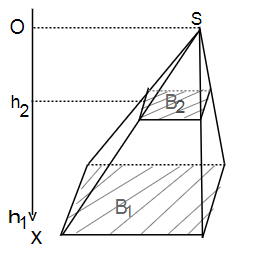
\(V=\int\limits^{h_1}_{h_2}\frac{B_1x^2}{h_1^2}\text{d}x=\frac{B_1}{h_1^2}.\frac{x^3}{3}|^{h_1}_{h_2}=\frac{B_1}{3h_1^2}\left(h_1^3-h_2^3\right)\)

   \(=\frac{B_1\left(h_1-h_2\right)}{3}\frac{\left(h_1^2+h_1h_2+h_2^2\right)}{h_1^2}\)

Thay \(h_1-h_2=h\) và \(\left(\frac{h_2}{h_1}\right)^2=\frac{B_2}{B_1}\) ta có:

   \(V=\frac{h}{3}\left(B_1+\sqrt{B_1B_2}+B_2\right)\)

Chú ý: Có thể tính thể tích khối chóp cụt bằng hiệu hai thể tích khối chóp.

4. Tính thể tích khối tròn xoay.

• Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left(x\right)\), trục hoành và hai đường thẳng \(x=a;x=b\) quanh trục Ox là 

     \(V_x=\pi\int\limits^b_af^2\left(x\right)dx\)  (vì thiết diện là hình tròn bán kính \(f\left(x\right)\))

• Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left(x\right)\), \(y=g\left(x\right)\) (trong đó \(f\left(x\right)\) và \(g\left(x\right)\) cùng dấu) và hai đường thẳng \(x=a;x=b\) quanh trục Ox là 

     \(V_x=\pi\int\limits^b_a\left|f^2\left(x\right)-g^2\left(x\right)\right|dx\) (vì thiết diện là hình miệng giếng giới hạn bởi hai đường tròn bán kính lần lượt là \(f\left(x\right)\) và \(g\left(x\right)\))

 • Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(x=g\left(y\right)\)), trục hoành và hai đường thẳng \(y=a;y=b\) quanh trục Oy là 

     \(V_y=\pi\int\limits^b_ag^2\left(y\right)dy\)

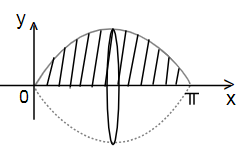
Ví dụ 1: Cho hình phẳng giới hạn bởi đường cong \(y=\sin x\), trục hoành và hai đường thẳng \(x=0;x=\pi\). Hãy tính thể tích của khối tròn xoay khi quay hình này quanh trục Ox.

Giải: Thể tích của khối tròn xoay là:

    \(V=\pi\int\limits^{\pi}_0\sin^2x\text{d}x\)

        \(=\pi\int\limits^{\pi}_0\frac{1}{2}\left(1-\cos2x\right)\text{d}x=\frac{\pi}{2}\left(x-\frac{1}{2}\sin2x\right)|^{\pi}_0=\frac{\pi^2}{2}\)

Ví dụ 2: Tính thể tích khối tròn xoay tạo thành do hình phẳng \(H=\{y=x\ln x; y=0; x=1; x=e\}\) quay quanh Ox.
ĐS: \(V=\dfrac{\pi}{27}(5e^3-3)\) (đvtt)

———————–

Download tài liệu: PDF-tại đây Word: tại đây.

——————

Xem thêm:

• Phương pháp tính tích phân
• Phương pháp tính tích phân từng phần
• Phương pháp tính tích phân bằng đổi biến loại 1
• Phương pháp tính tích phân bằng đổi biến loại 2
• Phương pháp tính tích phân bằng nhân liên hợp
• Phương pháp tính tích phân hàm dưới dấu trị tuyệt đối
• Phương pháp tính tích phân các hàm có dạng đặc biệt
• Một số dạng thường gặp trong tính tich phân
• Ứng dụng tich phân vào tính thể tích
• Ứng dụng tích phân vào tính diện tích hình phẳng

———————–