Đề 003-TN THPT QG

Câu 40. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $A$. Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với $(ABC)$. Lấy M thuộc cạnh SC sao cho $CM=2MS$. Biết khoảng cách giữa hai đường $AC$ và $BM$ bằng $\frac{4\sqrt{21}}{7}\,$. Thể tích khối chóp $S.ABC$ bằng

A. $\frac{16\sqrt{3}}{3}$.

B. $16\sqrt{3}$.           

C.$\frac{32\sqrt{3}}{3}$.       

D. $\frac{32}{3}$.

Hướng dẫn và Lời giải

Chọn A

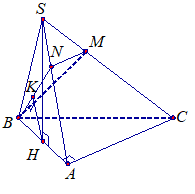
 Gọi H là trung điểm của AB suy ra $SH\bot (ABC)$.

Trong (SAC) từ M dựng MN//AC,  gọi K là hình chiếu của H trên BN.

Ta có $AC\bot (SAB)$mà MN//AC$\Rightarrow MN\bot (SAB)$

$\left\{ {\begin{array}{*{20}{c}} {HK \bot BN}\\ {HK \bot MN} \end{array}} \right. \Rightarrow HK \bot (BMN)$

 Vì (BMN)//AC suy ra  $d\left( AC,BM \right)=$$d\left( A,\left( BMN \right) \right)=2d\left( H,\left( BMN \right) \right)=2HK=d\left( A,BN \right)$

$\Rightarrow d\left( A,BN \right)=\frac{4\sqrt{21}}{7}\,$

Đặt $AB=x\,\,\,\left( x>0 \right)$. Ta có $AN=\frac{2}{3}x\Rightarrow {{S}_{ABN}}=\frac{1}{2}AB.AN.\sin {{60}^{0}}=\frac{\sqrt{3}{{x}^{2}}}{6}$.

Có $B{{N}^{2}}=A{{B}^{2}}+A{{N}^{2}}-2AB.AN.\cos {{60}^{0}}=\frac{7}{9}{{x}^{2}}$$\Rightarrow BN=\frac{x\sqrt{7}}{3}$.

Mặt khác ${{S}_{ABN}}=\frac{1}{2}BN.d\left( A,BN \right)\Rightarrow \frac{\sqrt{3}{{x}^{2}}}{6}=\frac{1}{2}.\frac{x\sqrt{7}}{3}.\frac{4\sqrt{21}}{7}\Rightarrow x=4$.

Khi đó $SH=4.\frac{\sqrt{3}}{2}=2\sqrt{3};\,\,\,\,{{S}_{ABC}}=\frac{1}{2}AB.AC=\frac{1}{2}A{{B}^{2}}=8$.

Trở lại đề thi