Đề 003-TN THPT QG

Đề 003-TN THPT QG

Câu 43. Cho hàm số $y=\frac{ax-1}{bx-c}$$\left( a,b,c\in \mathbb{R} \right)$ có bảng biến thiên như sau:

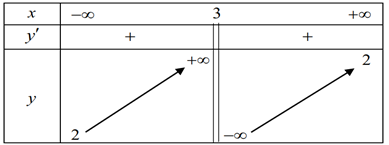
                Trong các số $a,b,c$ có bao nhiêu số dương?

A.$1$.                             

B.$0$.                          

C.$2$.                          

D.$3$.

Hướng dẫn và Lời giải

Chọn D

Dựa vào bảng biến thiên, suy ra:

• Tiệm cận đứng của đồ thị hàm số $x=3$$\Rightarrow \frac{c}{b}=3\Leftrightarrow c=3b$.
• Tiệm cận ngang của đồ thị hàm số $y=2$$\Rightarrow \frac{a}{b}=2\Leftrightarrow a=2b$.
• ${f}’\left( x \right)>0$$\Rightarrow -ac+b>0$.

Từ ba điều kiện trên suy ra:$ac-b<0\Leftrightarrow 6{{b}^{2}}-b<0\Leftrightarrow 0<b<\frac{1}{6}$.

Vậy cả ba số $a,b,c$ đều dương.

CÁCH 2.

• Tiệm cận đứng $x=\frac{c}{b}=3$$\Rightarrow $$b,c$ cùng dấu
• Tiệm cận ngang $y=\frac{a}{b}=2$$\Rightarrow a,b$ cùng dấu
• Nhánh trái của đồ thị cắt trục \[Oy\] tại điểm có tung độ dương nên $\frac{1}{c}>0$$\Rightarrow $$c>0$.

Mà $a,b,c$ cùng dấu nên cả ba số $a,b,c$ cùng dương.

Trở lại đề thi