Câu 46.1. Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ
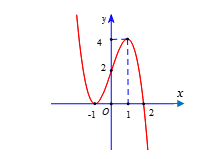
Số nghiệm của phương trình $f\left( \left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right| \right)=2$ là
A. $3$.
B. $6$.
C. $9$.
D. $10$.
Hướng dẫn và Lời giải
Chọn C
Xét hàm số $g\left( x \right)={{x}^{3}}-3{{\text{x}}^{2}}+2$
Ta có
$g’\left( x \right) = 3{{\rm{x}}^2} – 6{\rm{x}} = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = 2 \end{array} \right.$Bảng biến thiên
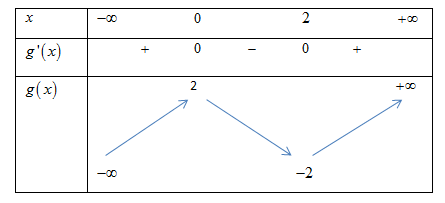
Ta có bảng biến thiên của hàm số $t=\left| g\left( x \right) \right|=\left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right|$
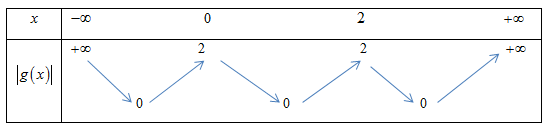
Khi đó phương trình $f\left( \left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right| \right)=2$ trở thành phương trình $f\left( t \right)=2$.
Dựa vào đồ thị ta có
$f\left( t \right) = 2 \Leftrightarrow \left[ \begin{array}{l} t = {t_1} \in \left( { – \infty {\mkern 1mu} ;{\mkern 1mu} – 1} \right)\\ t = 0\\ t = {t_2} \in \left( {1{\mkern 1mu} ;{\mkern 1mu} 2} \right) \end{array} \right.$Dựa vào bảng biến thiên của hàm số$t=\left| g\left( x \right) \right|=\left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right|$ ta có
+ Với $t={{t}_{1}}\in \left( -\infty \,;\,-1 \right)$ , phương trình $\left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right|={{t}_{1}}$ không có nghiệm ẩn $x$.
+ Với $t=0$, phương trình $\left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right|=0$ có 3 nghiệm ẩn $x$.
+ Với $t={{t}_{2}}\in \left( 1\,;\,2 \right)$, phương trình $\left| {{x}^{3}}-3{{\text{x}}^{2}}+2 \right|={{t}_{2}}$ có 6 nghiệm ẩn $x$.
Vậy phương trình đã cho có 9 nghiệm phân biệt.




0 Bình luận