Đề 003-TN THPT QG

Đề 003-TN THPT QG

Câu 49. Cho hình lăng trụ $ABC.{A}'{B}'{C}’$ có thể tích $V$, $I$ thuộc cạnh $C{C}’$ sao cho $CI=4I{C}’$. Gọi $M$, $N$ lần lượt là điểm đối xứng của ${A}’$, ${B}’$ qua $I$. Tính theo $V$ thể tích của khối đa diện $CABMN{C}’$.

A. $\frac{10}{3}V$.       

B. $\frac{9}{5}V$.       

C. $\frac{4}{3}V$.       

D. $\frac{8}{5}V$.

Hướng dẫn và Lời giải

Chọn C

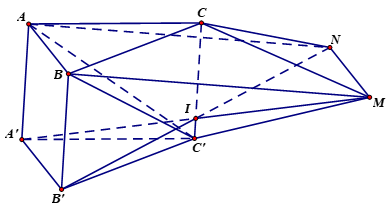
Ta có ${{V}_{CABMN{C}’}}={{V}_{{C}’CMN}}+{{V}_{{C}’CMB}}+{{V}_{{C}’CAB}}+{{V}_{{C}’CAN}}$

Dễ thấy: ${{V}_{{C}’CAB}}=\frac{1}{3}V$.

Do $I$là trung điểm ${A}’M$ nên $d\left( M\,;\,\left( BC{C}’ \right) \right)=d\left( A\,;\,\left( BC{C}’ \right) \right)$, nên

${{V}_{{C}’CMB}}=\frac{1}{3}d\left( M\,;\,\left( BC{C}’ \right) \right).{{S}_{BC{C}’}}$$=\frac{1}{3}d\left( {A}’\,;\,\left( BC{C}’ \right) \right).{{S}_{BC{C}’}}$$=\frac{1}{3}d\left( A\,;\,\left( BC{C}’ \right) \right).{{S}_{BC{C}’}}$$={{V}_{ABC{C}’}}=\frac{1}{3}V$

Tương tự: ${{V}_{{C}’CAN}}=\frac{1}{3}V$

Do tính đối xứng, ta có $\Delta I{A}'{B}’=\Delta IMN$

${{V}_{{C}’CMN}}={{V}_{{C}’IMN}}+{{V}_{CIMN}}=\frac{1}{3}d\left( {C}’\,;\,\left( IMN \right) \right).{{S}_{IMN}}+\frac{1}{3}d\left( C\,;\,\left( IMN \right) \right).{{S}_{IMN}}$

$=\frac{1}{3}d\left( {C}’\,;\,\left( I{A}'{B}’ \right) \right).{{S}_{I{A}'{B}’}}+\frac{1}{3}d\left( C\,;\,\left( I{A}'{B}’ \right) \right).{{S}_{I{A}'{B}’}}$

$={{V}_{{C}’I{A}'{B}’}}+{{V}_{CI{A}'{B}’}}={{V}_{C{A}'{B}'{C}’}}=\frac{1}{3}V$

Vậy ${{V}_{CABMN{C}’}}={{V}_{{C}’CMN}}+{{V}_{{C}’CMB}}+{{V}_{{C}’CAB}}+{{V}_{{C}’CAN}}=\frac{4}{3}V$.

Trở về đề thi