Giá trị lượng giác của một góc từ ${0^0} \to {180^0}$

GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KỲ từ ${0^0} \to {180^0}$

1. Định nghĩa

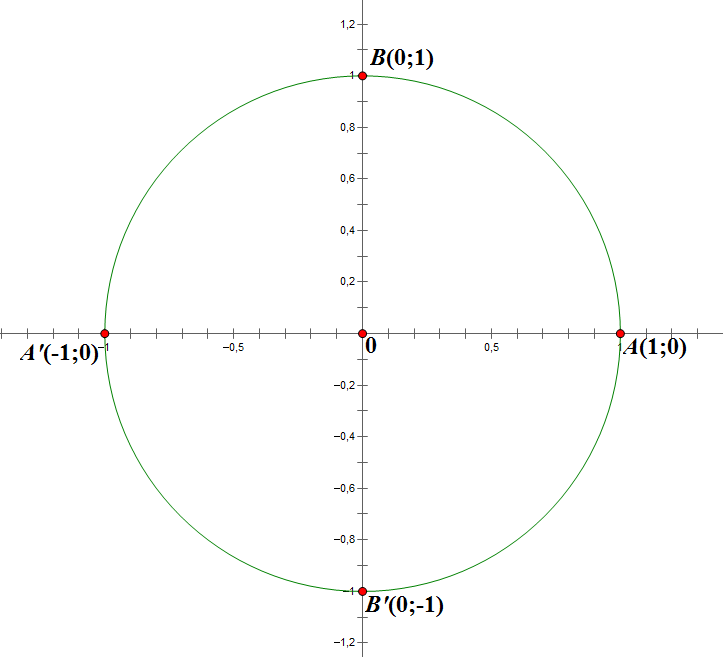
Định nghĩa 1. Đường tròn lượng giác.

Là đường tròn tâm trùng gốc tọa độ, Bán kính R=1; Cắt trục 0x tại A(1;0):A'(-1;0), cắt trục 0y tại B(0;1); B'(0;-1).

Định nghĩa 2. Giá trị lượng giác của một góc lượng giác.

Lấy M trên đường tròn đơn vị tâm O. Xét góc $\widehat {AOM} = \alpha $

. Giả sử M(x; y).

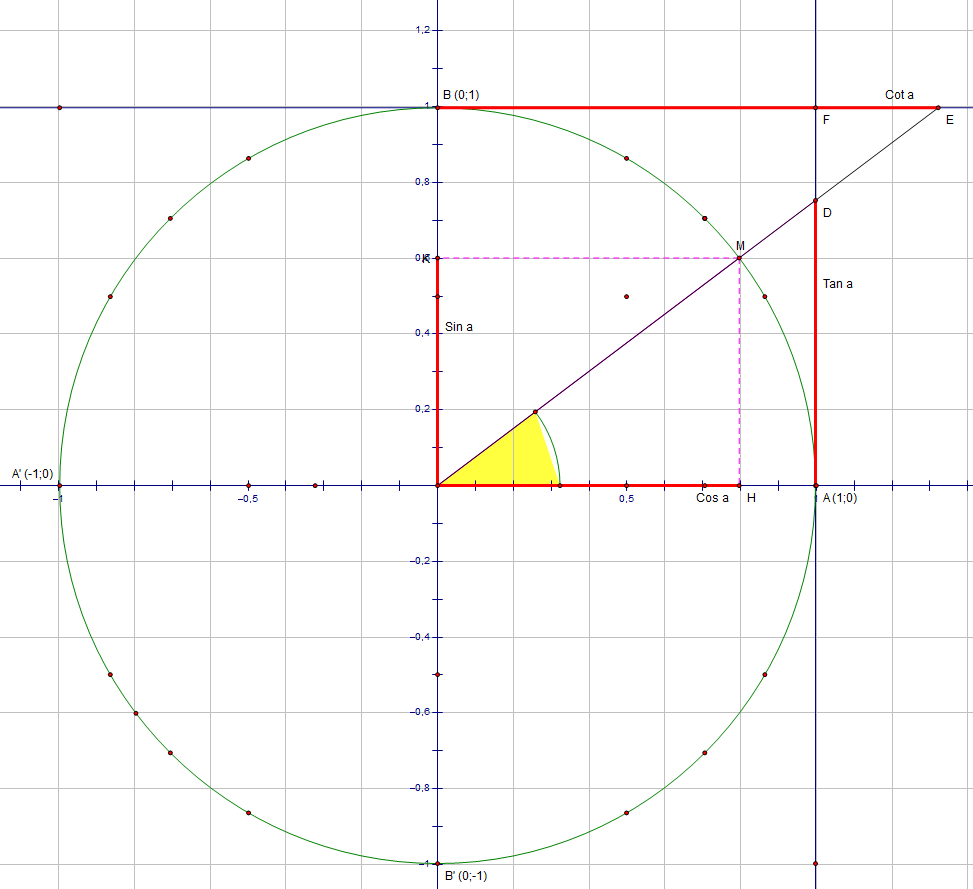
Khi đó: 

• $y = \sin \alpha $
• $x = \cos \alpha $
• $\frac{y}{x} = \tan \alpha $
• $\frac{x}{y} = \cot \alpha $

2. Các tính chất 

Tính chất 1. Điều kiện xác định của tan và cot.

• $\tan \alpha $ xác định khi và chỉ khi $a \ne {90^0}$.
• $\cot \alpha $ xác định khi và chỉ khi $\alpha \ne {90^0}$ v $a \ne {180^0}$ .

Tính chất 2. Dấu của giá trị lượng giác 

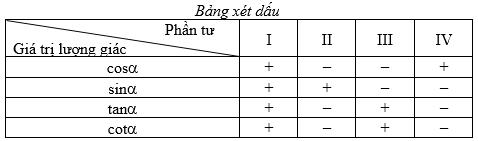
Tính chất 3. Sự tăng, giảm của các giá trị lượng giác

Tính chất 4. Giá trị của các góc đặc biệt từ ${0^0} \to {180^0}$

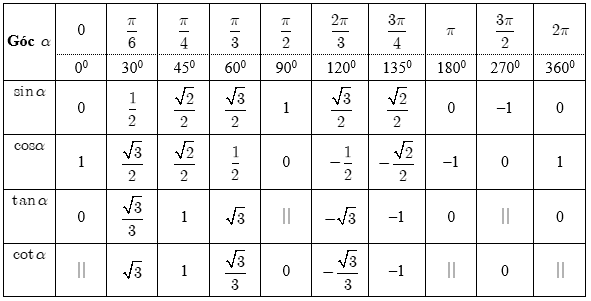
Tính chất 5. Trục tan $\alpha $ và trục cot $\alpha $

* Qua A, dựng At // 0x. Qua B dựng Bm//0x.

+ Ta có: $\frac{{\overline {MH} }}{{\overline {AD} }} = \frac{{\overline {OH} }}{{\overline {OA} }} \Leftrightarrow \frac{{\overline {OK} }}{{\overline {AD} }} = \frac{{\overline {OH} }}{{\overline {OA} }} \Leftrightarrow \overline {AD} = \frac{{\overline {OK} .\overline {OA} }}{{\overline {OH} }} = \frac{{y.1}}{x} = \tan \alpha $.

+Ta có:  $\frac{{\overline {MK} }}{{\overline {BE} }} = \frac{{\overline {OK} }}{{\overline {OB} }} \Leftrightarrow \frac{{\overline {OH} }}{{\overline {BE} }} = \frac{{\overline {OK} }}{{\overline {OA} }} \Leftrightarrow \overline {BE} = \frac{{\overline {OH} .\overline {OA} }}{{\overline {OK} }} = \frac{{x.1}}{y} = \cot \alpha $.

Từ đó:

+ Ox: Gọi là trục cosin;

+ 0y: gọi là trục sin.

+ At: gọi là trục tan.

+ Bm: Gọi là trục cot.

Tính chất 6. Hệ thức lượng giác cơ bản

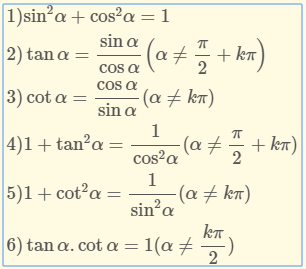
Chứng minh:

1. Ta có: ${y^2} + {x^2} = {(\overline {OK} )^2} + {(\overline {OH} )^2} = {\left( {\overline {OM} } \right)^2} = 1$ 

          $ \Leftrightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1$ (đpcm).

       2. $1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha + {{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}$.

Tương tự cho cac công thức còn lại.

Tính chất 7. Tương quan của các góc có liên quan đặc biệt.

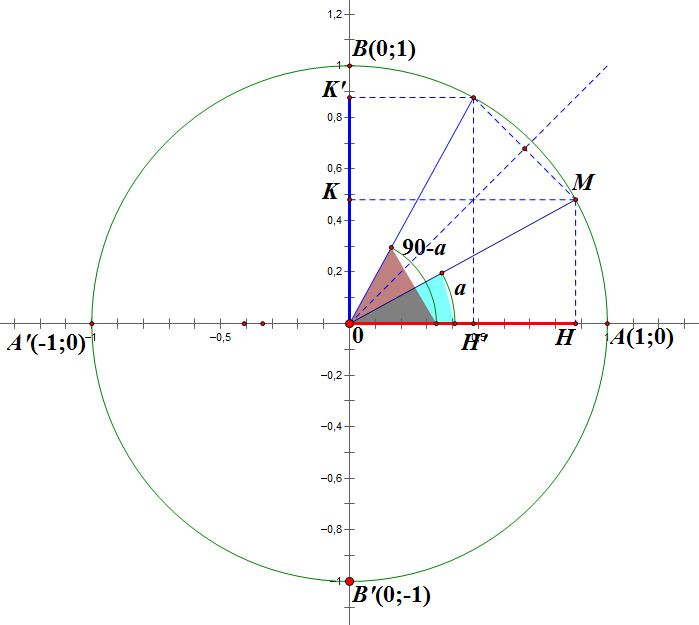
a) Góc phụ nhau:  a  và 90⁰ – a

• sin(90⁰ – a) = cosa
• cos(90⁰ – a) = sina 
• tan(90⁰ – a) = cota  
• cot(90⁰ – a) = tana    

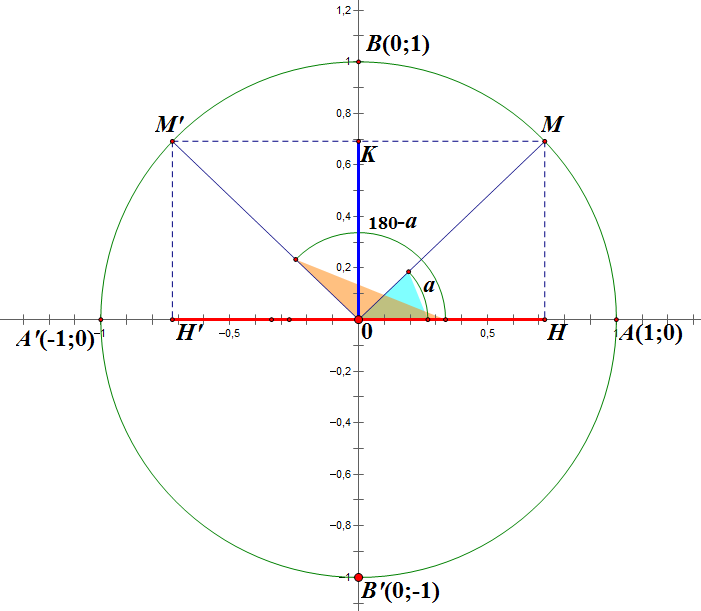
b) Góc bù nhau: α và 180⁰-α

• sin (180⁰ – a) = sin a
•   cos (180⁰ – a) = – cos a
•    tan (180⁰ – a) = – tan a
•    cot (90⁰ – a) = – cot a

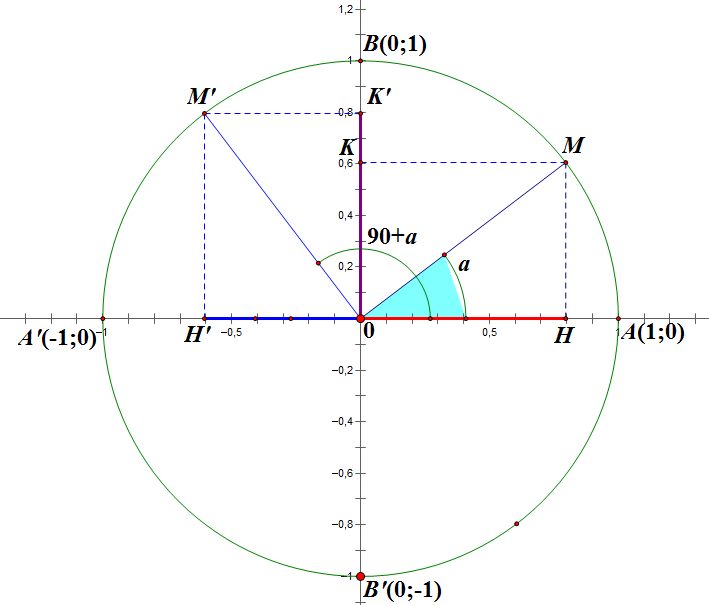
c) Góc hơn kém nhau 90⁰: α; và 90⁰+α

• sin (90⁰ + a) = cos a
• cos(90⁰ + a) = – sin a
•  tan(90⁰ + a) = – cot a
• cot(90⁰ + a) = – tan a

Tính chất 8. Miền giá trị

• $ – 1 \le \sin \alpha \le 1$
• $ – 1 \le \cos \alpha \le 1$
• $ – \infty < \tan \alpha < + \infty $
• $ – \infty < \cot \alpha < + \infty $.

Tóm lại

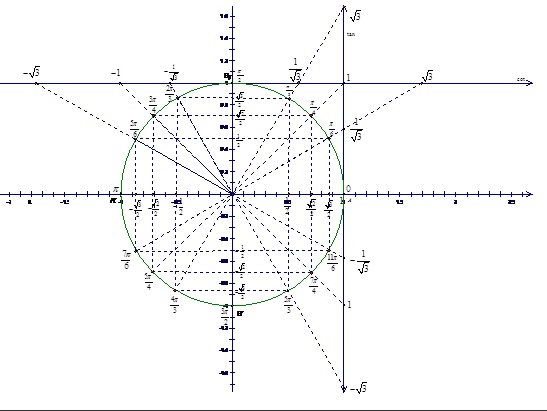
4. BÀI TẬP MẪU         

Bài 1. Tính giá trị các biểu thức sau:

a). asin0⁰ + bcos0⁰ + csin90⁰.     

b). acos90⁰ + bsin90 + csin180⁰.

c). a²sin90⁰ + b²cos90⁰ + c²cos180⁰.

d). 3  – sin²90⁰ + 2cos²60⁰ – 3tan²45⁰.

e). 4a²sin²45⁰ – 3(atan45⁰)² + (2acos45⁰)².

Bài 2.  CMR trong tam gic ABC ta có:

a). sinA = sin(B+C);                    b). cosA = – cos(B+C)

Bài 3. CMR:

a). sin105⁰ = sin75⁰                  

b). cos170⁰= – cos10⁰

c). cos122⁰ = – cos58⁰

Bài 4. Tính giá trị của các biểu thức sau:

a). sinx + cosx khi x bằng 0⁰; 45⁰; 60⁰.

b). 2sinx + cos2x khi x bằng 45⁰; 30⁰.

Bài 5. Cho biết một giá trị lượng giác của một góc, tính các giá trị lượng giác còn lại:

a) cho $sina = \frac{1}{3}$. Tính $\cos a;\tan a;\cot a$.

b) Cho $\tan a = \frac{4}{5}$. Tính: $\cot a;cosa;sina$

Bài 6. (B5 –SGK HH12) Cho góc x, với cosx=1/3. Tính giá trị của biểu thức:

P = 3 sin²x + cos²x.

Bài 7. Tìm miền giá trị của biểu thức:

$a)A = 2 – {\cos ^2}a$.

$b)B = \sqrt {1 + 3{{\cos }^2}a} $.

Bài 8. Không dùng máy tính, So sánh:

a)$\sin {88^0}28’36.28”$ và $\sin {88^0}28’36.29”$.

b) $\cos {88^0}28’36.37”$ và $\cos {88^0}28’36.38”$.

BÀI TẬP ĐỀ NGHỊ

 Bài 2. Chứng minh các đẳng thức sau:

a. (sinx + cosx)² = 1 + 2sinx.cosx

b. sin⁴x + cos⁴x = 1 – 2sin²x.cos²x.

c. tan²x – sin²x = tan²x.sin²x.

d. sin⁶x + cos⁶x = 1 – 3sin²x.cos²x

 Bài 3. Đơn giản các biểu thức sau:

  a. cosy + siny.tany

  b. sin(90⁰ – x) + cos(180⁰ – x) + sin²x(1 + tan²x) – tan²x.

Bài 4. Cho góc x nhọn với cosx = 1/4, Tính các giá trị lượng giác của các góc x.

———————————

Xem thêm:

• Giá trị lượng giác của góc từ 0⁰ đến 180⁰ .
• Góc giữa hai vec tơ.
• Tích vô hướng của hai véc tơ và ứng dụng.
• Hệ thức lượng trong tam giác.
• Giải tam giác.