Củng cố lý thuyết qua sơ đồ tư duy
Hệ thức lượng trong tam giác
1.Hệ thức lượng trong tam giác vuông
Cho tam giác ABC vuông tại A, có đường cao AH=h, BC=a, CA=b,, AB=c. Gọi BH=c’, CH=c’. Ta luôn có:
Các hệ thức về cạnh
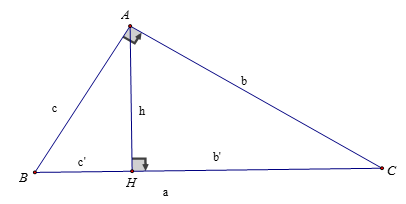
- ${a^2} = {b^2} + {c^2}$
- ${b^2} = a.b’$
- ${c^2} = a.c’$
- ${h^2} = b’.c’$
- $\frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}$
Các hệ thức về góc
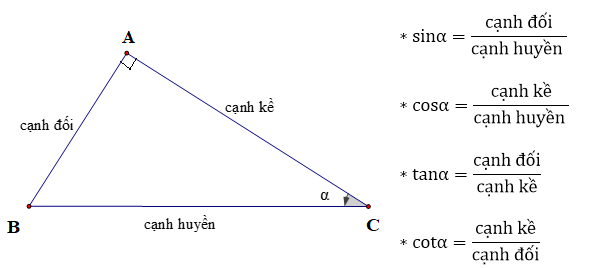
- $\sin B = \cos C = \frac{b}{a}$
- $\sin C = \cos B = \frac{c}{a}$
- $\tan C = \cot B = \frac{c}{b}$
- $\tan B = \cot C = \frac{b}{c}$
Hệ quả:
- $\tan B.\cot B = 1$
- ${\sin ^2}B + {\cos ^2}B = 1$
- $\tan B = \frac{{\sin B}}{{\cos B}}$
- $\cot B = \frac{{\cos B}}{{\sin B}}$
2. Hệ thức lượng trong tam giác thường
2.1.Định lý cosin.
Trong tam giác ABC bất kỳ với AC=b, BC=a,CA=b ta có:
- ${a^2} = {b^2} + {c^2} – 2bc\cos A$
- ${b^2} = {a^2} + {c^2} – 2ac\cos B$
- ${c^2} = {a^2} + {b^2} – 2ab\cos C$
Chứng minh
$\begin{array}{l}
{a^2} = {\left| {\overrightarrow {BC} } \right|^2} = {\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right)^2}\\
= {\overrightarrow {AC} ^2} – 2\overrightarrow {AC} \overrightarrow {AB} + {\overrightarrow {AB} ^2}\\
= {\overrightarrow {AC} ^2} + {\overrightarrow {AB} ^2} – 2\left| {\overrightarrow {AC} } \right|\left| {\overrightarrow {AB} } \right|\cos A\\
= {b^2} + {c^2} – 2bc\cos A
\end{array}$
Hệ quả:
- $\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}$
- $\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}$
- $\cos C = \frac{{{a^2} + {b^2} – {a^2}}}{{2ab}}$
Ví dụ
Cho tam giác ABC, có AC=10, BC=16 và C=1100 . Tính cạnh AB và góc A, B của tam giác.
Giải
Áp dụng định lý cosin , ta có:
$\begin{array}{l}
A{B^2} = C{A^2} + C{B^2} – 2CA.CB.\cos C\\
= {10^2} + {16^2} – 2.10.16.\cos {110^0}\\
= 465,44\\
\Rightarrow AB \simeq 21,6
\end{array}$
$\begin{array}{l}
\cos A = \frac{{A{C^2} + A{B^2} – B{C^2}}}{{2AC.AB}} = \frac{{{{10}^2} + 21,{6^2} – {{16}^2}}}{{2.10.(21,6)}} \simeq 0,718\\
\Rightarrow A \simeq {44^0}2′,B = {180^0} – (A + C) \simeq {25^0}58′
\end{array}$
2.2.Định lý sin
Cho tam giác ABC với BC=a, CA=b, AB=c và R là bán kính đường tròn ngoại tiếp, ta luôn có:
$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$
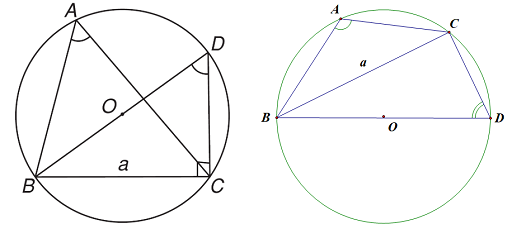
Chứng minh
Ta chứng minh: $\frac{a}{{\sin A}} = 2R$
- Nếu A nhọn (hình vẽ), ta có: tam giác BCD vuông tại C nên BC=BD.sinD hay a=2R.sinD. vì $\widehat A = \widehat D$ (góc nội tiếp cùng chắn một cung BC). Do đó:$a = 2R.\sin A$ hay $\frac{a}{{\sin A}} = 2R$ (đpcm).
- Nếu góc A tù, ta có sinD=sin(1800-A) suy ra: BC=BD.sinD hay $\frac{a}{{\sin A}} = 2R$ (đpcm)
Ví dụ
Cho tam giác ABC có B=200 , C=310 , AC=210. Tính góc A, AB, CB và R.
Giải
ta có: A=1800 -(200 +310 )=1290 .
Theo định lý sin:
$\begin{array}{l}
a = BC = \frac{{AC.\sin A}}{{\sin B}} = \frac{{210.\sin {{129}^0}}}{{\sin {{20}^0}}} \simeq 477,2\\
c = AB = \frac{{AC.\sin C}}{{\sin B}} = \frac{{210.\sin {{31}^0}}}{{\sin {{20}^0}}} \simeq 316,2\\
R = \frac{{BC}}{{2\sin A}} = \frac{{477,2}}{{2.\sin {{129}^0}}} \simeq 307,02
\end{array}$
2.3.Công thức diện tích tam giác
cho tam giác ABC có các cạnh BC=a, AB=c, AC=b. ha , hb , hc lần lượt là đường cao xuất phát từ đỉnh A,B,C. R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác và $p = \frac{{a + b + c}}{2}$ là nửa chu vi. Ta luôn có:
- ${S_{\Delta ABC}} = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}$
- ${S_{\Delta ABC}} = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B$
- ${S_{\Delta ABC}} = \frac{{abc}}{{4R}}$
- ${S_{\Delta ABC}} = \sqrt {p(p – a)(p – b)(p – c)} $ (công thức Hê rông)
- ${S_{\Delta ABC}} = pr$
Ví dụ
Tam giác ABC có a=13, b=14, c=15.
a)Tính diện tích tam giác.
b)Tính R,r.
Giải
a) Ta có: $p = \frac{{a + b + c}}{2} = \frac{1}{2}(13 + 14 + 15) = 21$. theo Hê rông ta có: ${S_{\Delta ABC}} = \sqrt {21(21 – 13)(21 – 14)(21 – 15)} = 84$.
b) Áp dụng: S=pr ta có: $r = \frac{S}{p} = \frac{{84}}{{21}} = 4$; $S = \frac{{abc}}{{4R}}$ suy ra: $R = \frac{{abc}}{{4S}} = \frac{{13.14.15}}{{4.84}} = 8,125$.
2.4.Công thức đường trung tuyến
Cho tam giác ABC có AB=c, AB=c, BC=a. Gọi ma , mb , mc lần lượt là độ dài các đường trung tuyến kẻ từ đỉnh A, B,C. Ta luôn có:
- ${m_a}^2 = \frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4}$
- ${m_b}^2 = \frac{{{a^2} + {c^2}}}{2} – \frac{{{b^2}}}{4}$
- ${m_c}^2 = \frac{{{a^2} + {b^2}}}{2} – \frac{{{c^2}}}{4}$
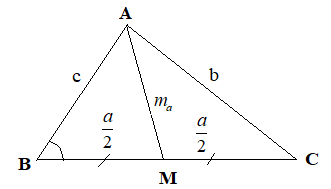
Chứng minh
Ta có: $\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}$ do đó:
$\begin{array}{l}
{m_a}^2 = {c^2} + {\left( {\frac{a}{2}} \right)^2} – 2c.\frac{a}{2}\cos B\\
= {c^2} + \frac{{{a^2}}}{4} – ac.\frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}\\
= \frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4}
\end{array}$
Ví dụ
Cho tam giác ABC có BC=7, AC=8, AB=6. Tính độ dài trung tuyến ma .
Giải
Ta có: $\begin{array}{l}
{m_a}^2 = \frac{{A{C^2} + A{B^2}}}{2} – \frac{{B{C^2}}}{4}\\
= \frac{{{8^2} + {6^2}}}{2} – \frac{{{7^2}}}{4} = \frac{{151}}{4}\\
\Rightarrow {m_a} = \frac{{\sqrt {151} }}{2}
\end{array}$
Luyện tập
Câu 1: Cho tam giác ABC có AB = 4, AC = 6, góc A = 120o. Độ dài cạnh BC là:
A. $\sqrt {19} $
B. $2\sqrt {19} $
C. $3\sqrt {19} $
D. $3\sqrt {19} $
Câu 2: Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Giá trị cos A bằng
A. 0,125
B. 0,25
C. 0,5
D. 0,0125
Câu 3: Cho tam giác ABC có a = 3, b = 5, c = 6. Giá trị của mc bằng
A. $\sqrt 2 $
B. $2\sqrt 2 $
C. 3
D. $\sqrt {10} $
Câu 4: Cho tam giác ABC có AB = 10, AC = 12, góc A = 150o.Diện tích của tam giác ABC bằng
A. 60
B. 30
C. $60\sqrt 3 $
D. $30\sqrt 3 $
Câu 5: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp của tam giác ABC bằng
A. 4
B. 3
C. 2
D. 1
Câu 6: Cho tam giác ABC có a = 5, b = 6, c = 7. Diện tích của tam giác ABC bằng
A. $12\sqrt 6 $
B. $3\sqrt 6 $
C. $6\sqrt 6 $
D. $9\sqrt 6 $
Câu 7: Cho tam giác ABC có a = 5, b = 12, c = 13. Bán kính đường tròn ngoại tiếp R của tam giác bằng
A. 13
B. 26
C. 6,5
D. 7,5
Câu 8: Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Câu 9: Cho tam giác ABC có a2 =b2 + c2 – bc. Số đo của góc A là
A. 135o
B. 150o
C. 60o
D. 120o
Câu 10: Cho tam giác ABC có a2 =b2 + c2 + $\sqrt 2 $.bc. Số đo của góc A là
A. 135o
B. 45o
C. 120o
D. 150o
Xem thêm:
0 Bình luận