Lý thuyết về giới hạn của hàm số.
A. Giới hạn hữu hạn tại điểm
1.Định nghĩa
a)Ví dụ mở đầu: Xét hàm số: $f(x) = \frac{{{x^2} – 1}}{{x – 1}}.$
- Tại x=1 thì f(1) không xác định.
- Cho x tiến tới 1, các số liệu thu được ở bảng sau:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | Không xác định | 2.001 | 2.010 | 2.100 |
Ta thấy, f(x) có thể gần 2 một cách tùy ý, chỉ cần cho x đủ gần 1.
Vậy: Ta nói f(x) tiến tới 2 khi x tiến dần tới 1, kí hiệu: $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 1}}{{x – 1}} = 2$
2. Định nghĩa
+) Cho khoảng \(K\) chứa điểm \(x_0\) và hàm số \(y = f(x)\) xác định trên \(K\) hoặc trên \(K\backslash {\rm{\{ }}{x_0}{\rm{\} }}\).
\(\underset{x\rightarrow x_{_{0}}}{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n ∈ K\backslash {\rm{\{ }}{x_0}{\rm{\} }}\) và \(x_n\rightarrow x_0\), ta có: \(\lim f(x_n) =L\).
3. Các giới hạn đặc biệt
a) \(\underset{x\rightarrow x_{_{0}}}{\lim} x = x_0\);
b) \(\underset{x\rightarrow x_{_{0}}}{\lim}c = c\);
4. Định lí về giới hạn hữu hạn
Định lí 1.
a) Nếu \(\underset{x\rightarrow x_{_{0}}}{lim} = L\) và \(\underset{x\rightarrow x_{_{0}}}{lim}\) \(g(x) = M\) thì:
\(\underset{x\rightarrow x_{_{0}}}{lim} [f(x) + g(x)] = L + M\);
\(\underset{x\rightarrow x_{_{0}}}{lim} [f(x) – g(x) = L – M\);
\(\underset{x\rightarrow x_{_{0}}}{lim} [f(x) . g(x)] = L.M\);
\(\underset{x\rightarrow x_{_{0}}}{lim}\) \(\frac{f(x)}{g(x)}\)= \(\frac{L}{M}\) (nếu \(M ≠ 0\)).
b) Nếu \(f(x) ≥ 0\) và \(\underset{x\rightarrow x_{_{0}}}{\lim} f(x) = L\), thì \(L ≥ 0\) và \(\underset{x\rightarrow x_{_{0}}}{\lim}\sqrt {f(x)} = \sqrt L\)
3. Giới hạn một bên
a) Ví dụ mở đầu:
Xét hàm số: $f(x) = \frac{{{x^2} – 1}}{{x – 1}}.$
- Tại x=1 thì f(1) không xác định.
- Cho x tiến tới 1, với các giá trị x <1, các số liệu (màu đỏ) thu được ở bảng sau:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | Không xác định | 2.001 | 2.010 | 2.100 |
Ta thấy, f(x) có thể gần 2 một cách tùy ý, chỉ cần cho x<1 và x đủ gần 1.
Vậy: Ta nói f(x) tiến tới 2 khi x tiến dần tới bên trái điểm 1, kí hiệu: $\mathop {\lim }\limits_{x \to {1^ – }} \frac{{{x^2} – 1}}{{x – 1}} = 2$
- Tương tự, cho x tiến tới 1, với các giá trị x >1, các số liệu (màu đỏ) thu được ở bảng sau:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | Không xác định | 2.001 | 2.010 | 2.100 |
Ta thấy, f(x) có thể gần 2 một cách tùy ý, chỉ cần cho x>1 và x đủ gần 1.
Vậy: Ta nói f(x) tiến tới 2 khi x tiến dần tới bên phải điểm 1, kí hiệu: $\mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} – 1}}{{x – 1}} = 2$
b) Định nghĩa giới hạn bên phải tại điểm x0
+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((x_0; b)\).
\(\underset{x\rightarrow x_{_{0}}^{+}}{\lim} f(x) = L\) khi và chỉ khi dãy số \((xn) bất kì, \(x_0<x_n< b\) và \(x_n\rightarrow x_0\),ta có \(\lim f(x_n) = L\).
c) Định nghĩa giới hạn bên trái tại điểm x0
+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; x_0)\).
\(\underset{x\rightarrow x_{_{0}}^{-}}{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(a <x_n< x_0\) và \(x_n\rightarrow x_0\), ta có
\(\lim f(x_n) = L\).
d) Định lý về giới hạn kẹp
Nếu: $\left\{ {\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to x_0^ + } f(x) = L}\\
{\mathop {\lim }\limits_{x \to x_0^ – } f(x) = L}
\end{array}} \right. \Rightarrow \mathop {\lim }\limits_{x \to x_0^{}} f(x) = L$
B. Giới hạn tại vô cực
a) Ví dụ mở đầu
Xét hàm số: $f(x) = \frac{1}{{x – 1}}.$
- Cho x tiến tới 1, với các giá trị x <1, các số liệu (màu đỏ) thu được ở bảng sau:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| –10 | –100 | –1000 | Không xác định | 2.001 | 2.010 | 2.100 |
Ta thấy, f(x) có thể gần $ – \infty $ một cách tùy ý, chỉ cần cho x<1 và x đủ gần 1.
Vậy: Ta nói f(x) tiến tới $ + \infty $ khi x tiến dần tới bên trái điểm 1, kí hiệu: $\mathop {\lim }\limits_{x \to {1^ – }} \frac{1}{{x – 1}} = – \infty $
Tương tự ta có: $\mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x – 1}} = + \infty $
b) Định nghĩa
+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; +∞)\).
\(\underset{x\rightarrow+\infty }{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n> a\), \(x_n\rightarrow +\infty\) thì \(lim f(x_n) = L\).
+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((-∞; a)\).
\(\underset{x\rightarrow-\infty }{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n< a\), \(x_n\rightarrow -\infty\) thì \(\lim f(x_n) = L\).
- $\mathop {\lim }\limits_{x \to x_0^ + } f(x) = + \infty ;\mathop {\lim }\limits_{x \to x_0^ + } f(x) = – \infty $
- $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty ;\mathop {\lim }\limits_{x \to – \infty } f(x) = – \infty $
Một số giới hạn đặc biệt
- \(\underset{x\rightarrow+\infty }{\lim} x^k= +∞\), với \(k\) nguyên dương.
- \(\underset{x\rightarrow-\infty }{lim} x^k= -∞\), nếu \(k\) là số lẻ.
- \(\underset{x\rightarrow-\infty }{lim}x^k = +∞\) , nếu \(k\) là số chẵn.
C. Các quy tắc tính giới hạn hàm số
1. Quy tắc giới hạn của tích \(f(x).g(x)\)
+ Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \pm \infty \) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = L \ne 0\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right).g\left( x \right)} \right]\) được cho trong bảng sau:
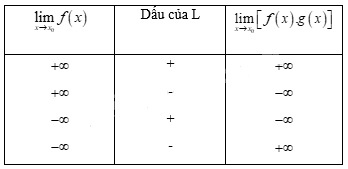
2. Quy tắc tìm giới hạn của thương \(\dfrac{f(x)}{g(x)}\)
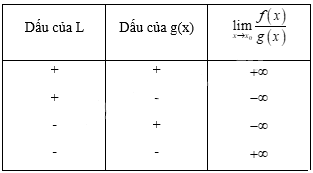
+ Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L \ne 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\) và \(g\left( x \right) > 0\) hoặc \(g\left( x \right) < 0\) với mọi \(x \in J\backslash \left\{ {{x_0}} \right\}\), trong đó \(J\) là một khoảng nào đó chứa \({x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) được cho trong bảng sau:
Củng cố lý thuyết bằng sơ đồ tư duy nhé.
Download sơ đồ tư duy:
D. Cách tính giới hạn hàm số thường gặp
1.Dạng $\frac{0}{0}$ đối với giới hạn tại một điểm
Ví dụ 1:
Tính: $\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 16}}{{x – 4}}$
Giải
Bước 1: Ta thế 4 vào phương trình f(x) thì sẽ được dạng nên khẳng định đây là dạng $\frac{0}{0}$.
Bước 2: Biến đổi: $\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 16}}{{x – 4}}$ $ = \mathop {\lim }\limits_{x \to 4} \frac{{\left( {x – 4} \right)\left( {x + 4} \right)}}{{x – 4}}$ $ = \mathop {\lim }\limits_{x \to 4} \left( {x + 4} \right) = 8$
Ví dụ 2.
Tính $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 1} – 1}}{{{x^2}}}$
Giải
Bước 1: Ta thế 0 vào biểu thức dưới dấu lim thì sẽ thấy dạng $\frac{0}{0}$ nên khẳng định đây là dạng $\frac{0}{0}$.
Bước 2: Lúc này ta biến đổi nó bằng cách nhân lượng liên hợp cho cả tử và mẫu:
$\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + 1} – 1}}{{{x^2}}}$ $ = \lim \frac{{\left( {\sqrt {{x^2} + 1} – 1} \right)\left( {\sqrt {{x^2} + 1} + 1} \right)}}{{{x^2}\left( {\sqrt {{x^2} + 1} + 1} \right)}}$ $\mathop { = \lim }\limits_{x \to 0} \frac{{{x^2}}}{{{x^2}\left( {\sqrt {{x^2} + 1} + 1} \right)}}$
Đến đây, chia cả tử và mẫu cho x2 ta được: $ = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt {{x^2} + 1} + 1}} = \frac{1}{2}$
2.Dạng $\frac{\infty }{\infty }$
Phương pháp: Ta chia cho x với số mũ lớn nhất của tử và mẫu.
Ví dụ 1.
Tính giới hạn sau: $\mathop {\lim }\limits_{x \to + \infty } \frac{{4{x^2} – x – 1}}{{3 + 2{x^2}}}$.
Giải
Thay $ + \infty $ và biểu thức ta thấy có dạng $\frac{{ + \infty }}{{ + \infty }}$.
Lại có bậc của x lớn nhất bằng 2, ta chia cả tử và mẫu cho x2.
$\mathop {\lim }\limits_{x \to + \infty } \frac{{4{x^2} – x – 1}}{{3 + 2{x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{4 – \frac{1}{x} – \frac{1}{{{x^2}}}}}{{\frac{3}{{{x^2}}} + 2}} = \frac{4}{2} = 2$
3. Dạng ${ + \infty + \infty }$
Ví dụ
Tính các giới hạn sau: $\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$
Giải
$\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{\left| x \right|\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – x\sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{x\left( { – \sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} – 1} \right)}}{{x -1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – \sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} – 1}}{{1 – \frac{1}{x}}} = \frac{{ – 3}}{1} = – 3$.
Lưu ý:
1. Học sinh rất dễ nhầm dạng ${ + \infty + \infty }$ và dạng ${ + \infty – \infty }$.
2. Nếu các em không tinh ý mà vận dụng phép ngay phép liên hợp thì lời giải sẽ dài hơn và dễ mắc sai lầm như sau:
Ta có: $\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {4{x^2} – x – 1} – x}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{\left( {\sqrt {4{x^2} – x – 1} – x} \right)\left( {\sqrt {4{x^2} – x – 1} + x} \right)}}{{\left( {x – 1} \right)\left( {\sqrt {4{x^2} – x – 1} + x} \right)}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{(4{x^2} – x – 1) – {x^2}}}{{\left( {x – 1} \right)\left( {\sqrt {4{x^2} – x – 1} + x} \right)}}$ $ = \mathop {\lim }\limits_{x \to – \infty } \frac{{3{x^2} – x – 1}}{{\left( {x – 1} \right)\left( {\sqrt {4{x^2} – x – 1} + x} \right)}}$
Đến đây ta chia phân phối cả tử và mẫu cho ${{x^2}}$. Ta được:
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{3 – \frac{1}{x} – \frac{1}{{{x^2}}}}}{{\left( {1 – \frac{1}{x}} \right)\left( { – \sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} + 1} \right)}} = \frac{3}{{1.( – 2 + 1)}} = – 3$
3. Sai lầm thường gặp.
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{3 – \frac{1}{x} – \frac{1}{{{x^2}}}}}{{\left( {1 – \frac{1}{x}} \right)\left( {\sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} + 1} \right)}} = \frac{3}{{1.(2 + 1)}} = 1$ => Kết quả sai.
Nguyên nhân sai lầm là khi đưa vào trong căn thì ta phải chú ý rằng: vì $x \to – \infty $ suy ra $x < 0$ => $\left| x \right| = – \sqrt {{x^2}} $.
Do đó: $\sqrt {4{x^2} – x – 1} = – \sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} $.
Một sai lầm thường gặp nữa, mặc dù có chú ý đến $x \to – \infty $ suy ra $x < 0$ => $\left| x \right| = – \sqrt {{x^2}} $ nhưng khi thực hiện lại sai vị trí dấu “-” như sau:
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{3 – \frac{1}{x} – \frac{1}{{{x^2}}}}}{{ – \left( {1 – \frac{1}{x}} \right)\left( {\sqrt {4 – \frac{1}{x} – \frac{1}{{{x^2}}}} + 1} \right)}} = \frac{3}{{ – 1.(2 + 1)}} = – 1$ => kết quả sai.
Trên đây là một số sai lầm rất đáng tiếc. Do vậy các em phải thật sự chú ý!!!
4. Dạng ${ + \infty – \infty }$
Ví dụ
Tính gới hạn sau:$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right)$.
Giải
Bước 1: Nhân với biểu thức liên hợp của biểu thức sau dấu lim.
Bước 2: Sau liên hợp, có dạng $\frac{\infty }{\infty }$, nên ta chia cả tử và mẫu cho x.
$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right)$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {\sqrt {{x^2} – x} – \sqrt {{x^2} + 1} } \right)\left( {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} } \right)}}{{\left( {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} } \right)}}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – x – 1}}{{\left( {\sqrt {{x^2} – x} + \sqrt {{x^2} + 1} } \right)}}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 1 – \frac{1}{x}}}{{\left( {\sqrt {1 – \frac{1}{x}} + \sqrt {1 + \frac{1}{{{x^2}}}} } \right)}} = – \frac{1}{2}$
6. Dạng ${0.\infty }$
Ví dụ
Tính giới hạn sau:$\mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\sqrt {\frac{x}{{{x^2} – 9}}} $
Giải
$\mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\sqrt {\frac{x}{{{x^2} – 9}}} $
$ = \mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\frac{{\sqrt x }}{{\sqrt {{x^2} – 9} }}$
$ = \mathop {\lim }\limits_{x \to {3^ + }} \left( {x – 3} \right)\frac{{\sqrt x }}{{\sqrt {x – 3} .\sqrt {x + 3} }}$
$ = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{\sqrt {x – 3} \sqrt x }}{{\sqrt {x + 3} }} = 0$
Chúc các bạn thành công!
Xem thêm:
- Các phương pháp tính giới hạn dãy số.
- Các phương pháp tính gới hạn hàm số.



0 Bình luận