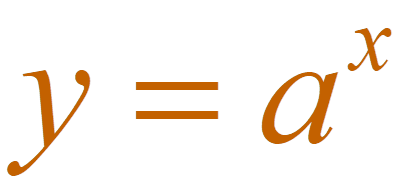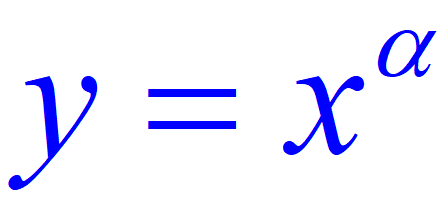LOGARIT I. Kiến thức cơ bản 1. Định nghĩa Cho số dương a \(a\ne1\) và số b dương. số thực α để aα= b được gọi là Logarit cơ số a của b và kí hiệu là logab, tức là: α=logab aα= b. Ví dụ: log10100=2 vì 102=100; log28=3 vì 23=8. Chú ý: Không có logarit của số 0 và số âm vì aα luôn dương với mọi α. Cơ Đọc tiếp…
Hàm số mũ I. Định nghĩa và tính chất của hàm mũ a) Định nghĩa hàm mũ Hàm số \(y=a^x\) (a > 0, a \(\ne\) 1)được gọi là hàm số mũ cơ số a. b) Đạo hàm của hàm số mũ \(\left(e^x\right)’=e^x\) \(\left(a^x\right)’=a^x.\ln a\) \(\left(a^u\right)’=u’.a^u.\ln a\) c) Tính chất khi a > 1 hàm số luôn đồng biến khi a < 1 hàm số luôn Đọc tiếp…
Hàm số lũy thừa I. Định nghĩa và tính chất • Định nghĩa: Hàm số \(y=f\left(x\right)=x^a\) được gọi là hàm số lũy thừa. Tập xác định: + nếu α là số nguyên dương. + nếu α nguyên âm hoặc bằng 0. + D=(0;+∞) với α không nguyên. • Đạo hàm : \(y’=a.x^{a-1}\). + Đạo hàm hàm hợp \(y=u^{\alpha}\) thì \(y=\alpha.u’.u^{\alpha-1}\)) • – Tính chất của hàm Đọc tiếp…
Lý thuyết: LŨY THỪA 1. Các định nghĩa. a) Lũy thừa với số mũ nguyên • Lũy thừa với số mũ nguyên dương : ${a^n} = \underbrace {a.a…a}_{{\rm{n -chu so a}}}$ (n thừa số a) (a ∈ R, n ∈ N* ). Trong đó: a gọi là cơ số, n gọi là số mũ,${a^n}$ gọi là: a lũy thừa n ( tuy nhiên ta hay gọi: a mũ n). • Đọc tiếp…
Lý thuyết hàm số: Khảo sát sự biến thiên và vẽ đồ thị hàm số I. Sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số (tổng quát) 1. Tập xác định. Tìm tập xác định của hàm số. 2. Sự biến thiên. + Tính đạo hàm y’ + Tìm các điểm xi tại đó y’ bằng 0 hoặc không xác định Đọc tiếp…
Lý thuyết hàm số: Đường Tiệm cận của đồ thị hàm số I. Tiệm cận 1. Định nghĩa tiệm cận ngang Đường thẳng \(y=y_0\) được gọi là đường tiệm cận ngang của đồ thị hàm số \(y=f\left(x\right)\) nếu \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=y_0\) hoặc \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=y_0\) 2. Định nghĩa tiệm cận đứng Đường thẳng \(x=x_0\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y=f\left(x\right)\) nếu một trong các điều Đọc tiếp…
Lý thuyết hàm số: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số (GTLN-GTNN). I. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số Định nghĩa: Giả sử hàm số \(f\) xác định trên tập hợp D. Khi đó : • $M = \mathop {Max}\limits_D f\left( x \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {f\left( x \right) \le M,x \in D}\\ {\exists {x_0} \in D:M = f\left( {{x_0}} Đọc tiếp…
Lý thuyết hàm số: CỰC TRỊ CỦA HÀM SỐ I. Cực đại, cực tiểu Định nghĩa cực đại, cực tiểu: Giả sử hàm số \(y=f\left(x\right)\) xác định và liên tục trên khoảng (a; b). Điểm \(x_0\in (a;b)\) và có đạo hàm y’ trên (a; \(x_0\)), ( \(x_0\); b). Khi đó: • Nếu \(f’\left(x\right)< 0\), ∀x ∈ (a; \(x_0\)) và \(f’\left(x\right)>0\), ∀x ∈ ( \(x_0\); b) thì hàm số \(y=f\left(x\right)\) đạt cực Đọc tiếp…