Phương pháp chứng minh hai mặt phẳng vuông góc

Phương pháp chứng minh hai mặt phẳng vuông góc

I. Định lý

Hai mặt phẳng được gọi là vuông góc với nhau nếu mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

II. Phương pháp chứng minh hai mặt phẳng vuông góc

Phương pháp 1. Phương pháp định nghĩa

$\left\{ \begin{align}
& d\subset (\alpha ) \\
& d\bot (\beta ) \\
\end{align} \right.\Leftrightarrow (\alpha )\bot (\beta )$

Ví dụ 1.

Cho hình chóp S.ABC có SA vuông góc đáy, tam giác đáy có AC=2a, SA=AB=a; BC=$a\sqrt{3}$. Chứng minh rằng (ABC) vuông góc với (SAB).

Giải

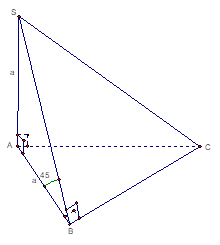
Xét tam giác ABC có: $A{B^2} = {(2a)^2} = A{B^2} + B{C^2} = {a^2} + {\left( {a\sqrt 3 } \right)^2}$. Suy ra tam giác ABC vuông tại B.

Mặt khác, ta có:

$\left. {\begin{array}{*{20}{c}}
{SA \bot (ABC) \Rightarrow SA \bot BC}\\
{BC \bot AB}\\
{SA \cap AB = \left\{ A \right\}}
\end{array}} \right\} \Rightarrow \left. {\begin{array}{*{20}{c}}
{BC \bot (SAB)}\\
{BC \subset (ABC)}
\end{array}} \right\} \Rightarrow (ABC) \bot (SAB)$

Ví dụ 2

Cho hình chóp S.ABCD, đáy ABCD là hình vuông tâm O, SA=SB=SC=SD=AB=a. CMR:    (SAC) $ \bot $ (ABCD); (SBD)$ \bot $(ABCD).

Giải

a). Tao có:

$\left. {\begin{array}{*{20}{c}}
{SA = SC}\\
{OA = OC}
\end{array}} \right\} \Rightarrow SO \bot AC(1)$

$\left. {\begin{array}{*{20}{c}}
{SB = SD}\\
{OB = OD}
\end{array}} \right\} \Rightarrow SO \bot BD(2)$

$ \Rightarrow SO \bot (ABCD)$

Do $SO \subset (SAC) \Rightarrow (SAC) \bot (ABCD)$

Tương tự: $SO \subset (SBD) \Rightarrow (SBD) \bot (ABCD)$.

Ví dụ 3.

Cho hình chóp S.ABC có SA vuông góc đáy, tam giác đáy có AC=2a, SA=AB=a; BC=$a\sqrt{3}$. Gọi H là trung điểm SB, M là trung điểm AC, K là trung điểm AM.

1. CMR:    (AHC) ^ (SBC).
2. CMR:   (SKB) và (SAC).

Giải

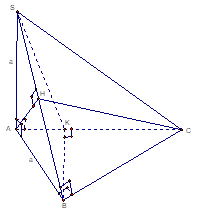
Theo Pita go, tam giác ABC vuông tại B.
$\begin{array}{l}
SA \bot (ABC) \Rightarrow SA \bot BC\\
Có BC \bot AB\\
\Rightarrow BC \bot (SAB)\\
AH \subset (SAB) \Rightarrow BC \bot AH\\
Do tam giác SAB cân tại A, H là trung điểm SB nên AH \bot SB\\
= > AH \bot (SBC)\\
Do AH \subset (AHC) \Rightarrow (AHC) \bot (SBC)
\end{array}$

2. Tương tự, ta có $BK \bot (SAC)$

mặt khác : $BK \subset (SBK) \Rightarrow (SBK) \bot (ASC)$.

Phương pháp 2: Góc giữa hai mặt phẳng cắt nhau bằng 90⁰

Ví dụ 1

Cho tứ diện S.ABC, SA=SB=2a, Tam giác ABC đều cạnh a, SC=$\frac{{3a\sqrt 2 }}{2}$. CMR (SAB)$ \bot $(ABC)

Giải

Gọi D là trung điểm AB. Do tam giác SAB cân tại S nên SD$ \bot $AB.

Do tam giác ABC đều suy ra CD$ \bot $AB.

Vậy : $\widehat {\left( {(SAB),(ABC)} \right)} = \widehat {SDC} = \alpha $

Ta có: $SD = \sqrt {S{A^2} – A{D^2}} = \sqrt {{{\left( {2a} \right)}^2} – {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt {15} }}{2}$.

Ta lại có: $CD = \frac{{a\sqrt 3 }}{2}$.

Xét tam giác SDC có:

$S{C^2} = S{D^2} + C{D^2} = {\left( {\frac{{a\sqrt {15} }}{2}} \right)^2} + {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = {\left( {\frac{{3a\sqrt 2 }}{2}} \right)^2}$

Suy ra tam giác SDC vuông tại D, suy ra (SAB)$ \bot $(ABC).

Phương pháp 3. Phương pháp vec tơ

Xem them phần: phương pháp tọa độ trong không gian

III. Bài tập thực hành

Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết SO$ \bot $(ABCD, SO=$a\sqrt 3 $ và đường tròn ngoại tiếp đáy có bán kính bằng $a\sqrt 2 $. Tính góc hợp bởi mặt bên và đáy?

A. ${30^0}$ B. ${45^0}$ C. ${60^0}$ D. ${75^0}$

Câu 2. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=AA’=a, AD=2a. Gọi $\alpha $ là góc giữa đường chéo A’C và đáy. Tính $\alpha $.

A. $\alpha = {20^0}45’$ B. $\alpha = {24^0}5’$

C. $\alpha = {30^0}18’$ D. $\alpha = {25^0}48’$

Câu 3. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng $\frac{{a\sqrt 2 }}{2}$ . Tính số đo góc hợp bởi mặt bên và đáy.

A. ${30^0}$ B. $ {45^0}$ C. ${60^0}$ D. ${75^0}$