Đề 003-TN THPT QG
Câu 47. Cho các số thực $a$, $b$ thỏa mãn ${{\text{e}}^{{{a}^{2}}+2{{b}^{2}}}}+{{\text{e}}^{ab}}\left( {{a}^{2}}-ab+{{b}^{2}}-1 \right)-{{\text{e}}^{1+ab+{{b}^{2}}}}=0$. Gọi $m$, $M$ lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức $P=\frac{1}{1+2ab}$. Khi đó, $m+M$ bằng
A. $\frac{10}{3}$.
B. $\frac{19}{5}$.
C. $\frac{7}{3}$.
D. $\frac{2}{5}$.
Hướng dẫn và Lời giải
Chọn A
Ta có: ${{\text{e}}^{{{a}^{2}}+2{{b}^{2}}}}+{{\text{e}}^{ab}}\left( {{a}^{2}}-ab+{{b}^{2}}-1 \right)-{{\text{e}}^{1+ab+{{b}^{2}}}}=0$$\Leftrightarrow {{\text{e}}^{{{a}^{2}}-ab+2{{b}^{2}}}}+{{a}^{2}}-ab+{{b}^{2}}-1-{{\text{e}}^{1+{{b}^{2}}}}=0$
$\Leftrightarrow {{\text{e}}^{{{a}^{2}}-ab+2{{b}^{2}}}}+{{a}^{2}}-ab+2{{b}^{2}}={{\text{e}}^{1+{{b}^{2}}}}+1+{{b}^{2}}$, $\left( * \right)$
Xét hàm số: $f\left( t \right)={{\text{e}}^{t}}+t$$\Rightarrow {f}’\left( t \right)={{\text{e}}^{t}}+1>0$$\Rightarrow $$f\left( t \right)={{\text{e}}^{t}}+t$ là hàm số đồng biến trên $\mathbb{R}$
$\left( * \right)\Leftrightarrow f\left( {{a}^{2}}-ab+2{{b}^{2}} \right)=f\left( 1+{{b}^{2}} \right)\Leftrightarrow {{a}^{2}}-ab+2{{b}^{2}}=1+{{b}^{2}}\Leftrightarrow {{a}^{2}}-ab+{{b}^{2}}=1$
Do đó: $P=\frac{1}{1+2ab}=\frac{{{a}^{2}}-ab+{{b}^{2}}}{{{a}^{2}}+ab+{{b}^{2}}}$
TH1: $b=0\Rightarrow P=1$
TH2: $b\ne 0\Rightarrow P=\frac{{{\left( \frac{a}{b} \right)}^{2}}-\left( \frac{a}{b} \right)+1}{{{\left( \frac{a}{b} \right)}^{2}}+\left( \frac{a}{b} \right)+1}=\frac{{{x}^{2}}-x+1}{{{x}^{2}}+x+1}=g\left( x \right)$ với $x=\frac{a}{b}$
${g}’\left( x \right)=\frac{2{{x}^{2}}-2}{{{\left( {{x}^{2}}+x+1 \right)}^{2}}}$;
$g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = – 1 \end{array} \right.$Bảng biến thiên
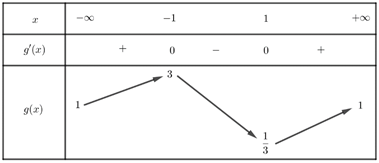
Do đó: $m={{P}_{\min }}=\frac{1}{3}$; $M={{P}_{\max }}=3$ $\Rightarrow m+M=\frac{10}{3}$.



0 Bình luận